Graphene is a kind of nano-material, which was first produced in 2004. As is well known, two-dimensional (2D) pristine graphene has a high in-plane mechanical strength due to its strong sp² C–C covalent bonds. This excellent mechanical property leads to its extensive applications in the mechanical and mechanical-electronic field.^[1–5] However, synthesized large-area graphene inevitably contains the grain boundaries (GBs), which play an important role in the stability of 2D graphene crystalline structure. Studying the GB effects on the graphene physical properties is one of fundamental interest. For example, some GBs in graphene have perfect electron transport properties,^[6,7] and heat rectification at the asymmetric grain boundaries in graphene is predicted theoretically.^[8]

The tilt grain boundaries also affect the graphene mechanical strength. As is well known, the stretching limit of a material depends not only on its intrinsic strength of the chemical bonds between two atoms,^[9] but also on the defects in it, such as the tilt grain boundaries. In 2010, Grantab et al.^[10] showed by the molecular dynamics (MD) simulation method that when the tilt GB density in graphene increases, its stretching limit also increases, violating the conventional consideration. This anomalous mechanical phenomenon arouses the great interest of a vast number of researchers working in the material science and condensed matter physics. Two years later, another research team supplemented that the tilt GB distribution in graphene also affects the material stretching limit,^[11] indicating that the stretching limit could increase or decrease, depending on the tilt angle of the armchair-oriented tilt GB. Following their work, many kinds of GBs, such as the zigzag-armchair-oriented ones with any tilt angle have been constructed in order to investigate the GB role in the stability of 2D graphene sheets.^[12–21] In particular, Zhang et al. studied graphene sheets with sinuous grain boundaries which showed improved mechanical behavior.^[22] The other 2D materials with grain boundaries have also been studied, e.g., metal dichalcogenides MX₂ (M = Mo, W; X = S, Se) with grain boundaries.^[23] Besides this, shear deformation on the GBs was also investigated theoretically.^[24] All of these studies predicted that when the graphene sheet with the GBs was stretched to a limit length, the stress was mainly loaded on the heptagon rings. As a result, the bonds lying on the heptagon usually break first, then lead to a crack, which was immediately proved by the following work.^[25] So in Ref. [21], the authors established a quasi-static strain model based on the bond breaking mechanism mentioned above to predict the final stretching failure of graphene sheet with grain boundary. However, all of these studies were carried out at room or low temperatures.

The temperature effects, especially the high-temperature effects, on elongation of graphene sheets with the GBs have not been discussed in detail, which cannot be ignored in practical applications as a real physical condition. Graphene must have intrinsic ripples to maintain its quasi 2D structure, while the temperature could affect the ripples in monolayer and bi-layer graphene.^[26] The polycrystalline graphenes are not flat due to the existence of GBs,^[11] which could also be affected by temperature. So in this work, we will pay attention to the temperature, especially the high-temperature effect on the mechanical properties of graphene with the GBs. We perform classic MD simulations to investigate the elongation process of graphene with the GBs at different temperatures. In particular, we will pay more attention to the GB behaviors in the stretching process at high temperature and the corresponding physical mechanism of them at high temperature and under large stress.

The rest of this paper is organized as follows. In Section 2, we will give our calculation method and MD simulation details. In Section 3, the MD results and discussion are presented. Finally, in Section 4, we give the summary and conclusions.

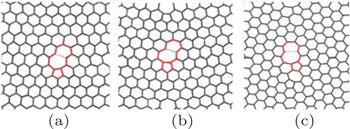
We use the software packages of Large-Scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) to perform the MD simulations. Following the GB definitions in Ref. [10], the GB geometric structures used in our work at two different tilt angles for the zigzag or armchair orientation are shown in Fig. 1.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Geometric structures of grain boundaries at different values of tilt angle θ: (a) 5.5° and (b) 13.2° in the zigzag-oriented graphenes, (c) 15.8° and (d) 28.7° in the armchair-oriented graphenes.

Each sample contains about 6000∼7000 atoms with its size being about 90 Å in width and 200 Å in length. A periodical condition is used along the GB’s direction. Adaptive intermolecular reactive empirical bond order (Airebo) potential is used to describe the interaction between carbon atoms, in which the smaller cutoff distancer_cc is chosen to be 1.92 Å to follow what was used in Refs. [10] and [11]. Before we perform the MD simulations, each sample is relaxed using the MD method. The stretching direction is perpendicular to the grain boundary, and the stretching velocity is set to be 0.005% per picosecond, which follows the case in Refs. [10] and [11]. In the stretching process, the graphene sheet is allowed to shrink along the GB direction. All the MD simulations are performed using NVT ensemble.

The stress on a single carbon atom could be obtained by Virial stress expression.^[27,28] Once the stress value on each carbon atom is calculated, we average it over the whole sample every 0.5 ps in the second half of the total relaxation time of 5 ps in order to obtain the stress of the entire system as also used in Refs. [10] and [11].

The graphene sheets with different grain boundaries are stretched at different temperatures until a crack occurs. As an example, the stretching curves at different temperatures for two different GBs shown in Fig. 1 are given in Fig. 2. For comparison, the ultimate stress of a pristine graphene sheet stretched in its armchair direction at 300 K is shown using the red dashed line in Fig. 2, whose value is about 98.5 GPa. It is found from Fig. 2 that at a temperature of 300 K, the zigzag-oriented GBs (ZZ-GBs) at tilt angle θ = 5.5° and 13.2° could be stretched to 11% and 13.5% longer, respectively. Their ultimate strengths are found to reach 68.2 GPa and 79.3 GPa, respectively. On the other hand, at the same 300 K, the armchair-oriented GBs (AC-GBs) at tilt angle θ = 15.8° and 28.7° are found to be stretched to 8% and 18% longer, respectively, and their maximum strengths reach 54.4 GPa and 91.2 GPa, respectively. These results are in agreement with those mentioned in Ref. [10].

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Stress–strain curves of graphene sheets with different grain boundaries: the zigzag-oriented GBs at tilt angles of (a) 5.5° and (b) 13.2° the armchair-oriented GBs at tilt angles of (c) 15.8° and (d) 28.7°. The red dashed line indicates the ultimate stress of pristine graphene stretched in armchair direction at 300 K.

The geometric structures of the graphene sheets with different GBs just before the sample cracking at room temperature are shown in Fig. 3. It is found from Fig. 3 that for both the ZZ- and AC-GBs, the bonds lying on the GB heptagon ring and marked by dotted lines in Fig. 3, are broken, leading to the appearance of a hollow defect around the heptagon rings. It is simply these hollow defects that lead finally to a crack on different samples at room temperature. Previous studies^[12,13] explained that the bonds on heptagon rings contain the initial inner strain, which determines the failure strength. Our MD simulation results at a temperature of 300 K are consistent with the results in Refs. [12] and [13].

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Geometric structures of graphenes with different GBs before their cracks at temperature of 300 K: the zigzag-oriented GBs at tilt angles of (a) 5.5° and (b) 13.2° (c) the armchair-oriented GB at a tilt angle of 15.8°. The defects form due to the bonds’ breaking marked with dotted lines.

From Fig. 2, it is clearly seen that when the temperature increases, the sample ultimate stress decreases. For example, in Fig. 2(a), the ultimate strength of graphene with the ZZ-GB at a tilt angle of 5.5° is 68.2 GPa at 300 K, which decreases to 48.5 GPa when the temperature increases to 1000 K. In Fig. 2(b), the maximum strength of graphene with the ZZ-GB at a tilt angle of 13.2° falls from 79.3 GPa to 40.83 GPa when temperature increases from 300 K to 1000 K.

Furthermore, we study the graphene sheet with mixed type GBs, namely, composed of both ZZ-GB and AC-GB. Figure 4(a) shows the structure of the mixed type GBs, in which the blue colored 5–7 defects constitute the ZZ-GB at a tilt angle of 13.2° and the red colored 5–7-defect line indicates the AC-GB at a tilt angle of 15.8°. Figure 4(b) gives the sample stress–strain curves at different temperatures, the stretching direction is marked with a red arrow in Fig. 4(a). It is seen that the ultimate stress of the sample with mixed type GB also decreases with temperature increasing. We find that during the elongation the bond shared by hexagon and heptagon rings in blue 5–7 defects breaks first, then the bond shared by hexagon and heptagon rings in red 5–7 defects breaks, finally leading to the sample cracking.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. (a) The graphene sheet with mixed-type GBs. The blue GBs are zigzag-oriented, and red ones are armchair-oriented. The red arrow indicates the stretching direction. (b) The stress–strain curves of graphene sheet with mixed-type GBs at different temperature.

We give the relationships between the ultimate stresses of pristine graphene sheets and ones with various kinds of GBs at different temperatures in Fig. 5. It could be seen from Fig. 5 that the ultimate stresses of all samples decrease with temperature increasing, which are independent of GB type (ZZ- or AC-GB) and mismatch angle. However, by comparing Fig. 5(a) with Fig. 5(b), it is clearly seen that there is still a difference between the variation behaviors of the ultimate stresses of graphene sheets with the ZZ- and AC-GBs.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Plots of ultimate stress versus temperature for graphenes with (a) zigzag-oriented GBs, (b) armchair-oriented GBs at different mismatch angles, in which the orange triangle indicates the pristine graphene sheet ultimate stress at different temperatures when it stretches along the armchair direction.

As is well known, for the samples with AC-GBs, their ultimate stresses increase with their tilt angles at zero temperature, which is almost kept at different temperatures, even at very high 1000 K. But, for the ZZ-GBs, although their varying behaviors of ultimate stresses with their tilt angles at the lower temperatures, e.g., less than 600 K, can keep the same as those of them at T = 0, when T further increases up to higher than 600 K, the situation will become different because the dropping of the velocity of the ultimate stress ε_c with T increasing for the samples with a lower tilt angle of θ = 5.5° becomes lower than those of the samples with the higher tilt angles of 9.5° 13.2°, and 16.4° when the temperature is higher than about 700 K, which makes ε_c value at θ = 5.5° become larger than those at the larger tilt angles of 9.5°, 13.2°, and 16.4° when T > 700 K.

In order to know clearly the temperature effect on the mechanical properties of graphene sheets with various GBs at different mismatch angles, we study the relationships between ultimate stress and tilt angle at different temperatures. Our MD simulation results for both the zigzag- and armchair-oriented GBs are shown in Figs. 6(a) and 6(b), respectively. Figure 6(a) shows that the ultimate stress at tilt angle 16.4° sharply decreases at low temperature. We compare the sketch maps of ZZ-GBs at tilt angles 13.2° and 16.4° in Fig. 7.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Plots of ultimate stress versus tilt angle for (a) zigzag-oriented GBs and (b) armchair-oriented GBs at different temperatures.

The GB at 13.2° is composed of an array of uniformly distributed disclination dipoles, in which each dipole is a 5/7 defect; while at 16.4° the GB is composed of an array of disclination dipole cluster which is composed of two 5/7 defects. Reference [11] pointed out that the stress induced by disclination cluster is much greater than that by the disclination dipole. So the ultimate stress at tilt angle 16.4° is smaller than that at 13.2° showing a sharp decrease in the curve of ultimate stress with tilt angle increasing. Furthermore, it is seen clearly from Fig. 6 that both the ZZ- and AC-orientation GBs exhibit different temperature effects. For the zigzag-oriented GBs, it is seen from Fig. 6(a) that there exists a specific (or critical) tilt angle θ_c = 16.4° to separate the tilt angles into two different regions. For the larger tilt angle region (θ ≥ θ_c), the variation behaviors of ultimate stress with tilt angle at different temperatures are qualitatively the same as that at zero one^[11] except that all the ultimate stress values at each tilt angle decrease with temperature increasing. However, in the smaller tilt angle region (θ < θ_c), the variation behaviors of ultimate stress with tilt angle at different temperatures are very different from those in the larger θ region (≥ θ_c). But in the lower temperatures (T ≤ 600 K), the variation behaviors at different temperatures are also similar to that at the zero one,^[11] besides the fact that the ultimate stress values at all tilt angles become smaller when temperature increases. In the higher temperature region (between 800 K and 1000 K), the ultimate stress variation behavior with θ becomes different from (or even opposite to) those at T = 0 K and T ≤ 600 K, making the variation curve with θ evolve into concave at high T = 1000 K from the original convex at T = 0 K and T ≤ 600 K. That is to say, for the smaller tilt angles of θ ≤ 13.2° the ultimate stress value at high T = 1000 K decreases with the increase of θ, indicating that at high T, the mechanical behavior of graphene with ZZ-orientation GBs is recovered into the normal one, i.e., the ultimate stress value of the system decreases with the increase of the defect density, which is just opposite to the anomalous behavior at T = 0 and in lower T region (T ≤ 600 K).

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. Sketch maps of graphene sheets with zigzag-oriented GBs at (a) tilt angle of 13.2° and (b) 16.4°.

As explained in Refs. [10] and [11], the maximum initial inner strains in the bonds shared by the heptagon and hexagon rings in GBs of the samples with different tilt angles determine their final ultimate stresses. The larger the bond initial inner strain, the smaller the final ultimate stress is. As is well known, the C–C bond length in pristine graphene without an external strain is 1.42 Å. The topological defects (5/7 pairs) in the GBs of graphene would induce the initial inner strains of the C–C bonds in the sample, e.g., those shared by the heptagon and hexagon rings in GBs, which would be different at different mismatch angles. Following the definition in Ref. [12], the initial inner strain could be expressed by a relative C–C bond length of δL = L − L₀, where the L₀ = 1.42 Å and L is the mean value of the bond shared by the heptagon and hexagon rings. Therefore, the longer the δL, the larger the bond inner strain is. In order to investigate the temperature effect on the maximum initial inner strain in GBs, the mean values of the initial relative bond lengths δL for the ZZ-GBs at θ ≤ 16.4° are calculated at different temperatures without an applied strain and the obtained results are shown in Fig. 6. For comparison, the mean relative bond lengths at T = 0 K but different tilt angles are also given in Fig. 8, which are the same as those given in Ref. [11]. By comparing Fig. 6(a) with Fig. 8, it is clearly seen that when T < 800 K, the initial inner strain variations with tilt angles in the bonds shared by the heptagon and hexagon rings in the ZZ-GBs are qualitatively similar to each other, except that their initial inner strain values increase with T increasing, making the final ultimate stresses at different tilt angles decrease with T increasing as shown in Fig. 5(a). However, when T becomes larger than 800 K, the above variation situation becomes different at different tilt angles θ ≤ 16.4°. For example, the mean relative bond lengths of samples at θ = 9.5° and 13.2° increase faster than those at θ = 5.5° and 16.4° which makes the ultimate stress of the sample exhibit a minimum value at θ = 9.5° and T = 800 K. Finally, when T further increases up to 1000 K, the mean relative bond length variation with tilt angle increasing (θ ≤ 16.4°) becomes opposite to that at T = 0, as shown in Fig. 8. The mean relative bond length increases with θ, reaching its maximum value at θ = 13.2° and then decreases until θ = 16.4° which clearly explains the ultimate stress variation with tilt angle increasing (θ ≤ 16.4°) at T = 1000 K as shown in Fig. 6(a). That is the ultimate stress of the sample with the ZZ-GBs decreasing with θ increasing until θ = 13.2° and then increases until θ = 16.4° whose variation is just opposite to that of the initial inner strain with θ ≤ 16.4° at 0 K. On the other hand, as shown in Fig. 6(b), for the AC-oriented GBs, their ultimate stresses increase monotonically with increasing the tilt angle at all temperatures, which is similar to that at T = 0. That means the temperature variation has no big effect on the mechanical properties of the samples with AC-GBs except to reduce their ultimate stress values at different θ values.

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. Plots of mean relative C–C bond length δL versus tilt angle in a range of θ ≤ 16.4° for samples with ZZ-GBs at different temperatures. Here, δL = L − L0, where L0 = 1.42 Å, and L is the mean length of the C–C bond shared by heptagon and hexagon rings in ZZ-GBs.

Finally, we focus our attention on the temperature effect on GB per se. As the temperature increases, the structure of GB does not show obvious change. However, due to the existence of GB, the surface of the graphene sheet is not strictly flat (see Fig. 9(a)). There are ripples along the GB. We denote the height of the ripple as hz indicated in Fig. 9(b). Figure 9(c) shows that the height of the ripple in the graphene sheet with ZZ-GBs at tilt angle of 5.5° increases with temperature increasing. Specifically at T > 800 K, the hz increment speed becomes higher than that at low temperature.

Fig. 9.

	Figure Option ViewDownloadNew Window
	Fig. 9. (a) Sketch map of ripple in graphene sheet due to the existence of GBs. (b) The definition of ripple’s height due to the GBs. (c) The curve of ripple height versus temperature.

From our MD simulation results, it can be concluded that the finite temperature has large effects on mechanical properties of graphene sheets with various GBs. Firstly, the ultimate stresses for both samples with ZZ-, AC-orientation and mixed type GBs decrease with increase of temperature. Secondly, the initial inner strains on those C–C bonds shared by heptagon and hexagon rings in ZZ-GBs without an applied external strain exhibit different values, depending on temperature and also mismatch angle. It is just the values of the initial inner strains to be found that determine the final ultimate stresses of the sample with ZZ-GB at different temperatures, especially at higher T ≥ 800 K and smaller tilt angles θ ≤ 13.2° for the ZZ-GBs. In contrast, for the samples with AC-GBs, the finite temperatures are found to have only less effects on the system mechanical properties, making only the ultimate stress values at different tilt angles to decrease with increasing temperatures. Finally, the height of ripple induced by GB in graphene sheet becomes high when temperature rises.