Nowadays the realization and application of dispersion in an optical medium is a hot topic in the field of optical physics, and the research promotes the developments of physics, such as quantum electrodynamics, quantum optics, optical information processing and optical sensing.^[1–5] The early research on optical medium dispersion aimed to achieve fast light (the group velocity of light is greater than its phase velocity) or slow light (the group velocity of light is less than its phase velocity). In 1999, Hau et al. utilized the electromagnetically induced transparency (EIT) (proposed by Harris et al.^[1]) to realize strong normal dispersion in ultracold atoms and a light speed of 17 m/s.^[2] After that, researchers reported many methods of producing strong dispersion, such as coherent population oscillation, stimulated Brillouin scattering, and dual wave coupling.^[6–8] These methods produced strong dispersions mainly by using the interaction between medium and external light field.

On the other hand, with the development of the optical waveguide technology, strong dispersion could also be produced in an optical resonator structure.^[9–11] An optical resonator could be a fiber ring resonator, or Fabry–Perot resonator, or micro-ring/micro-disk resonator. The ordered arrangement of the optical resonators can form a variety of optical resonator structures with strong dispersion, such as coupled resonator optical waveguide (CROW),^[9] side-coupled spaced sequence of resonator (SCISSOR),^[10] and coupled resonator induced transparency (CRIT).^[11] In an optical resonator structure, the dispersion is induced by the mutual coupling and interference between the resonators, so it is determined by the parameters of the resonator structures and can be formed at any optical wavelength. Also, the structures are usually comprised of optical waveguide or fiber, and thus it is compatible with current optical devices. Therefore, the optical resonator structure can be used for filters,^[12,13] dispersion compensation,^[14–16] enhanced nonlinearity,^[17] and rotation sensing.^[18,19]

The EIT-like effect originates from the destructive interference of electromagnetic fields of different pathways. There are two main schemes for the generation of the EIT-like effects: near-field coupling^[20,21] and phase coupling.^[22–24] The near-field coupling scheme hinges on the strength of the coupling, whereas the phase coupling scheme depends on the phase of the coupling. The CRIT is proposed by Smith et al.^[11] Compared with other optical resonator structures, this structure is relatively simple, and can produce the electromagnetically induced-transparency-like effect due to the classical destructive interference of optical fields. In recent years, the CRIT has been widely investigated in optical image delay,^[25] wavelength division multiplexing,^[26] optical Fano resonance,^[27] optical bistability,^[28] and optical switching.^[29,30] In the present paper, using the advantages of high transmittance, simple structure, and flexibility in designing dispersion, we investigate the control of dispersion in the structure and obtain simultaneous normal and abnormal dispersion. The results are beneficial for applications of CRIT structure in optical signal processing and optical communication.

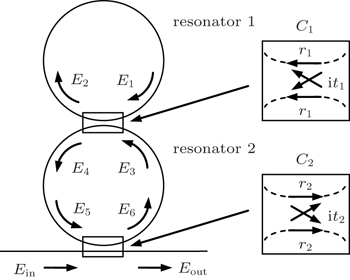
The CRIT structure shown in Fig. 1 consists of the input/output waveguide, two ring resonators and two couplers C₁ and C₂.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Schematic diagram of a CRIT structure.

Using the transfer matrix method,^[15,16] we can derive the transfer function of the structure

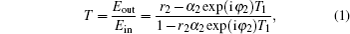
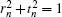
The q-th (q is a positive integer) order dispersion coefficient is

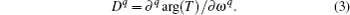
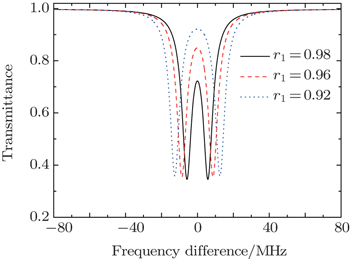
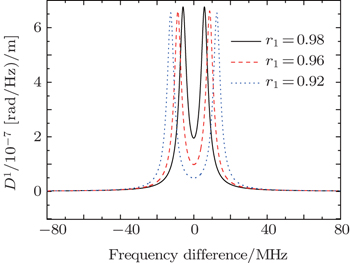
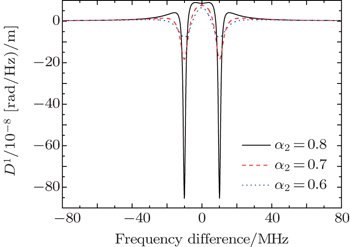
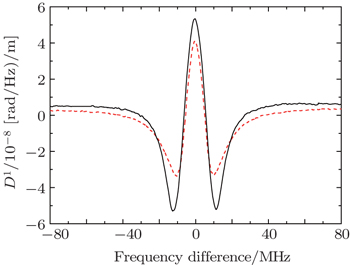
The optical characteristics of CRIT structure depend on structure parameters, such as the length of resonator, amplitude reflection coefficient and loss. The bandwidth of the structure is mainly determined by the length of resonator, and in general they are in inverse relation. Amplitude reflection coefficient affects the transmission spectrum, especially the dispersion bandwidth and the distribution of dispersion intensity. Figures 2 and 3 show the transmission spectra and dispersions of CRIT structures with different amplitude reflection coefficients, where n_e = 1.5, L₁ = L₂ = 1 m, r₂ = 0.85, α₁ = α₂ = 0.98. It can be seen that there are induced transparency phenomena in the transmission spectra, and the transmittance of the transparency peak and the corresponding dispersion intensity change with amplitude reflection coefficient. With the decrease of amplitude reflection coefficient, the transmittance of the transparency peak increases gradually; meanwhile, the dispersion bandwidth also increases. The two peaks in the dispersion curve are caused by the dramatic change of transmittance, so they correspond to the two low transmittance modes in the transmission spectrum. The distance between the two peaks is proportional to dispersion bandwidth. As shown in Fig. 3, the dispersion is normal (the first order dispersion coefficient is positive) in the dispersion bandwidth, whereas the dispersion is weak outside the dispersion bandwidth. When light frequency is far away from the dispersion bandwidth, the dispersion gradually approaches the waveguide dispersion.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Transmission spectra of CRIT structures with different amplitude reflection coefficients.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Dispersions of CRIT structures with different amplitude reflection coefficients.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Transmission spectra of CRIT structures with different amplitude attenuation factors.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Dispersions of CRIT structures with different amplitude attenuation factors.

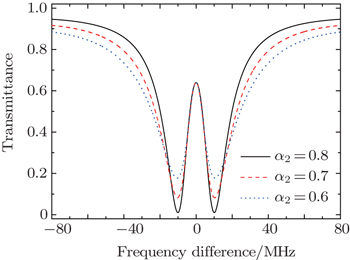
In the CRIT structure, adjusting loss is an effective method of controlling dispersion. Figures 4 and 5 show the transmission spectra and dispersions of CRIT structures with different amplitude attenuation factors, where n_e = 1.5, L₁ = L₂ = 1 m, r₁ = 0.95, r₂ = 0.8, and α₁ = 0.95. It can be seen that with the decrease of amplitude attenuation factor the transmittance decreases gradually. However, neither the transmittance of the transparency peak nor dispersion bandwidth is almost changed. The dispersion of the transparency peak is normal, and the dispersions of the two low transmittance modes in the transmission spectrum are abnormal. The transmittances of the two low transmittance modes increase with the decrease of amplitude attenuation factor, but their corresponding abnormal dispersion intensities decrease. It can also be seen that the loss has little effect on the transmission spectrum shape, but seriously affects the dispersion spectrum, especially the intensity of abnormal dispersion.

Figure 6 shows the experimental setup for measuring the dispersion of the CRIT structure comprised of fiber. The center wavelength of the polarized laser is 1550 nm, and the linewidth is less than 10 kHz. The function generator is used to linearly tune the laser frequency by applying a triangular wave voltage signal to the tunable laser. The PC is used to control the polarization state of the polarized laser in the fiber CRIT structure. After passing through the isolator and PC, the laser is equally divided into two beams by the first 3-dB coupler. Then the two beams pass through the structure and the other arm respectively, and finally are combined by another 3-dB coupler where the interference signal is detected by detector D2. Detector D1 is used to detect the transmission spectrum of the structure. The lengths of the two resonators comprised of single mode fiber (SMF-28) are both about 1 m, r₁ = (0.90)^1/2, and r₂ = (0.70)^1/2. The tunable attenuator is used to adjust the loss of the structure.

Fig. 6.

	Figure Option ViewDownloadNew Window
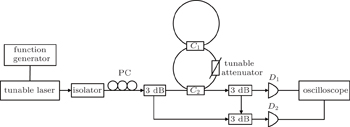	Fig. 6. Experimental setup for measuring dispersion of the fiber CRIT structure. D1 and D2 are two detectors. PC is the polarization controller.

Figures 7 and 8 show the experimental transmission spectra and dispersions of the fiber CRIT structure with different amplitude attenuation factors. It can be seen that there is an induced transparency phenomenon in the transmission spectrum and the full width at half maximum (FWHM) of the transparency peak is about 6 MHz. The transmittance of the transparency peak is about 0.69, and the transmittances of the two low transmittance modes are both about 0.32. In the dispersion bandwidth, there are simultaneous normal and abnormal dispersion. The transparency peak corresponds to the normal dispersion, and the two low transmittance modes belong to the abnormal dispersion. Outside the dispersion bandwidth, the dispersion is weak and approaches the waveguide dispersion. Therefore, we have realized the control of dispersion in the structure and obtain simultaneous normal and abnormal dispersion.

We can see that adjusting loss is an effective method of controlling dispersion in the CRIT structure. It should be noted that the loss usually reduces the transmittance of the structure. However, the transmittance also depends on the coherent effect between the two resonators. Therefore, if we choose approximate amplitude reflection coefficients of the two couplers, we can make up the decrease of transmittance due to loss.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. Experimental transmission spectra of the fiber CRIT structure with different amplitude attenuation factors.

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. Experimental dispersions of the fiber CRIT structure with different amplitude attenuation factors.

In this work, it is demonstrated that adjusting loss is an effective method of controlling dispersion in a CRIT structure. Meanwhile, simultaneous normal and abnormal dispersion can also be obtained by adjusting the loss. The transparency peak corresponds to normal dispersion, and the two low transmittance modes belong to abnormal dispersion. Although the loss usually reduces the transmittance of the structure, we can choose approximate amplitude reflection coefficients of the two couplers in advance to make up the decrease of transmittance due to loss.

The control of dispersion in the structure could be used in optical signal processing, such as wavelength division multiplexing and tunable optical signal delay. For example, optical signals with different center wavelengths have different group velocities due to strong normal and abnormal dispersion, so they could be distinguished in time domain. For a narrow linewidth pulse, we could tune its speed by adjusting the loss.