† Wei Zhu and Xiao Xiao contributed equally to the work.
‡ Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11222430, 11434011, 11475254, and 11175247) and the National Key Basic Research Program of China (Grant Nos. 2012CB922104 and 2014CB921202).
We study the single-photon scattering along a one-dimensional cavity array with two distant two-level atoms in a supercavity, which aims to simulate a recent x-ray experiment [Nature
Recently, some important experimental progress in x-ray quantum optics was made by Röhlsberger et al. in the group of Deutsches–Elektronen–Synchrotron.[1,2] In their experiments, the high-energy photons from an x-ray synchrotron radiation were injected into an effective cavity formed by two layers of Pt atoms. In this effective cavity there are one or two layers of 57Fe atoms. In the system with one layer of 57Fe atoms, the reflectivity of a single x-ray photon, as a function of the energy of this photon, has a single peak. The collective Lamb shift of the 57Fe can be detected from the position of this peak. Nevertheless, when there are two layers of 57Fe atoms, the following two interesting effects can appear.
The purpose of our research is to understand the physics of the above effects with some simple models, rather than the complicated analysis provided by Röhlsberger et al.[1,2] In their papers, the transmission matrix method with many external parameters is applied to obtain the reflected magnitude, which is compared with that from a three level EIT to get the physical explanation. However, the microscopic mechanism to explain the phenomena is not clear in their work, which motivates us to build a microscopic model without any external parameter to understand the basic physics in their settings.
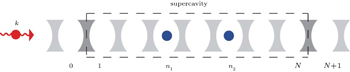
In our previous works[3,4] we have used the atom-array and cavity-array models to study the collective behaviors of the Fe atoms, as well as the effect of the cavity in the single-photon scattering on a single layer of 57Fe atom. In this paper, we use a one-dimensional (1D) cavity array model to study the physics of the single-photon scattering on an effective cavity with two layers of atoms. In our model the photon propagates in the 1D array of cavities. We further assume that there is one supercavity in that array, and two two-level atoms are coupled to the photon in this supercavity. Here we use the photon in the cavity array to simulate the x-ray photon in the experiment,[2] use the supercavity to simulate the effective cavity formed by the Pt atoms, and use each two-level atom to simulate one layer of Fe atoms.
We exactly calculate the single-photon reflectivity in this toy model. Our result shows that, when one atom is exactly at the node of an eigen-mode of the supercavity, there is almost no splitting of the peak of the reflectivity, i.e., the effect (i) cannot appear. Nevertheless, the atom at the node can change the positions of the reflectivity valleys. On the other hand, when the atom is shifted a little from the exact node, the effect (i) can appear, and effect (ii) can still not appear. We further explained these behaviors with an analysis with formal scattering theory. Our results show that, to completely explain the effects (i) and (ii) in the experiments, it is necessary to take into account the spontaneous emission of the atoms in the excited state, and the non-resonant modes of the supercavity in our problem.
The remaining part of this paper is organized in the following way. In Section 2 we introduce our model and calculate the single-photon reflectivity with exact numerical calculation. In Section 3 we explain our results with formal scattering theory. We draw our conclusions in Section 4. We show some details of our calculations in Appendix A.
We consider a one-dimensional (1D) single-mode cavity array with infinite length, which is shown in Fig.
In the rotated frame, the Hamiltonian of our system is given by


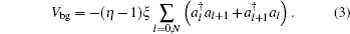

In the absence of the supercavity and the atom–photon coupling (i.e., η = 1 and Ω1 = Ω2 = 0), the eigen-state of a single photon with momentum k is

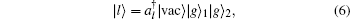
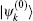

When η ≪ 1 and Ω1,2 ≠ 0, the photon will be scattered by the supercavity and the two atoms. In this paper we consider this single-photon scattering problem. The scattering state of a photon with incident momentum k can be expressed as follows:[4,5]
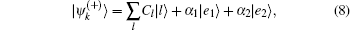


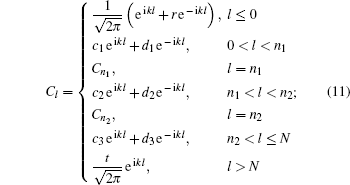

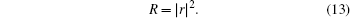
We numerically solve Eq. (
We also numerically investigate the system with two atoms in the supercavity. In Fig.
However, in our system the two-level atom at the node of the resonant mode obviously changes the positions of the peaks. As shown in Fig.
We also study the system where one atom is at the anti-node of the supercavity mode, and another atom is slightly shifted from the node. As shown in Fig.
In this section we provide a physical explanation for the splitting of the single-photon reflectivity in the case where the photon is coupled to both of the two atoms. We will show that this splitting can be understood as a result of the atom–photon-coupling-induced energy shifts and effective coupling of the two atoms. Although the following analysis is done for our mode in Section 2, it can be directly generalized to the system in the experiment[2] of the x-ray photon scattering.
Before going into the detail of the calculations, here we first give a qualitative physical picture for shift and splitting of the single-photon reflectivity. We consider the scattering of a single photon on a single two-level atom. We first focus on the case in which there is no supercavity and the photon is just moving in a simple 1D cavity array (i.e., the case with η = 1 and Ω2 = 0). In this case, if the atom is far-off resonant to the incident photon, then the photon cannot be influenced by the atom, and just goes across it. Thus, the single-photon reflectivity is almost zero. Nevertheless, if the atom is near-resonant to the photon, the atom can absorb the photon and re-emit it. Furthermore, when the photon is re-emitted, it can go along either the same or the opposite direction of movement of the incident photon. In the latter case, the photon is reflected by the atom. Therefore, the single-photon reflectivity |rA(k)|2 has a peak when the atom is near-resonant to the photon, i.e., when ωa = ωc + Ek or Δ = Ek.
In the system with a supercavity, when the atom in the supercavity absorbs the photon and re-emits it, the photon can stay in the supercavity for a long time, and thus will not become far away from the atom immediately. During that time, the photon can be re-absorbed by the atom and re-emitted again. As a result of this process, the effective energy of the atom can be shifted. That shift effect is just like the AC Stark effect. Furthermore, the single-photon reflectivity |rA(k)|2 peaks when the single photon energy is resonant to the effective energy of the atom. Thus, when the effective energy of the atom is shifted, the peak of the single-photon reflectivity is also shifted.
Now let us consider the system with two atoms 1 and 2. By absorbing a single photon, these two atoms can jump from the two-atom ground state |g〉1|g〉2 to the two-atom excited states |e〉1|g〉2 or |g〉1|e〉2. Furthermore, when there is a supercavity, then the incident photon can be absorbed by the 1st atom, and be re-emitted by this atom, and then be absorbed and re-emitted by the 2nd atom, and then be absorbed and re-emitted by the 1st atom again, …. Since the photon can stay in the supercavity for a long time, these processes can occur for many cycles. During these processes, the states |e〉1|g〉2 or |g〉1|e〉2, whose bare energies are the same, can be effectively coupled. As a result of this coupling, the degeneracy of these two states is destroyed and thus the effective energies of these two states becomes different. In addition, the single-photon reflectivity peaks when the photon is near resonant to the transition from |g〉1|g〉2 to |e〉1|g〉2 or |g〉1|e〉2. Therefore, there will be two peaks corresponding to the effective energy gap between |e〉1|g〉2 and |g〉1|g〉2 and the one between |g〉1|e〉2 and |g〉1|g〉2.
Now we illustrate the above picture with analytical calculations.
According to Eq. (


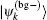
We first discuss the case where the photon is only coupled to atom 1, i.e., Ω2 = 0. In this case we have α2 = 0, and thus the reflection amplitude rA(k) contributed by the atom is determined by the parameter α1. This parameter can be calculated as follows. As shown in Appendix A, the scattering state 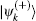

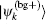
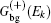

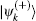

Substituting Eqs. (





Now we consider the case where the photon is coupled to both of the atoms. For simplicity, we assume Ω1 = Ω2 = Ω as shown in Eq. (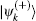



Substituting Eq. (



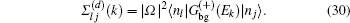
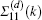

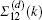


Now we use Eq. (

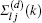

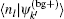



On the other hand, when both of the atoms are not set at the node of the eigen-mode of the supercavity, all the elements of the matrix-type Lamb shift Σ(d)(k), as well as the components of the vectors β±(k), are non-zero. In that case, the condition of the peak of R becomes Ek ≈ Re[Δ + λa] or Ek ≈ Re[Δ + λb], where λa,b are the two eigen-values of Σ(d)(k). In most of the cases we have λa ≠ λb. Therefore, the reflectivity R, has two splitting peaks.
We present a supercavity model based on one dimensional cavity array to simulate a recent x-ray experiment in Ref. [2]. Without introducing the dissipation, we find that for the system with one atom exactly at a node of the supercavity, there is no splitting of the reflectivity peak. That peak can only appear when the atom is slightly shifted from the node. This result shows that it is very difficult to use our model to explain the splitting of the reflectivity peak appearing in the node–antinode arrangement of the two layers of 56Fe atoms. However, we find that the appearance of the two-level atom at the node significantly changes the positions of the two reflectivity valleys, which implies that the non-resonant modes of the supercavity play an important role in the single photon scattering problem.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 |