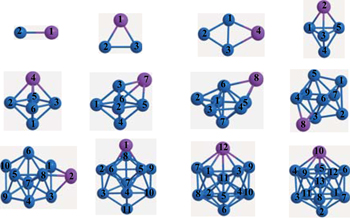
Using the computational scheme described in Section 2, we have explored a number of low lying isomers and determined the lowest energy structures of Fe_nAu clusters up to n = 12. The obtained ground state structures which include these isomers within 0.4 eV of the most stable structure are shown in Fig. 1, together with the symmetries, magnetic moment, and relative energy (ΔE). The point-group symmetry of each cluster is determined using a tolerance of 0.001 Å between the atomic position in the computed structure and the atomic position in the symmetrized reference structure. The lowest energy structures for pure Fe_n+1 clusters are also considered for comparison. The small Fe_n+1 clusters up to n = 12 are extensively investigated computationally by using DFT. In this work, the geometries for pure iron clusters obtained from the published literatures are reoptimized by using the spin-polarized DFT as described in Section 2. With few exceptions, our calculated structures for n ≤ 6 agree with published theoretical results,^[8–10,13] similar to recently predicted equilibrium structures.^[6,9] This reoptimization leads to a slight change in the geometry of the iron clusters. The values of average binding energy (E_b) and the average bond length (d) for the lowest energy structures of Fe_nAu clusters are calculated and listed in Table 2, where the corresponding values for Fe_n+1 clusters are given in the brackets.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Lowest-energy structures and low-lying isomers with different relative energies (in unit eV) of FenAu (n = 1−12) clusters. The ground state geometries of the corresponding bare Fen+1 clusters are also given on the left. The blue and pink balls represent Fe and Au, respectively. Distances are given in unit Å.

Table 2.

Table 2.

Table 2. Values of average binding energy (Eb), average bond length (d), average magnetic moment at Fe atom (ūatom), HOMO–LUMO (highest occupied molecular orbital–lowest unoccupied molecular orbital) gaps in the lowest energy structures of FenAu clusters. Corresponding values for Fen+1 cluster are given in the brackets. . Cluster Eb/(eV/atom) d/Å ūatom Gap/eV FeAu 1.552 (1.621) 2.398 (2.020) 3.040 (3.000) 0.040 Fe2Au 2.001 (2.089) 2.394 (2.271) 3.301 (3.333) 0.485 Fe3Au 2.433 (2.516) 2.366 (2.353) 3.010 (3.500) 0.506 Fe4Au 2.736 (2.848) 2.450 (2.398) 3.667 (3.600) 0.404 Fe5Au 2.970 (3.103) 2.450 (2.400) 3.341 (3.333) 0.376 Fe6Au 3.144 (3.252) 2.448 (2.391) 3.163 (3.143) 0.475 Fe7Au 3.251 (3.337) 2.446 (2.426) 3.000 (3.000) 0.452 Fe8Au 3.318 (3.387) 2.429 (2.393) 2.885 (2.889) 0.423 Fe9Au 3.395 (3.445) 2.455 (2.434) 2.980 (3.000) 0.393 Fe10Au 3.453 (3.516) 2.477 (2.454) 3.086 (3.091) 0.120 Fe11Au 3.521 (3.576) 2.484 (2.476) 2.983 (3.167) 0.204 Fe12Au 3.586 (3.657) 2.514 (2.504) 3.076 (3.385) 0.126

Table 2. Values of average binding energy (Eb), average bond length (d), average magnetic moment at Fe atom (ūatom), HOMO–LUMO (highest occupied molecular orbital–lowest unoccupied molecular orbital) gaps in the lowest energy structures of FenAu clusters. Corresponding values for Fen+1 cluster are given in the brackets. .

FeAu is C_∞v symmetry dimer, whose bond length and average binding energy are 2.398 Å and 1.552 eV/atom, respectively. These results lie between Fe₂ (2.020 Å, 1.621 eV/atom) and Au₂ (2.488 Å, 1.189 eV/atom). Compared with it of pure Fe₂ (6 μB), the magnetic moment of FeAu dimer is reduced by 3 μ_B. Our computed values are in good agreement with the values (2.470 Å and 3 μ_B) obtained in previous paper.^[39]

Energetically, the most favorable structure of the Fe₂Au cluster with a total magnetic moment of 7 μ_B is in the form of an isoscele triangle (C_2v), whose Fe–Fe distance is 2.073 Å. This may be seen as replacing an Fe atom with an Au atom. Our results about Fe₂Au are proved by Sun et al.,^[33] whose results show the Fe–Fe distance of 2.020 Å and the same magnetism (7 μ_B). Its metastable state shares the linear chain structure, and the third stable state (9 μ_B) is similar to the ground state. They are energetically less stable by 0.020 eV and 0.124 eV, respectively.

A planar structure (C_2v) is the most stable Fe₃Au cluster with 9 μ_B of total magnetic moment. The second energetically degenerate structure (9 μ_B), which is of a turnup rhombus (four atoms are not on the same plane) structure (C_s), is energetically less favorable than the most stable structure in energy by 0.062 eV. The third lowest-energy structure is similar to the most stable structure, but they differ by 11 μ_B of total magnetic moment. A distorted tetrahedronal configuration with C_s symmetry is the fourth stable isomer. The energy is 0.382 eV less stable in energy compared the lowest energy structure, which means that there is the turning from the planar (2D) structure to the three-dimensional (3D) structure.

In the case of Fe₅, we find the C_2v triangular bipyramid structure to have the lowest energy. For Fe₄Au, the overall structures are totally retained, but they are slightly distorted triangular bipyramid with the Au atom at the vertex. The most stable isomer is of C_s symmetry and it has a total magnetic moment of 15 μ_B, which is reduced by 3 μ_B in comparison with the pure Fe₅ (18 μ_B). By contrast, the second stable structure (C_s) with a total magnetic moment of 13 μ_B is 0.120 eV evidently higher in energy. The other two stable isomers (C_3v) have total magnetic moments of 15 μ_B and 13 μ_B, and 0.164 eV and 0.166 eV above the lowest-energy structure, respectively.

The C_2v configuration of Fe₅Au with the magnetism (17 μ_B) is found to be the most stable isomer, which may be viewed as a deviation from substitution of a Fe atom by an Au atom in the octahedron Fe₆ (D_4h) structure. The other distorted octahedron geometrical isomer with C_4v symmetry is considered to be the second stable structure at a slightly higher energy (0.037 eV). Differently, the following two stable isomers prefer to share a capped triangle bipyramid with Au atom being at the cap position, which are located at 0.094 eV and 0.286 eV in energy above the most stable conformation.

For the Fe₆Au clusters, we consider a lot of initial geometries including the bicapped triangular bipyramid, capped octahedron, pentagonal bipyamid, bicapped square pyramid, etc. At last, an Au-capped octahedron structure with C_s symmetry is found to have the lowest energy. However, the metastable state is a distorted pentagonal bipyramid (C_2v) with the impurity Au atom in the middle pentagonal ring plane, and is found to be only 0.091 eV less stable than the ground state. The third state also favors a capped octahedron (C_3v) and is energetically less favorable than the most stable structure by 0.137 eV. The fourth state is still a capped octahedron (C_s) with the Au atom at the square site, and is 0.382 eV higher in total energy. Moreover, we notice that these four stable structures of Fe₆Au have the equal total magnetic moment (19 μ_B).

Energetically the most favorable structure for Fe₇Au (21 μ_B) is an Au-capped distorted pentagonal bipyramid with C₁ symmetry. The metastable state with a classic bicapped octahedron structure is 0.134 eV in energy higher than the lowest-energy structure. As seen in Fig. 1, the third lowest-energy structure is still a bicapped octahedron with an Au atom at the vertex position of the octahedron. It has the same magnetism as the ground state structure and is 0.136 eV higher in energy. A capped-pentagon bipyramid (21 μ_B), where Au atom becomes a part of the pentagonal ring, is regarded as the fourth stable isomer and has a high relative energy of ΔE = 0.263 eV.

In the case of n = 8, the most stable Fe₈Au (23 μ_B) with C₁ symmetry is capped one Au atom on the Fe₈ ground-state geometry. The second stable isomer and the third stable isomer have similar geometric configurations with the lowest-energy structure but Au atoms occupy the different capped positions, whose total energies are only 0.046 eV and 0.094 eV above the lowest-energy isomer. The last stable isomer (C₁) with a total magnetic moment of 23 μ_B can be viewed as the Fe atom in the ground state structure of Fe₉ replaced by one Au atom.

For the case of Fe₉Au, the lowest-energy structure with C_s symmetry prefers one capping Au atom on the surface of the ground-state Fe₉ cluster. As shown in Fig. 1, Au atom substituting one Fe atom of a three-capped pentagonal bipyramid structure of Fe₁₀ cluster yields the second and third stable structure of the Fe₉Au cluster with the C_s symmetry, and are 0.038 eV and 0.158 eV in energy less favorable than the most stable structure, respectively. The last stable structure with C_2v symmetry is formed by capping one Au atom on tri-capped triangular prism, which is 0.167 eV higher in energy than the ground state.

In terms of Fe₁₀Au (C_s), the most stable structure is similar to that of the Fe₁₁ cluster which is a tetra-capped pentagonal bipyramid with the Au atom at the vertex position. It has a total magnetic moment 31 μ_B, and is 0.155 eV in energy lower than that of the metastable state. As seen in Fig. 1, the third and the fourth lowest energy structure which can be regarded as Au replacing one Fe atom of the Fe₁₁ cluster have the same geometry but different magnetisms, and are 0.181 eV and 0.339 eV above the lowest-energy structure, respectively.

Just like the Fe₁₂ cluster, the lowest-energy structure of Fe₁₁Au cluster takes an icosahedral growth pattern where Au atom substitutes the Fe site at the apex with a total magnetic moment of 33 μ_B as shown in Fig. 1. Differently, an Au atom capping a peripheral position of the Fe₁₁ cluster produces the second and the fourth lowest-energy structure, where relative energies are 0.068 eV and 0.223 eV, respectively. In comparison, the third lowest-energy structure takes a similar geometry to the most stable structure but the increased magnetic moment (35 μ_B) and is located at 0.114 eV in energy above the ground state.

With regard to Fe₁₂Au cluster, we consider the icosahedral, hexagonal close packed (hcp), rhombic dodecahedral (bcc) and cuboctahedral (fcc) structures as initial geometries. Overall, the most stable configurations we have finally obtained can be looked upon as a substitutional Au impurity in the pure Fe₁₃ cluster, in which Au atom lies at the one vertex site of the icosahedral structure. As shown in Fig. 1, the other low-lying isomers (a, b, c) have notable instablities (0.077, 0.145, and 0.194 eV, respectively).

The overall evolutionary trends for the Fe_nAu series show that for n = 1−2, 4−5, 10−12, the Au doped geometries are similar to those of Fe_n+1 clusters, where the Au atom occupies a substitutional surface site accompanied with a slight distortion in the host cluster. And the way of growing Fe_nAu (n = 6−9) clusters is that the Au atom occupies a peripheral position of Fe_n cluster. This phenomenon can be attributed to the two aspects: on the one hand, Au atom prefers to occupy peripheral location, which can be explained by the cohesive energy (CE) and the surface energy (SE) of the metal atom. To minimize the total energy, the atom with the smaller surface energy and cohesive energy tends to occupy the surface, while the atom with a higher surface energy and cohesive energy favors the interior^[72–74] The surface energy and average cohesive energy of the bulk Au are 1.506 J·m⁻² and 3.81 eV/atom, which are smaller than those of the bulk Fe 2.417 J·m⁻² and 4.28 eV/atom respectively.^[75,76] On the other hand, the atomic size effect also accounts for this. The smaller atoms tend to occupy the more sterically confined core, especially in icosahedral clusters, exhibiting the compression effects finally forming a stable cluster.^[72] The atomic radius of Au is larger than that of Fe atom.^[75] Thus, the Fe atoms prefer to occupy central position, whereas the Au atom prefers to be located at the site of surface. Similar phenomena and explanations also appeared in previous studies.^[61,76–79]

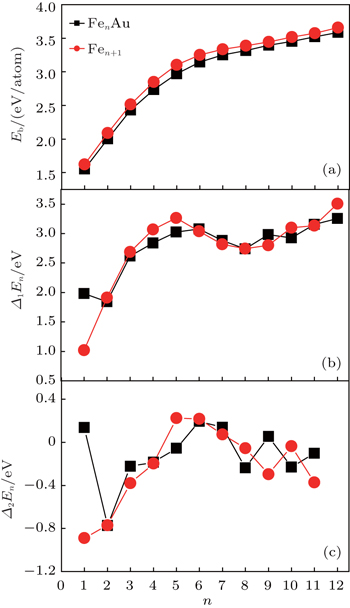
In this subsection, we will investigate the size-dependent physical properties of these clusters. The variation of average binding energy E_b(n) with cluster size is shown in Fig. 2(a). For comparison, we also show the variation of E_b(n) with cluster size for pure iron cluster. The average binding energy E_b(n) is defined as

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Size dependences of averaged atomic binding energies (a), fragmentation energies (b), and second-order difference energies (c) for the lowest energy structures of FenAu and Fen+1 (n = 1−12) clusters.

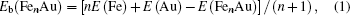
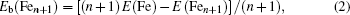
In cluster physics, the fragmentation energies and second-order difference of energies are sensitive indicators of the relative stability. Thus, the size dependence of the fragmentation energies and second-order difference of energies for Fe_nAu (n = 1−12) clusters are further investigated. The fragmentation energy Δ₁E(n) and the second-order difference energy Δ₂E (n) are calculated using the following formulas:

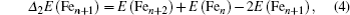
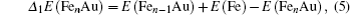
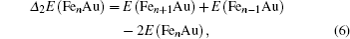
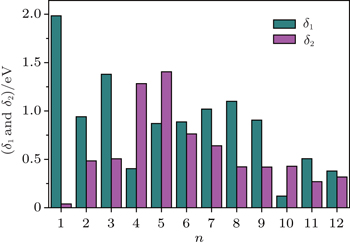
In addition, the HOMO–LUMO gap is a characteristic quantity of electronic structure in clusters and is commonly used to measure the ability for clusters to undergo activated chemical reactions with small molecules. A big energy gap usually corresponds to a high chemical stability. As shown in Fig. 3, FeAu cluster has the narrowest HOMO–LUMO gap, which is only 0.040 eV. However, the gap change trend for Fe_nAu (n = 2−9) clusters which are bigger in energy gap (0.376 eV−0.506 eV) almost keeps a relatively stable value, indicating their high chemical inertness. There are three dramatic drops at n = 10, 11, and 12. The decreases of the gaps (0.120 eV−0.204 eV) suggest that more atoms are involved in the metal-metal bonding.^[80,81] Thus, these clusters could have potential utility in new cluster catalysis nanomaterials as building block with reactive and metallic properties.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. HOMO–LUMO gaps of the most stable structures of FenAu clusters as function of cluster size.

The magnetic stability of these clusters can be verified by calculating the spin gaps as a function of the cluster size. The spin gaps for a magnetic cluster are defined as

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Size dependences of the spin gaps of FenAu (n = 1−12) clusters.

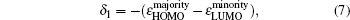
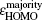
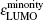
The total magnetic moments of the ground-state Fe_nAu (n = 1−12) clusters are calculated and the results are presented in Fig. 5(a). These results show that the total magnetic moments of the ground-state Fe_nAu (n = 1−12) clusters are 3 μ_B smaller than those of the pure Fe_n+1 with three exceptional jumps of 5 μ_B (Fe₃Au, Fe₁₁Au, and Fe₁₂Au). The valence electron configurations of the free atoms Fe and Au are 3d⁶4s² and 4f¹⁴5d¹⁰6s¹, respectively. For an isolated Fe (Au) atom, the magnetic moment is 4 μ_B (1 μ_B) based on the Hund’s rule. Taking the ferromagnetic alignment into account on the Fe_n+1 and most of Fe_nAu clusters, the unpaired electrons of Fe_n+1 and Fe_nAu clusters will be 4(n+1) and 4n+1, respectively. Therefore, the magnetic moments of the Fe_nAu clusters are supposed to decrease by 3 μ_B. A similar explanation can be found in the studies of Co_n−1Mn and Co_n−1V clusters.^[56] In addition, the average magnetic moments of Fe atom for ground state Fe_n+1 and Fe_nAu clusters are also plotted in Fig. 5(b). It can be seen that the Fe atomic average magnetic moment remains almost unchanged for the case of Au doping, which still keeps about 3 μ_B of magnetism of pure Fe_n+1 clusters. However, the magnetism of Fe_nAu clusters is reduced by 5 μ_B compared with that of the corresponding pure Fe_n+1 clusters, and Fe atomic average magnetic moment of Fe_nAu clusters decreases largely.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Size dependences of the magnetic moments (a) and the average magnetic moments of Fe atom (b) for FenAu and Fen+1 (n = 1−12) clusters.

As shown in Fig. 6, the average bond lengths and average coordination numbers display a similar trend as a function of the cluster size, which is due to their similar geometrical structures. Evidently, in the initial stage for n = 1−4, their average bond lengths increase rapidly, when n goes from 4 to 8, become relatively stable, as n goes from 8 to 12, they increase gradually again. And yet, the average coordination numbers always increase gradually. As is well known, the larger the bond length, the larger the magnetic moment of cluster is, on the contrary, the larger the coordination numbers, the smaller the magnetic moment of cluster is. The consequence of mutual competition of the two factors ultimately determines the most stable structure of each cluster size.^[83,84] Thus, as shown in Fig. 5(b), the average magnetic moment of the Fe_n and Fe_nAu presents an increasing trend in n = 1−4 decreases rapidly in n = 4−8 increases gradually again in n = 8−12. This indicates that the average bond length is dominant in influencing the magnetism of the clusters.

Fig. 6.

	Figure Option ViewDownloadNew Window
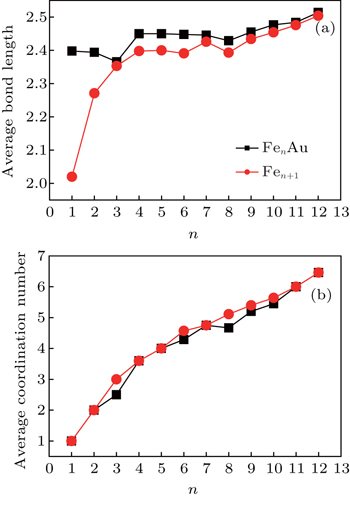	Fig. 6. Variations of average bond length (a) and average coordination number (b) with the cluster size for FenAu and Fen+1 (n = 1−12) clusters.

The reason why the Fe atomic average magnetic moments of n = 3, 11, and 12 alloy clusters obviously decrease compared with that of pure Fe clusters is explained in detail. It can be seen from Fig. 6 that for Fe₁₂Au and Fe₁₃, the average bond lengths remain almost unchanged and average coordination numbers are the same. So the reason most likely is the result of the symmetry. Researches about clusters pointed out that the higher the symmetry, the bigger the magnetic moment is.^[85,86] Generally, the higher symmetry of a cluster forms a narrow d electronic state, which leads to spin splitting more easily, and become a more parallel d electronic spin, consequently generating larger magnetism. Since one Fe atom is substituted by one Au atom at the apex of the icosahedron, the symmetry C_s of Fe₁₂Au is lower than D_5d of Fe₁₃. Thus, the average magnetic moment of Fe atom obviously decreases with respect to pure Fe cluster. This explanation is suitable for Fe₁₁Au cluster. However, Fe₃Au does not have the close-packed tetrahedron geometric structure, but has the complete plane rhombic geometric construction where the dihedral angle is 0 degree. Therefore, Fe₄ with its relative close-packed tetrahedron geometric structure exhibits the stronger spin polarization, while the spin polarization of Fe₃Au is sharply weakened, finally leading to the fact that the average magnetic moment of Fe atom of Fe₃Au cluster is attenuated compared with that of the pure Fe₄ cluster.

For the optimized geometry structure, the total magnetic moments of Fe_nAu clusters, the local moments of Fe and Au atoms, the atomic net charges and the local moments of 3d, 4s, and 4p states for Fe and Au atoms are calculated and summarized in Table 3. The local magnetic moment of per Fe (Au) is the summation of the differences in number between spin-up and spin-down 3d/4s/4p (5d/6s/6p) electrons. The spin magnetic moment of an electron is 1 μ_B.^[83] The atom label is presented in Fig. 7. It can be seen from Table 3 that all of the atoms in the ground states of Fe_nAu alloy clusters are aligned ferromagnetically except for FeAu, Fe₃Au, and Fe₈Au. At the same time, the magnetic moments of the alloy clusters are mainly manipulated by the 3d electrons whereas the s and p electrons contribute only a small amount of net spin. For Fe_nAu clusters, the 4s state of Fe and 5d state of Au all lose some electrons, meanwhile 3d, 4p states of Fe and 6s, 6p states of Au gain extra electrons (see in Table 3). It therefore means that there happens s-pd hybridization in the Fe and Au atoms. As a result, the local magnetic moments of Fe and Au in Fe_nAu clusters are attenuated compared with those of their free atoms. From the analysis of atomic net charge Q, we find that the charge always transfers from Fe to Au atom, which is consistent with the empirical Pauling electro-negativities (χ_p(Fe) = 1.83 eV, χ_p(Au) = 2.54 eV). Thus, this trend of charge transfer leads to the Au atom being nearly non-magnetic. The above results imply that the charge transfer and the strong hybridization between Fe 4s, 3d and Au 6s, 6p, 5d states might be one major reason for inducing magnetism of Fe_nAu cluster.

Table 3.

Table 3.

Table 3. Atom labels and values of atomic net charge Q (e), local magnetic moment μatom (μB) of the atom, Mulliken charge (e), and local magnetic moment of s, p, and d states μL (μB) for the lowest energy structures of FenAu (n = 1−12) clusters. . Clusters Atom label Q μatom Mulliken charge/μL M/μB 3d/5d 4s/6s 4p/6p 1/C∞v Au(1) -0.258 −0.04 9.812/0.062 1.411/−0.117 0.039 / 0.016 3 Fe(2) 0.258 3.04 6.837/3.099 0.838/−0.064 0.067/0.005 2/C2v Au(1) −0.322 0.399 9.678 /0.120 1.496/0.220 0.153 /0.059 7 Fe(2,3) 0.161 3.300 6.757/3.100 0.834/0.148 0.244/0.057 3/C2v Fe(1,3) 0.162 2.973 6.815/2.989 0.698/−0.008 0.319/−0.002 9 Fe(2) −0.001 3.084 6.761/3.035 1.067/0.076 0.170/−0.022 Au(4) −0.323 −0.030 9.716/0.035 1.468/ −0.047 0.144/−0.018 4/Cs Fe(1,5) 0.065 3.769 6.576/3.282 0.821/0.262 0.534/0.232 15 Au(2) −0.220 0.333 9.620/0.158 1.315/0.048 0.291/0.127 Fe(3) 0.044 3.653 6.636/3.193 0.782/0.249 0.533/0.218 Fe(4) 0.045 3.476 6.699/3.171 0.831/0.104 0.422/0.207 5/C2v Fe(1) −0.020 3.191 6.776/3.010 0.735/0.089 0.505/0.099 17 Fe(2,3) 0.057 3.361 6.672/3.158 0.821/0.101 0.446/0.108 Au(4) −0.224 0.295 9.579/0.155 1.265/0.088 0.387/0.053 Fe(5,6) 0.065 3.396 6.693/3.121 0.725/0.161 0.512/0.121 6/Cs Fe(1,2) 0.013 3.208 6.743/3.060 0.826/0.069 0.415/0.086 19 Fe(3) 0.033 2.972 6.805/2.859 0.594/0.049 0.562/0.071 Fe(4) −0.048 3.116 6.777/2.955 0.721/0.085 0.562/0.071 Fe(5,6) 0.127 3.237 6.711/3.074 0.697/0.071 0.546/0.083 Au(7) −0.264 0.022 9.677/0.070 1.341/−0.059 0.253/0.011 7/C1 Fe(1) −0.019 3.069 6.788/2.972 0.825/0.050 0.401/0.055 21 Fe(2) −0.047 2.888 6.826/2.847 0.836/0.027 0.381/0.020 Fe(3) −0.019 3.071 6.787/2.974 0.826/0.049 0.402/0.055 Fe(4) 0.077 3.074 6.784/2.961 0.706/0.046 0.427/0.074 Fe(5) 0.078 3.069 6.785/2.958 0.705/0.045 0.426/0.074 Fe(6) 0.175 2.887 6.787/2.826 0.583/0.010 0.449/0.048 Fe(7) 0.040 2.953 6.777/2.891 0.646/0.033 0.532/0.036 Au(8) −0.283 −0.001 9.684/0.054 1.377/−0.055 0.229/0.001 8/C1 Fe(1) −0.069 2.802 6.863/2.785 0.835/0.013 0.367/0.010 23 Fe(2) −0.036 3.004 6.807/2.948 0.834/0.020 0.391/0.043 Fe(3) 0.146 2.904 6.805/2.843 0.600/0.029 0.445/0.040 Fe(4) 0.033 2.875 6.849/2.824 0.684/0.014 0.429/0.044 Fe(5) 0.034 3.005 6.783/2.927 0.734/0.053 0.446/0.032 Fe(6) 0.183 2.713 6.837/2.686 0.578/0.008 0.398/0.026 Fe (7) 0.061 2.845 6.823/2.816 0.630/0.013 0.482/0.024 Au(8) −0.286 −0.077 9.682/0.046 1.370/−0.117 0.241/−0.006 Fe(9) −0.065 2.928 6.859/2.834 0.802/0.041 0.400/0.060 9/Cs Fe(1,3) 0.031 3.003 6.791/2.957 0.730/0.018 0.443/0.035 27 Au(2) −0.320 0.179 9.655/0.081 1.457/0.061 0.214/0.038 Fe(4,6) −0.014 3.088 6.795/2.961 0.781/0.060 0.434/0.075 Fe(5) 0.014 2.949 6.778/2.886 0.681/0.024 0.523/0.047 Fe(7) 0.225 2.698 6.778/2.685 0.629/−0.022 0.363/0.041 Fe(8) 0.169 2.902 6.800/2.841 0.612/0.011 0.415/0.056 Fe(9,10) −0.061 3.044 6.794/2.946 0.866/0.037 0.415/0.056 10/Cs Au(1) −0.346 0.142 9.652/0.095 1.473/−0.006 0.227/0.054 31 Fe(2,9) −0.076 3.233 6.747/3.052 0.937/0.103 0.389/0.084 Fe(3,10) −0.068 3.191 6.748/2.979 0.845/0.10 0.471/0.113 Fe(4) 0.001 3.072 6.797/2.913 0.703/0.036 0.494/0.131 Fe(5,6) 0.164 2.930 6.810/2.868 0.640/0.006 0.382/0.063 Fe(7) 0.311 2.731 6.803/2.768 0.600/−0.068 0.280/0.037 Fe(8) 0.073 3.026 6.783/2.915 0.647/0.018 0.491/0.100 Fe(11) −0.078 3.322 6.725/3.036 0.920/0.148 0.429/0.144 11/Cs Fe(1,3) 0.009 3.031 6.790/2.897 0.737/0.050 0.457/0.092 33 Fe(2,4) −0.083 3.142 6.757/2.998 0.854/0.065 0.469/0.087 Fe(5) −0.007 3.021 6.820/2.917 0.754/0.040 0.428/0.071 Fe(6) −0.040 3.126 6.759/2.914 0.773/0.085 0.504/0.135 Fe(7,9) −0.053 3.093 6.763/2.967 0.836/0.040 0.450/0.092 Fe(8,10) −0.021 3.016 6.790/2.882 0.730/0.033 0.495/0.110 Fe(11) 0.681 2.107 6.981/2.263 0.579/−0.098 −0.249/−0.052 Au(12) −0.338 0.182 9.596/0.076 1.326/0.073 0.425/0.032 12/Cs Fe(1,11) −0.055 3.221 6.745/2.994 0.771/0.069 0.535/0.166 39 Fe(2) −0.067 3.342 6.703/3.037 0.817/0.123 0.542/0.190 Fe(3,7) −0.053 3.395 6.681/3.090 0.829/0.142 0.540/0.171 Fe(4,6) −0.032 3.393 6.692/3.085 0.813/0.157 0.523/0.159 Fe(5) −0.013 3.466 6.660/3.116 0.801/0.161 0.549/0.197 Fe(8) −0.041 3.464 6.651/3.113 0.817/0.148 0.570/0.211 Fe(9,12) −0.026 3.190 6.754/2.981 0.759/0.066 0.508/0.150 Au(10) −0.331 0.237 9.553/0.096 1.271/0.073 0.519/0.068 Fe(13) 0.783 2.093 7.073/2.388 0.640/−0.122 −0.509/−0.168

Table 3. Atom labels and values of atomic net charge Q (e), local magnetic moment μatom (μB) of the atom, Mulliken charge (e), and local magnetic moment of s, p, and d states μL (μB) for the lowest energy structures of FenAu (n = 1−12) clusters. .

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. Atom labels of the ground state of FenAu (n = 1−12) clusters.

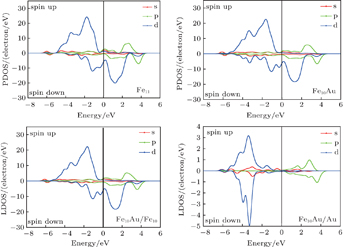
To gain an insight into the magnetism of the Fe_nAu cluster, we also explore the spin densities of the alloy clusters. In Fig. 8, for proper comparison, we plot the differences between the charge density for spin-up electrons and that of spin-down electrons for Fe_n+1 (n = 1−12) clusters. As seen from Fig. 8, the contributions to magnetism of the cluster mainly originate from Fe atoms in Fe_nAu and the Au atom has no influence on magnetism. Meanwhile, the spin density volume of the Fe atom has almost no change after substituting an Fe atom with an Au atom, which means that the local magnetic moment of Fe in Fe_nAu is nearly equal to those in Fe_n+1 (n = 1−12) clusters. Meanwhile, the doping-Au atom has no spin density, which is consistent with the fact that the Au atom is almost nonmagnetic. In addition, to further ascertain the reason for reducing the magnetic moment, we perform detailed analyses of spin polarization (P) of Fe atomic d orbital for Fe_n+1 and Fe_nAu alloy clusters in the Supporting Information Table S1. The results show that the average spin polarizations of d orbital of Fe atom for Fe_n+1 and Fe_nAu alloy clusters are almost identical. Therefore, doping with the Au atom results in reducing the total magnetic moment of Fe_nAu clusters, while it has no effect on the local magnetic moment of Fe atom.

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. spin densities of FenAu and Fen+1 (n = 1−12) clusters. The density isosurfaces are drawn at 0.5 a.u.

In order to explore the magnetic origin further, In Fig. 9, we present the s-, p-, and d-projected partial densities of states (PDOSs) and local densities of states (LDOSs) of Fe₁₁ and Fe₁₀Au clusters as representatives. (See the Supporting Information about the PDOS and LDOS contributions of Fe₁₃ and Fe₁₂Au clusters). It is clearly seen that the magnetic moments of these clusters mainly come from d states, while the s and p states only contribute a small amount of net spin, which is in good agreement with the above Mulliken population analyses of the on-site atomic charges and the atomic spin density. For Fe₁₁, we find that the up- and down-spin channels of the d PDOS are seriously asymmetric, which has a magnetic moment of 34 μ_B. Substituting Fe atom by Au reduces the up-spin channel, and a small peak of the down-spin d PDOS is broadened around −4.2 eV below the Fermi level, which consequently enhances significantly the depletion of down-spin d states, finally leading to the total magnetic moment reducing 3 μ_B. In addition, the up-spin channels of Fe₁₀Au/Fe₁₀ is evidently larger than that of down-spin, leading to the characteristic ferromagnetic exchange splitting with the local magnetic moment of 30.858 μ_B. For Fe₁₀Au/Au, the distributions of the up- and down-spin d electrons are nearly equal, resulting in lower spin polarization. So the local magnetic moment of Au in Fe₁₀Au clusters is only 0.142 μ_B. This further confirms that the Fe atomic magnetism is the main contribution to the Fe₁₀Au cluster magnetic moment.

Fig. 9.

	Figure Option ViewDownloadNew Window
	Fig. 9. PDOSs and LDOSs of Fe10Au and Fe11 clusters.