Cite this Article
Wang Qing-Qing, Li Peng, Gao Tao, Wang Hong-Yan, Ao Bing-Yun. Density function theoretical study on the complex involved in Th atom-activated C–C bond in C2H6. Chinese Physics B, 2016, 25(6): 063102  
Permissions
Density function theoretical study on the complex involved in Th atom-activated C–C bond in C2H6
Wang Qing-Qing1, Li Peng2, Gao Tao1, †, , Wang Hong-Yan3, Ao Bing-Yun4
Institute of Atomic and Molecular Physics, Sichuan University, Chengdu 610065, China
College of Physics and Electronic Engineering, Shanxi University, Taiyuan 030006, China
School of Physical Science and Technology, Southwest Jiaotong University, Chengdu 610031, China
Science and Technology on Surface Physics and Chemistry Laboratory, P. O. Box 9071-35, Jiangyou 621907, China

 

† Corresponding author. E-mail: gaotao@scu.edu.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 21371160, 21401173, and 11364023).

Abstract
Abstract

Density functional theory (DFT) calculations are performed to investigate the reactivity of Th atom toward ethane C–C bond activation. A comprehensive description of the reaction mechanisms leading to two different reaction products is presented. We report a complete exploration of the potential energy surfaces by taking into consideration different spin states. In addition, the intermediate and transition states along the reaction paths are characterized. Total, partial, and overlap population density of state diagrams and analyses are also presented. Furthermore, the natures of the chemical bonding of intermediate and transition states are studied by using topological method combined with electron localization function (ELF) and Mayer bond order. Infrared spectrum (IR) is obtained and further discussed based on the optimized geometries.

PACS: 31.10.+z;33.20.Ea;31.15.ae;31.15.E−
Keyword:reaction mechanism;Mayer bond order;electron localization function;density of states
1. Introduction

Thorium has vast potential for the future development of application in nuclear power, which can supplement the shortage of the uranium resources effectively. In the application of the nuclear material, one of the challenges is the corrosive effect with environmental atmosphere, e.g. with water, oxygen, etc. Moreover, it is quite difficult to study the corrosive effect experimentally due to the virulence and radioactivity of Th atom. Therefore, it requires a reliable and accurate theoretical model to study the physical property of compounds involved in the process of corrosion.

Over the past few decades, reactions of actinide cations with the ordinary small molecules in the air have drawn considerable attention. The majority of these studies focused on analyzing the quite different electronic structures, the reactivity, and bonding of the actinide ions. Experimentally, Santo and Santos detected the following reaction products for the reaction of Th2+ with CH4:[1]

and for the reaction of Th2+ with C2H6:

They also studied the gas-phase ion chemistry of the original actinides, including Th, Pa, U, Np, Pu, Am, and Cm,[2–7] using Fourier transform ion cyclotron resonance mass spectrometry (FTICR-MS).[8] Among the complex minimum energy reaction paths, there are two different reaction paths: the activations of C−C and C−H. The reaction products of Th2+ with C2H6 were ascertained in their research.

In addition, Li et al. studied many systems about the reactions of actinium (An = Th, U, Np, Pu, and relevant cation) with inorganic molecules including H2O and NH3[9–15] theoretically. They also obtained the similar mechanisms in all the studied reactions.

However, as far as we know, there are neither experimental data on the direct reaction of Th atom with C2H6 molecule nor theoretical studies on the geometries nor the topological analysis of the reaction products. The main objective of the present work is to give an insight into the reaction of Th atom with C2H6. The paper reports the molecular structures and topological analyses of all the intermediates involved in the activation process of C−C. The bonding evolution during the reaction pathways is investigated by Mayer bond order and electron localization function (ELF). We analyze the roles of 5f orbitals by means of total density of states (TDOS), partial density of states (PDOS) and overlap potential density of states (OPDOS).[16] In addition, the IR spectrum of the intermediate is investigated based on the optimized geometry.

2. Computational details

All theoretical calculations were carried out with the Gaussian09 package[17] using density functional theory (DFT). The B3LYP[18–20] hybrid functional (Becke’s three-parameter hybrid functional with the Lee, Yang and Parr correlation functional) was adopted for all intermediate and transition states along the reaction pathways. To assess the veracity of the current calculation scheme, we also adopted other methods including pure GGA PW91,[21,22] the Meta-GGA TPSS,[23] the PBE0,[24] and PBE.[25] In all calculations the Stuttgart small-core relativistic effective core potential (RECP)[26] for Th atom was applied. The Stuttgart small-core RECP treated the 60 electrons in the inner core shells of thorium with pseudopotentials, and the valence shells by using a segmented contraction scheme of (5s5p5d5f6s6p6d7s). The split-valence shell Gaussian basis sets, 6-311++G(d,p),[27,28] were employed to handle C and H atoms in full optimization and frequency calculations (we refer to these results as B3LYP/SDD hereafter). The computational scheme was carried out successfully in a previous mechanism study of gas-phase actinide chemistry. All of the targeted structures were fully optimized in the gas phase, and the nature of special points was characterized by vibrational analysis to be either local minima or saddle points on the potential energy surface. We ensure that each transition state has only one imaginary frequency, and that this frequency is related to reactants and products by the intrinsic reaction coordinate (IRC) calculations. Because of the possibility of spin crossovers involved in the reaction pathways, we considered all possible spin states of Th (singlet, triplet, and quintet). We generally referred to this feature as two-state reactivity. We checked the 〈S2〉 values to evaluate whether spin contamination can influence the quality of the results. In all cases we found that the calculated values differ from S(S + 1) within less than 5%. IR spectra of intermediates were investigated based on the optimized geometries.

To obtain a full understanding of the nature of the bonding evolution along the reaction pathway, Mayer bond order[29] and ELF were performed with the Multiwfn[30] package. We replaced 6-311++G(d,p) with 6-311G(d,p) during the calculation of Mayer bond order because of the inaccuracy when there are diffusion functions. To understand the role of 5f electrons in the chemical bonds of thorium complexes, TDOS, PDOS, and OPDOS were calculated.

3. Results and discussion
3.1. Reaction mechanisms

The reaction under study is involved in the C−C activation of Th + C2H6. The potential energy profile and the geometric structure corresponding to all of the intermediates and transition states involved in this system are shown in Fig. 1. The vibrational frequencies for the transition states are also presented. Summarized in Table 1 are the activation barriers associated with all the transition states. The results indicate that the two methods give consistent results.

Fig. 1. Geometric structures and potential energy profiles for the reaction of Th + C2H6, computed at the B3LYP/SDD and PW91/SDD (in parentheses) levels of theory.
Table 1.

Activation barriers (kcal/mol) of the transition states.

.

From Fig. 1 we can see that the reaction path evolves along the triplet spin surface during the formation of the Th−C2H6 initial complex. As can be seen, there is an intersystem crossing between the quintet and triplet PES after the forming of TS1. Then, the reaction proceeds along the singlet spin surface. Immediately after that, the IM1 intermediate can proceed directly to the IM2 intermediate via a second transition state, TS2, which is characterized by imaginary frequencies (502.44 cm−1 at B3LYP/SDD and 416.99 cm−1 at PW91/SDD) that involve the stretching of the C−C bond. It is obvious that the intermediate IM2 has a global minimum of the potential energy profile and i.e., −62.06 kcal/mol below the ground state reactants. After that, the reaction proceeds toward the formation of the demethylation products, Th + C2H6 → FC → TS1 → IM1 → TS2 → IM2 → ThCH3 + CH3, as a result of a simple cleavage of the Th−C bond in the intermediate IM2, or the formation of IM3, Th + C2H6 → FC → TS1 → IM1 → TS2 → IM2 → TS3 → IM3 → ThCH2 + CH4, after rising to the third transition state (TS3) energy, which occurs below the energy of the reactants, a hydrogen atom is shifted from Th atom to the C atom, leading to the IM3. The intermediate IM3 can directly dissociate into the ThCH2 + CH4 channel.

For a system, when there are no experimentally determined structural parameters and energy values, it is important to study the system using different functionals to see whether they give consistent results. Therefore, in addition to the B3LYP/SDD and PW91/SDD levels of theory used in this study, we also investigate the potential energy surfaces at several other levels of theory, including the PBE0/SDD, PBE/SDD, BMK/SDD and TPSS/SDD. Table 2 presents the relative energies of special stationary points on the PESs. The ranges of these methods should provide a broad survey of the structures and energetics associated with the dissociation reaction of ThC2H6. As can be seen, for transition state TS2, PBE0/SDD and PBE/SDD overestimate the energy, while BMK/SDD gives an underestimated energy. The TPSS/SDD method gives an overestimated energy of transition state TS1.

Table 2.

Relative energies (kcal/mol) of the stationary points on the PathB potential energy surface.

.
3.2. Bonding evolution analysis
3.2.1. ELF analyses

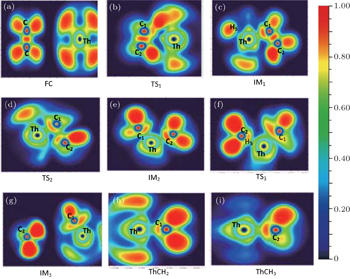
As previously mentioned, the bonding properties of all the species involved in the studied reaction pathways are investigated by using ELF function. The details of the analyses are as follows. The ELF projection figures of the compounds involved in the C−C activation are presented in Fig. 2. As shown in Fig. 2, the absence of a disynaptic valence basin between Th and the carbon and hydrogen atoms of C2H6 indicates that there is no covalent bond, which confirms that the interaction could be considered as an electrostatic interaction. The ELF of TS1 structure shows that the first C1−H5 bond breaking takes place at this stage. This fact is evidenced by the weakening of the V(C1, H5) basin (see Fig. 2) and it is replaced by a trisynaptic basin. As for IM1(ThC2H6), there appears the strengthening of the trisynaptic V(C1, Th, H5) basin, giving place to the absence of a disynaptic V(C1, H5) basin. This proves the breakage of the C1−H5 bond at this stage and the formation of the Th−H5 covalent bond. The ELF analysis of the TS2 shows the weakening of V(C, C) disynaptic valence basins, which indicates that the C−C is broken at this step. The ELF analysis indicates that the C−C bond is completely broken at the step of IM2 formation, as evidenced by the disappearance of the V(C1, C2) and the formation of the trisynaptic V(C1, Th, C2) basin. The H5 migrates from Th to C2 atom at the stage of the TS3. The ELF analysis shows that the H5−Th bond is not yet completely broken as evidenced by the existence of the trisynaptic V(C2, Th, H5) basin. In the case of IM3, the ELF analysis shows the lack of V(C1, Th, C2) trisynaptic valence basins, giving place to the formation of a disynaptic V(C2, H5) basin. This is an indication of the broken of C2−Th bond at this stage and the formation of a C2−H5 bond. By this time, the IM3 intermediate can directly dissociate into the ThCH2 + CH4.

Fig. 2. ELF projection map (η = 0.70) of stationary points on the C−C activation of TH + C2H6 reaction pathway at B3LYP/SDD level.
3.2.2. Mayer bond order

In order to gain an in-depth understanding of the reaction mechanisms, we investigate the evolution of the bonds along the pathways using Mayer bond order. Figure 3 shows the energy and Mayer bond order along with the intrinsic reaction coordinates of Th + C2H6 reaction, which are calculated at the B3LYP/SDD and PW91/SDD levels. Mayer bond order analyses for all of the minima and transition states involved in the reaction of Th + C2H6 at the B3LYP/SDD level of theory are listed in Table 3. As discussed above, due to the B3LYP and PW91 methods performed well in the geometry optimization and frequency calculations, we chose them to complement each other to provide a more credible bond analysis.

Fig. 3. IRC energies and Mayer bond orders along the reaction coordinates, calculated at the B3LYP/SDD (above) and PW91/SDD (below) levels. Solid curves are for the energy, and dashed lines are for the Mayer bond order (the vertical axes represent the total energy/Hartree (right) and Mayer bond order (left), respectively).

The solid lines represent total energy and the dashed lines represent different bonds in this pathway, respectively. From Figs. 3(a) and 3(b) we can see that the Th9−H5 bond order gradually increases in the process of FC → TS1 → IM1, while the C1−H5 bond order gradually decreases to zero. It is shown that the C1−H5 bond breaks at this stage, which is consistent with the descriptions of the reaction mechanisms and the ELF analyses. As for the IM1 → TS2 → IM2, the increasing of Th9−C2 bond order indicates its formation. Meanwhile, the C1−C2 bond order gradually decreases to zero in the forming process of IM2, implying the fracture of C1−C2 bond as indicated by the ELF analyses. It is quite clear that the Th9−C2 and Th9−H5 bonds rupture and the C2−H5 forms in the process of IM2 → TS3 → IM3.

As can be seen from Fig. 3, in the process of IM2 → TS3 → IM3, the Th9−H5 bond order curve has a small valley in the place closer to the transition state. The reason could be that the TS3 is quite different from other species, which has a basin where more electrons of the system accumulate than other basins. In addition, the positions of the transition states are near the crossing region of these two sets of bond orders (the forming bond order and the breaking bond order).

Table 3.

Mayer bond order analysis for all of the minima and transition states involved in the reaction of Th + C2H6 at the B3LYP/SDD level of theory.

.
3.2.3. Density of states

As is well known, the diffuse character of 5f orbitals, which are relatively spread out and close to the outermost 7s atomic valence orbital, may increase the size of the activation barrier.[31,32] To obtain more information about the roles that the 5f electrons and 5f orbitals play in thorium species, the TDOS, PDOS, and OPDOS are calculated. The TDOS, PDOS, and OPDOS drawings of all special points along the pathway are shown in Fig. 4. The orbitals are canonical molecular orbitals (MOs); fragment 1 is defined as f-shells of thorium (corresponding to 5f atomic orbitals), fragment 2 is defined as hydrogen and carbon atoms, both original and broadened TDOS/ PDOS/ OPDOS are shown in the graph below. The height is only meaningful for lines (original data) but not for curves. The vertical dashed line indicates the position of highest occupied molecular orbital (HOMO) level. Since the dashed-dotted curve being greater or less than zero respectively represents that the corresponding MOs are favorable or unfavorable for forming a chemical bond between the thorium atom 5f-orbitals and carbon and hydrogen atoms, it is shown that the high-energy state orbitals (> 0 a.u., the unit a.u. is the atomic unit) are not conducive for bonding (namely anti-bonding character). These conclusions can be confirmed further by observing isosurfaces of corresponding MOs. Figure 4 shows that the PDOS−C, H curve is high and approaches to the TDOS line in a region from −0.7 a.u. to −0.2 a.u. As a result, we can conclude that carbon and hydrogen atoms’ orbitals contribute significantly to the corresponding molecular orbitals. At the position of the HOMO level, the 5f orbitals of the thorium atom approach the TDOS line, which means that most of the contributions to the HOMO come from the 5f orbitals of thorium atom.

Fig. 4. The TDOS, PDOS, and OPDOS curves for all special points in the reaction of TH + C2H6 computed at the B3LYP/SDD levels of theory.
3.3. IR spectrum

IR spectrum is an effective tool to identify the complexes based on the characteristic functional groups. The simulated infrared spectrum results of critical compounds (reactants, intermediates, and products) are shown in Fig. 5.

Fig. 5. IR spectra of critical compounds (the unit of vertical axis is L/mol·cm−1.

The calculated IR results show that FC has one characteristic peak (2890.12 cm−1). The peak is assigned to the closer vibration modes between the Th atom and C2H6 molecule. IM1 has two characteristic peaks (1404.92 cm−1 and 472.60 cm−1). The strongest peak is assigned to the asymmetrical stretching modes of Th atom and H5 atom, while the 472.60 cm−1 is from the stretching of Th atom and C atom. As for the intermediate IM2, the peak at 1403.87 cm−1 is from the stretching mode of Th−H5 bond. The weaker one at 68.33 cm−1 comes from asymmetrical stretching modes of Th−C1 bond and Th−C2 bond. The strongest peak corresponds to 765.85 cm−1 and is assigned to asymmetrical stretching of C1−C2 for the IM3. The second strongest IR absorption for the IM3 corresponds to the Th−C2 stretching mode calculated at 582.12 cm−1, and its IR intensity is 1.51 km/mole. In addition, the characteristic peaks at 1482.23 cm−1 (FC), 2788.45 cm−1 (IM3), and 1167 cm−1 (IM2) are mainly dominated by the stretching of C−H bond and out-of-plane deforming of methyl.

4. Conclusions

In this work, the theoretical calculations are performed to investigate the detailed mechanism of the C−C activation of C2H6 by Th atom. The present results contribute to a better understanding of the title reactions. The main conclusions can be summarized as follows.

Reference
1Di Santo EmanuelaSantos Marta 2011 J. Am. Chem. Soc. 133 1955
2Santos MMarc-alo JPires de Matos AGibson J KHaire R G 2002 J. Phys. Chem. 106 7190
3Santos MMarc-alo JLeal J PPires de Matos AGibson J KHaire R G 2003 Int. J. Mass Spectrom. 228 457
4Gibson J KHaire R GSantos MMarc-alo JPires deMatos A 2005 J. Phys. Chem. 109 2768
5Gibson J KHaire R GMarc-alo JSantos MPires deMato A Leal 2005 J. P. J. Nucl. Mater. 344 24
6Santos MPires de Matos AMarc-alo JGibson J KHaire R GTyagi RPitzer R M 2006 J. Phys. Chem. 110 5751
7Gibson J KHaire R GSantos MPires de Matos AMarc-alo J 2008 J. Phys. Chem. 112 11373
8Marshall A GHendrickson C LJackson G S 1998 Mass Spectrom. Rev. 17 1
9Li PNiu W XGao TWang H Y 2014 J. Mol. Model. 20 2466
10Niu W XZhang HLi PGao T 2015 Int. J. Quantum Chem. 115 6
11Li PNiu W XGao TWang H Y 2014 Chem. Phys. Chem. 15 3078
12Li PNiu W XGao TWang H Y 2014 Int. J. Quantum Chem. 114 760
13Li PNiu W XGao T 2015 J. Radio. Nucl. Chem. 304 489
14Li PNiu W XGao T 2014 RSC Adv. 4 29806
15Li PNiu W XTian X FGao TWang H Y 2013 J. Phys. Chem. 117 3761
16Maecki J G 2010 Polyhedron 29 1973
17Frisch M JTrucks G WSchlegel H BScuseria G ERobb M ACheeseman A JScalmani GBarone VMennucci BPetersson G ANakatsuji HCaricato MLi XHratchian H PIzmaylov A PBloino JZheng GSonnenberg J LHada MEhara MToyota KFukuda RHasegawa JIshida MNakajima THonda YKitao ONakai HVreven TMontgomery J AJrPeralta J EOgliaro FBearpark MHeyd J JBrothers EKudin K NStaroverov V NKobayashi RNormand JRaghavachari KRendell ABurant J CIyengar S STomasi JCossi MRega NMillam J MKlene MKnox J ECross J BBakken VAdamo CJaramillo JGomperts RStratmann R EYazyev OAustin A JCammi RPomelli COchterski J WMartin R LMorokuma KZakrzewski V GVoth G ASalvador PDannenberg J JDapprich SDaniels A DFarkas CForesman J BOrtiz J VCioslowski JFox D JGaussian 09 (Revision A.02) Gaussian, Inc., Wallingford CT, 2009
18Becke A D 1993 J. Chem. Phys. 98 1372
19Becke A D 1993 J. Chem. Phys. 98 5648
20Lee CYang WParr R G 1988 Matter Mater. Phys. 37 785
21Perdew J PChevary J AVosko S HJackson K APederson M RSingh D JFiolhais C 1992 Phys. Rev. B: Condens. Matter Mater. Phys. 46 6671
22Perdew J PBurke KWang Y 1996 Phys. Rev. B: Condens. Matter Mater. Phys. 54 16533
23Tao JPerdew J PStaroverov V NScuseria G E 2003 Phys. Rev. Lett. 91 146401
24Adamo CBarone V 1999 J. Chem. Phys. 110 6158
25Perdew J PBurke KErnzerhof M 1996 Phys. Rev. Lett. 77 3865
26Kchle WDolg MStoll HPreuss H 1994 J. Chem. Phys. 100 7535
27Krishnan RBinkley J SSeeger RPople J A 1980 J. Chem. Phys. 72 650
28Blaudeau J PMcGrath M PCurtiss L ARadom L 1997 J. Chem. Phys. 107 5016
29Mayer I 1983 Chem. Phys. Lett. 97 270
30Lu TChen F 2012 J. Comput. Chem. 33 580
31Gibson J K 2002 J. Mass Spectrosc. 214 1
32GibsonJ KMarcalo CoordJ 2006 Chem. Rev. 250 776