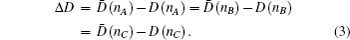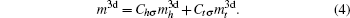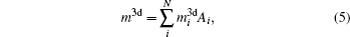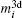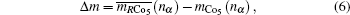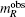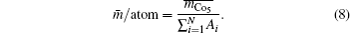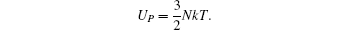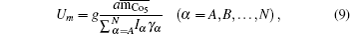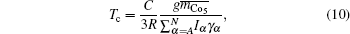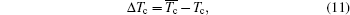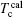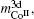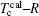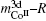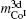Correlation between valence electronic structure and magnetic properties in RCo5 (R = rare earth) intermetallic compound

Cite this Article

Xue Zhi-Qin, Guo Yong-Quan. Correlation between valence electronic structure and magnetic properties in RCo₅ (R = rare earth) intermetallic compound. Chinese Physics B, 2016, 25(6): 063101 Copy to clipboard

Permissions

Correlation between valence electronic structure and magnetic properties in RCo₅ (R = rare earth) intermetallic compound

Xue Zhi-Qin, Guo Yong-Quan^†,

North China Electric Power University, School of Energy Power and Mechanical Engineering, Beijing 102206, China

† Corresponding author. E-mail: yqguo@ncepu.edu.cn

Project supported by the National Natural Science Foundation of China (Grant No. 11274110).

Abstract

The magnetisms of RCo₅ (R = rare earth) intermetallics are systematically studied with the empirical electron theory of solids and molecules (EET). The theoretical moments and Curie temperatures agree well with experimental ones. The calculated results show strong correlations between the valence electronic structure and the magnetic properties in RCo₅ intermetallic compounds. The moments of RCo₅ intermetallics originate mainly from the 3d electrons of Co atoms and 4f electrons of rare earth, and the s electrons also affect the magnetic moments by the hybridization of d and s electrons. It is found that moment of Co atom at 2c site is higher than that at 3g site due to the fact that the bonding effect between R and Co is associated with an electron transformation from 3d electrons into covalence electrons. In the heavy rare-earth-based RCo₅ intermetallics, the contribution to magnetic moment originates from the 3d and 4f electrons. The covalence electrons and lattice electrons also affect the Curie temperature, which is proportional to the average moment along the various bonds.

PACS: 31.10.+z;31.30.–i

Keyword:EET theory;electronic structure;Curie temperature;RCo₅ intermetallics

Show Figures

1. Introduction

Owing to the large magnetocrystalline anisotropies, high Curie temperatures and high saturation moments at room temperature, RCo₅ (R = rare earth) intermetallic compounds have received considerable scientific and technological attention in the past decades,^[1,2] and the studies have covered the experiment, theory and technology for developing the advanced rare earth permanent magnetic materials.^[3–5] The study on magnetic properties of RCo₅ intermetallic compounds is derived from the magnetization measurements on single crystals.^[6] Rao and Greedan have established the relationships between the basic parameters in crystal-field theory and the magnetocrystalline anisotropy in most RCo₅ intermetallic compounds.^[7] The single-ion anisotropy has been found to have a fundamental influence on the behavior of the magnetic system and the related mechanism has been studied.^[8,9] In many cases, the single-ion anisotropy model contains many calculating parameters especially in the Heisenberg model proposed based on the exchange coupling interaction. As for the first principle theory, the magnetic properties of RCo₅ compounds are usually discussed within a two-sublattice model consisting of R and Co sublattices.^[10,11] The computational methods based on the density functional theory (DFT) provide an important insight into the electronic structure and the related physical properties for the various materials. The basic DFT approximation (local spin density approximation-LSDA) is usually restricted to the so-called open core treatment of the 4f electrons.^[12,13] However, LSDA could not predict the energetics of the various magnetic orders due to the absence of the energy gap between the filled and the empty states and underestimations of the orbital magnetic moments.^[14,15] The theoretical work on the anisotropy and Curie temperature of R–(Fe,Co) magnetic alloys were carried out in the molecular-field approximation by studying the exchange coupling interactions between the 3d electrons of Fe or Co and 4f electrons of rare earth.^[16] However, there are too many theoretical parameters in the complicated calculation. Also, the samples should be of the single-crystal.^[17]

As for the first principle theory, it could not initially be used to study the magnetism of rare-earth-based intermetallic compounds. In recent years, a framework of the LSDA + U approach has been developed to calculate the magnetic properties of rare earth alloys and compounds based on the mean-field theory.^[18] However, the calculation is restricted by the structural cell model and the capacity of the computer. In the present paper, we use the empirical electron theory of solids and molecules (EET), which is based on Pauling’s electron theory of metals.^[19] Owing to its lesser computing parameters than the molecular-field and the first principle theories, the model is simpler than the theories of crystal-field and first-principle without considering any integral or differential calculation. The EET can be used to investigate the correlations between the valence electronic structures and multiple physical properties of solid state materials. The approximations, which are based on the electronic structures, can work in studying the essential mechanisms of physical phenomena as reported. On one hand, the electronic structure analyses could reveal many natures of physical phenomena such as: orbital hybridization, band gap between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO), vertical ionization potentials, and electron affinities, which are important for studying the correlations between the electronic structures and physical properties in molecules and solids.^[20–22] The multiple properties such as cohesive energy, melting point, transition temperature, magnetic moment, Curie temperature, superconductor temperature, etc. have been calculated based on the electron states in the electronic structure.^[23–26] In this study, the magnetic moments and Curie temperatures of RCo₅ (R = Y, La, Ce, Pr, Nd, Sm, Gd, Tb, Dy, Er) intermetallics are systematically studied with EET and the relations between the electronic structures and magnetic characteristics of these compounds are discussed as well.

2. Empirical electron theory (EET)

EET is a semi-empirical theory based on the Pauling valence-bonding theory and Hume–Rothery electron concentration rule. As a supplement, the equivalence valence electron hypothesis is introduced for the application of the electron theory to the crystal structures. The theory consists of three general hypotheses and one method of calculating bond distances. Hypothesis 1: the atoms in a solid and a molecule are in general hybridization of the two states, which can be called the h (head) and t (tail) states. Both states have one or two kinds of valence electrons; that is, covalent and newly introduced lattice electrons. Hypothesis 2: the hybridization of the two states is discontinuous, allowing only certain relative compositions to be calculated by a k-equation. Hypothesis 3: the covalent bond length between atom u and v with the number of covalent electron pairs denoted by n_α is related by

where R_u(1) and R_v(1) denote the radii of single-bond for u and v atoms, respectively. The parameter β can reflect how much the electron clouds of the u and v atoms overlap each other, and β values are 0.6 for metals and alloys and 0.71 for the other nonmetal compounds, respectively. Here a modification of Pauling’s theory is made for (n − 1) value according to the maximum of n_α (α = A,B,C,…,N), and the (n − 1) values are listed below.

The bond length difference (BLD) analytical method: the method is trying to find the derivations (ΔD) between the theoretical D(n_α) and experimental bond lengths D(n_α) until ΔD ≤ 0.05 Å. For calculating the theoretical bond lengths D̄(n_α)(α = A,B,C,…N), the n_α (α = A,B,C,…,N) values should be first calculated based on (α = B,C,…,N) experimental bond length difference [D(n_A) − D(n_α)] equations as reported in Ref. [17]. The theoretical bond lengths D(n_α) could be calculated by substituting the n_α (α = A,B,C,…,N) values into Eq. (1).

From the derivation, it is seen that

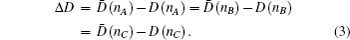
Hence the difference ΔD is a criterion for all the D̄(n_α)’s, that is, the theoretical explanation for all the D̄(n_α)’s of a crystalline or molecular structure. If it is smaller than 0.05 Å, it proves that the valence bond electron distribution is correct in the first order approximation. However, the only criterion limitation of ΔD is not enough to determine the electronic structure. Thus, the extra physical property criterions, such as melting point, cohesive energy, magnetic moments are necessary. Here the moment and Curie temperature criterions are discussed.

3. Calculations of magnetic moment and Curie temperature

3.1. Magnetic moments^[23]

According to the criterion of ΔD ≤ 0.05 in the BLD method, the hybridization states of the electrons in solid and molecules could be determined, and the relative values of C_hσ and C_tσ are determined.

Then there is given the equation for calculating the magnetic moments:

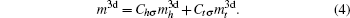
For a molecule, we then have

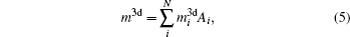
where A_i and

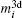
denote the atom number of the i-th atom and its 3d magnetic electron number. The Δm is also considered as a criterion for all the m^3d for the Co atoms at 2c and 3g sites, and expressed as

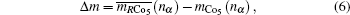
with

where the m_Co5(n_α) and m_Co5 (n_α) are corresponding to the theoretical and observed magnetic moments.

The magnetic moments of rare earth 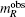are the theoretical moments in ordered status gμ_BJ (J is angular momentum). The moment contributed by 4f electron of rare earth depends on 4f electron spin alignment at R sublattice, and its values are positive for light rare-earth- (LRE) based RCo₅ compounds and negative for the heavy rare-earth- (HRE) based RCo₅ compounds, respectively. Therefore, the average magnetic moment per atom is

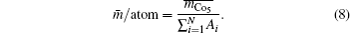
About all, the criterion Δm gives another limitation for estimating the calculations.

3.2. Curie temperature

The model for calculating Curie temperature is based on the assumption of molten ferromagnetic order structure by the heat vibrations induced by the phonon energy with increasing temperature. When the temperature reaches a certain value of T_c, the phonon energy equals the magnetic energy. If T > T_c, the magnetic order is molten and the ferromagnetic characteristics disappear. This transition temperature is regarded as the Curie temperature. The energy of N phonons is

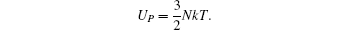
The average magnetic energy per bond is

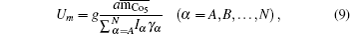
where U_p and U_m denote the phonon and magnetic energy, respectively. When U_p = U_m, and g = 2.2 for Co, then we have

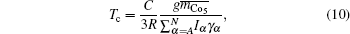
where R = 8.31 J/mol, and C = 1.542 × 10⁴.

Then here is given the criterion, ΔT_c.

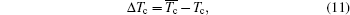
where the T_c and T_c denote the calculated and observed Curie temperature respectively.

In summary, the theoretical D (n_α)’s should fit to all the limitations of ΔD, Δm, and ΔT_c well, and then the relations between the magnetic characteristics and electronic structures in the exact hybridization can be revealed. The calculated results are listed in Tables 1–3.

Table 1.

Lattice parameters of RCo₅ and valence bond lengths.

Table 2.

Calculation results of magnetic properties. In this table, n_α (max) denotes the maximum number in the covalent electron pairs n_α (α = A,B, … N), and the symbol “–” refers to the negative moment originating from the heavy rare earths since their moment arrangements are anti parallel to the direction of 3d moment of Co.

Table 3.

Analyses of valence electronic structures of RCo₅. In this table, n_c, n_l, m^3d, and n_T denote the numbers of the covalent electrons, the lattice electrons, the magnetic electrons, and the total number of the electrons, respectively; σ is the number of quantum states. The rare earth element has a piece of the hybridization table, which possesses 10 kinds of quantum states. Element Co has 8 pieces of the hybridization table (A₁, A₂, B, C₁, C₂, D, E₁, E₂), and each of them records 18 kinds of quantum states.

4. Calculated results and discussion

4.1. Crystal structures of RCo₅ compounds

RCo₅ compounds crystallize into the hexagonal CaCu₅-type structure with a space group of P6/mmm, and the atomic occupations are 1a for R, 2c for Co^I, 3g for Co^II, respectively. The lattice parameters of RCo₅ compounds and the valence bond lengths of R–Co and Co–Co bonds are listed in Table 1. Based on EET, the shortest atomic bond will seriously hamper the magnetization direction, whose density of covalent electron pairs (n_α) is the largest. In Table 1, the valence bond length of Co^I–Co^II is the shortest, which indicates the interactions between Co^I–Co^II is the strongest, and R–Co^I is the second strongest, respectively. As previously reported,^[9] the R–R exchange interaction, which is much weaker than that of R–Co, could be ignored in this calculation. The atomic radii of rare earth elements except for Y element decrease gradually with increasing the atomic number of rare earth element,^[27] which causes the lattice parameters and the valence bond lengths to decrease. The shorter the valence bond length is, the stronger the cohesive energy between the bonded atoms is. As for the abnormal decreases of those parameters in CeCo₅ compound, the cohesive energy might be affected by the mixed valence of Ce-ion (+3, +4).

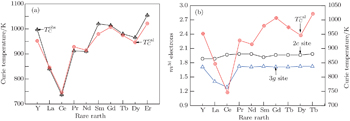
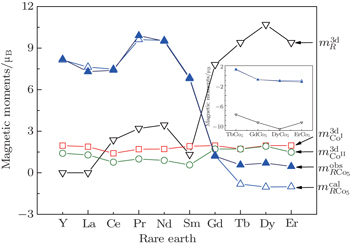
4.2. Calculation of magnetic moment and Curie temperature

The calculated results of magnetic properties are given in Table 2. As shown in Figs. 1 and 2, the calculated results are in good agreement with the experimental results. It reveals that the magnetic moment of Co^I is larger than that of Co^II, which is consistent with the result of neutron diffraction experiment.^[28] The moment of Co^II at 3g is weakened due to the exchange coupling interaction between Co^II at 3g and R at 1a site. According to Fig. 1, it can be found that the moments of RCo₅ are strongly related to those of rare earths. The change tendency of RCo₅ (R is light rare earth) is similar to that of R. However, in the heavy rare earth regime, the two moment curves seem to be axisymmetric due to the negative moment of the heavy rare earth. The change tendencies of Curie temperature of the RCo₅ compounds are related to those of two kinds of Co atoms as shown in Fig. 2, for the heavy rare earth element (HRE) -based RCo₅ are ordered ferrimagnetically. In other words, the 3d magnetic electrons m^3d of LRE in LRECo₅ and YCo₅ compounds exhibit parallel alignment to those of Co while antiparallel in HRECo₅ compounds. The direction of the arranged magnetic electrons in Co atoms is defined as being positive, and that in R atoms is positive in LRECo₅ compounds and it is negative in HRECo₅ compounds. For the HRECo₅ compounds, the 4f electrons contribute to the moment, the molecular moment equals the sum of 3d and 4f moments, which are negative in the calculated results as presented in Eq. (7). It is nicely consistent with the observed result as shown in the inset of Fig. 1. Figure 2 shows the relationships between 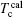and as well as 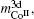where it can be seen that the change tendency of 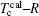curve seems to be similar to that of 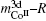curve. It implies that the exchange coupling between Co^I and R affects the Curie temperature of RCo₅. For Co atoms, the moment of Co^I is more than that of Co^II atom. In general, Curie temperatures of RCo₅ are proportional to the average moments per bond number, which reveals the anisotropies of the magnetic exchanging interactions along various bonds. Except for the contribution of 3d–3d or 3d–4f interaction to the ferromagnetic order, the lattice electrons also have an influence on the Curie temperature. As for SmCo₅, the large error between the calculated and observed results for Curie temperature might be caused by the electronic transformations from lattice electrons n_l into 3d magnetic electrons 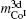at 3g site (see Fig. 3(c)).

	Figure Option View Download New Window
	Fig. 1. Calculated results of magnetic moments of R-, 2c- and 3g-sited Co in RCo₅ compounds. The insert gives the antiferromagnetic interaction between R and Co in RCo₅ compounds when R = heavy rare earth.

	Figure Option View Download New Window
	Fig. 2. (a) Observed and calculated Curie temperatures of RCo₅ and (3d) electron numbers of Co atoms at 2c and 3g sites.

	Figure Option View Download New Window
	Fig. 3. Electronic transformations among all kinds of electrons. The electronic distributions of Co at 2c site (a) and 3g site (b); the electron transformations among the covalence, lattice, 3d magnetic electrons are shown for Co at 2c site (c) and for Co at 3g site (d); the covalence and lattice electrons distributions for Co^I and Co^II are shown in panels (e) and (f).

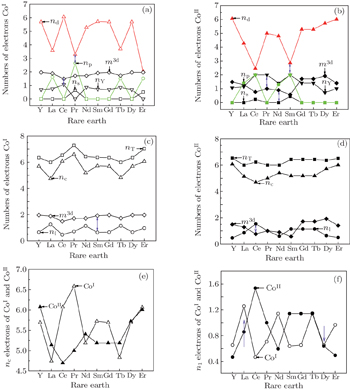
4.3. Analysis of correlation between electronic structure and magnetic property

The calculated valence electronic structures are given in Table 3, and the corresponding electronic transformations are shown in Fig. 3. According to the electron function in electronic binding, the electrons are classified as four categories by EET, which are magnetic electrons, dump pair electrons, lattice electrons, and covalence electrons, denoted by m^3d, n_Y, n_l, and n_c respectively. The so-called dump pair electrons represent either a bonding or an anti-bonding electron with their resulting bonding power mutually canceled by each other. The lattice electron, n_l is empirically introduced as a physical quantity, which comes from s electrons. According to the modern quantum theory, the s electrons might reach an energy level above the Fermi energy if the s energy bandgap is wide. In this case, the electrons can hover in lattice space, therefore the electron is so-called lattice electron. Here, two of the four categories of electrons we are talking about, n_l and n_c, take part in the formation of an atomic bond by electronic transformation. The n_T equals the sum of n_l and n_c.

Figures 3(a) and 3(b) show the electronic transformations among s, p, d, n_Y, and m^3d electrons in Co^I and Co^II atoms, respectively. For either of Co^I or Co^II, the electronic transformation between p and d electrons happens in the form of equivalent electrons. As for the electronic transformation between the m^3d and n_Y electrons, it reveals the correlation between m^3d and d electrons. When the m^3d meets with the d electrons, with their resulting bonding power mutually canceled by each other and their spins are opposite to each other, the electron transformation between m^3d and n_Y occurs. The number variation of m^3d depends upon the electrons transforming from the other electrons into the 3d magnetic electrons. The final numbers of m^3d electrons in Co^I and Co^II atoms make their differences of the contributions to molecular moments and Curie temperature. For Co atoms, the moment of Co^I is bigger than that of Co^II, which is due to the decrease of m^3d electrons induced by electron transformation between m^3d and n_c of Co^I. Figures 3(c) and 3(d) show the electronic transformations between n_l or n_c or n_T and m^3d electrons in Co^I- and Co^II atoms, respectively. The exchange coupling interactions between m^3d and n_l of Co^II in LRECo₅ compounds are the strongest, while those of Co^I- in HRCo₅ compounds are the strongest. Taking CeCo₅ for example, the numbers of n_l in Co^I- is the least and the numbers of n_l in Co^II is the largest, which keep the balance in the final number of n_l. The n_l originates from the s orbital electrons, and s mainly derives from the equivalent p and d electrons. For the HRECo₅ compounds, the 4f electrons also contribute to moments, the molecular moment equals the sum of 3d and 4f moments. Figures 3(e) and 3(f) show that the electronic numbers of n_l and n_c electrons at Co^I and Co^II crystal positions change with the rare earth elements. The changes seem to be the same.

5. Conclusions and perspectives

The empirical electron theory of solids and molecules (EET), which is based on the Pauling’s valance theory, is used to investigate the valence electronic structures and multiple physical properties of solid state materials. The theoretical model is simpler with fewer theoretical parameters than the first principle and the molecular field theory. In this study, the magnetic moments and Curie temperatures of RCo₅ (R = rare earth) intermetallics are systematically studied with EET.

The calculated results reveal that the moments of RCo₅ intermetallics originate mainly from the 3d electrons of Co atoms and 4f electrons of rare earth, the s electrons also affect the magnetic moments by the hybridization of d and s electrons. The contribution to the moment depends on the sublattices of Co and R atoms, and it is found that the moment of Co atom at 2c site is bigger than that at 3g site due to the bonding effect between R and Co associated with a electron transformation from 3d electrons into covalence electrons. In the heavy rare-earth-based RCo₅ intermetallics, the contribution to the molecular moment originates from 3d and 4f electrons. Curie temperatures of RCo₅ are proportional to the average moment along the various bonds, and it indicates the magnetic anisotropy along the various crystal directions. The covalence electrons and lattice electrons also affect the Curie temperature. RCo₅ intermetallic compounds show strong relationships between their valence electronic structure and magnetic properties. Except for the 3d–3d or 3d–4f exchange coupling interaction contributing to the ferromagnetic order, the lattice electrons also affect the Curie temperature.

Reference

1	Larson PMazin I IPapaconstantopoulos D A 2003 Phys. Rev. 67 214405
2	Malik S KArlinghaus F JWallace W E 1977 Phys. Rev. 16 1242
3	Li Z BLan J TZhang X FLiu Y LLi Y F 2015 Chin. Phys. 24 087501
4	Herbst J FHector L G2007J. Alloys Compd.188446
5	Han X FYang F MZeng ZZheng Q QWang X FJin H MSun J Z1997Acta Phys. Sin.(Overseas Edition, i.e., Chin. Phys.)6697
6	Sankar S GRao V U SSegal EWallace W EFrederick W G DGarrett H J 1975 Phys. Rev. 11 435
7	Rao V U SGreedan J E 1973 J. Solid State Chem. 6 387
8	Chen T LWang Q2000Commun. Theor. Phys.346
9	Zhao T SJin H MGuo G HHan X FChen H 1991 Phys. Rev. 43 8593
10	Tadaei IHideaki I2005J. Appl. Phys.9710A313
11	Hector L GHerbst J F 2003 Appl. Phys. Lett. 82 1042
12	Liebs MHummler KBeuerle TUbele PFahnle M1995J. Magn. Magn. Mater.140–144851
13	Miletić G IBlažina Ž 2007 J. Solid State Chem. 180 604
14	Miletić G IBlažina Ž 2009 J. Magn. Magn. Mater. 321 3888
15	Richter MOppeneer P MEschrig HJohansson B 1992 Phys. Rev. 46 13919
16	Beloritzky EFremy M AGavigan J PGivord DLi H S 1987 J. Appl. Phys. 61 3971
17	Hu B PLi H SGavigan J PCoey J M D 1990 Phys. Rev. 41 2221
18	Kokorina E EMedvedev M VNekrasov I A2010International Conference on Magnetic MaterialsOctober 25–29, 2010Kolkata, India75
19	Yu R H1978Chin. Sci. Bull.23217(in Chinese)
20	Cao Z X 2014 Chin. Phys. 23 063102
21	Zhang J FZhang MZhao Y WZhang H YZhao L NLuo Y H 2015 Chin. Phys. 24 067101
22	Fang S SQiao H X 2015 Chin. Phys. 24 083101
23	Guo Y QYu R HZhang R LZhang X HTao K1998J. Phys. Chem. B1029
24	Wu W XGuo Y QLi A HLi W2008Acta Phys. Sin.572486(in Chinese)
25	Meng Z HGuo Y QLi J BWang Y2012Acta Phys. Sin.61107101(in Chinese)
26	Lin CYin G LZhao Y Q 2015 Comp. Mater. Sci. 101 168
27	Shen JQian PChen N X 2004 J. Phys. Chem. Solids 65 1307
28	Givord DDeportes JSchweizer JTasset F 1976 IEEE. Trans. Magn. 12 1000