Cite this Article
Chen Shuang, Su Tie, Zheng Yao-Bang, Chen Li, Liu Ting-Xu, Li Ren-Bing, Yang Fu-Rong. Numerical analysis of quantitative measurement of hydroxyl radical concentration using laser-induced fluorescence in flame. Chinese Physics B, 2016, 25(6): 060703  
Permissions
Numerical analysis of quantitative measurement of hydroxyl radical concentration using laser-induced fluorescence in flame
Chen Shuang1, 2, †, , Su Tie2, Zheng Yao-Bang2, Chen Li2, Liu Ting-Xu2, Li Ren-Bing2, Yang Fu-Rong1, 2
Science and Technology on Scramjet Laboratory, China Aerodynamics Research and Development Center, Hypervelocity Aerodynamics Institute, Mianyang 621000, China
China Aerodynamics Research and Development Center, Mianyang 621000, China

 

† Corresponding author. E-mail: chenshuang827@gamil.com

Project supported by the National Natural Science Foundation of China (Grant No. 11272338) and the Fund from the Science and Technology on Scramjet Key Laboratory, China (Grant No. STSKFKT2013004).

Abstract
Abstract

The aim of the present work is to quantitatively measure the hydroxyl radical concentration by using LIF (laser-induced fluorescence) in flame. The detailed physical models of spectral absorption lineshape broadening, collisional transition and quenching at elevated pressure are built. The fine energy level structure of the OH molecule is illustrated to understand the process with laser-induced fluorescence emission and others in the case without radiation, which include collisional quenching, rotational energy transfer (RET), and vibrational energy transfer (VET). Based on these, some numerical results are achieved by simulations in order to evaluate the fluorescence yield at elevated pressure. These results are useful for understanding the real physical processes in OH-LIF technique and finding a way to calibrate the signal for quantitative measurement of OH concentration in a practical combustor.

PACS: 07.60.Rd;33.80.–b;42.62.–b;42.62.Fi
Keyword:laser-induced fluorescence;hydroxyl radical;quenching;quantitative measurement
1. Introduction

Laser-diagnostic techniques have played an increasing role in combustion research over the last 20–30 years. These techniques are important for detecting temperatures, flow fields and some special species or radical concentration in combustion flow field, because these techniques are nonintrusive and robust. However, despite the rapid development of various techniques based on laser and spectroscopy, the quantitative measurement in the practical combustor is still difficult.

Laser-induced fluorescence (LIF) is probably the most common and important method to measure the densities of some minor species and radicals such as OH, CH, NO, and CO.[1–5] In particular, planar laser-induced fluorescence (PLIF) is more popular due to the high sensitivity, high spatiotemporal resolution. Laser-induced fluorescence relies on the ability to excite molecules or radicals from a ground state to a higher energy state. However, in LIF measurement, the induced fluorescence signal density captured by the intensified-CCD or PMT not only depends on the absolute concentration of the species excited by the laser pulse, but also is related to other processes such as electronic quenching, vibrational energy transfer (VET) and rotational energy transfer (RET).[6–8] These processes are mainly due to the molecular collisional partner, pressure, temperature and quantum state. Then, LIF measurement for quantitative species concentration becomes complex and uncertain in some quasi-practical combustors, such as gas turbine, engine, and other industry facilities. Therefore, it is important and necessary to find the relationship between the fluorescence signal and the real absolute concentrations of species in practical combustion fields.

It should be pointed out that over the years attempts have been made for quantitative measurement of minor species such as OH, NO, and CH. Some collision-insensitive techniques such as saturated LIF[9,10] and the picosecond LIF[11] have been developed to eliminate the influences of quenching, and other techniques combined with LIF and absorption spectroscopy have been used to measure the absolute density directly.[12,13] According to this way a bidirectional laser beam configuration has been demonstrated to be collision independent and self-calibrated for absolute OH number density measurements.[13] But most of the studies using these techniques mentioned above have been carried out in a laboratory-scale burner, which are excellent calibration methods. Therefore to quantitatively measure the OH concentration by LIF, the modeling and analysis on the complex LIF process in high pressure and turbulent flames are still needed. The detailed simulations of OH excitation dynamics have been conducted and continuously developed in recent years, which is conducive to understanding the phenomena in the LIF mechanism.[12,14–17]

In the present work, we analyze the physical processes of OH-LIF diagnostics in flame and make clear the influence of parameters according to pressure. Our goal is to present the real process and evaluate the fluorescence yield in high pressure combustion field, which is important and significant for performing laser diagnostics and quantitative measurement in a practical combustor and facility. In our approach, the phenomena involved in the experimentally measured signal of OH concentration are taken into account as much as possible.

2. Modeling of laser-induced fluorescence

Describing the various processes in LIF experiments accurately is important and critical to achieving the quantitative measurement of radical concentration in high pressure combustion. Another aspect is to obtain a fluorescence signal with high quality and signal-to-noise ratio by some optical strategies and optimized designs, which is not discussed in the current study. We prefer to discuss elementary processes: absorption line shape broadening, collisional transitions and quenching, which are all enhanced when the pressure is augmented.

2.1. Fluorescence signal

Based on the typical LIF experiments and setups,[1] the fluorescent photons per unit of time captured by the photodetectors such as PMT and ICCD, Sf, can be expressed as follows:

where G is the gain of the optical collection system, Ω is the solid angle of collection in unit sr, and V is the probe volume in unit m3. In spite of the fact that the setup and optical layout are easy to calibrate and control, Sf is dependent on the local fluorescent photon number density Np.

Laser-induced fluorescence originates from an interaction process between laser and matter, simply described as a spontaneous light emission that takes place between two quantum states of some species via absorption of a photon with suitable energy. As illustrated in the energy level structure of OH shown in Fig. 1, the big upward arrow means absorption process and the red big downward arrows represent the radiative process, the thin arrows illustrate the processes without radiation, which include collisional quenching, rotational energy transfer (RET) and vibrational energy transfer (VET).[18] The absorption process only takes place due to a certain narrow laser wavelength, but the fluorescence process is a broadband emission.

Fig. 1. Schematic diagram of important energy transfer process in linear OH-LIF.

The fluorescence signal can then be simulated by solving the population rate equations of the states involved.

Following the OH-LIF principle,[18] a laser pulse at wavelength λ according to a given transition between a lower rotational level J″ in vibrational level ν″ of electronic state X2Π and (J′, ν′) of A2Σ+ induces the fluorescence, which is emitted at different wavelengths. In the linear regime of LIF, if a broadband detection scheme including both A2Σ+–X2Π (0, 0) and (1, 1) bands are considered, the relationship is expressed as follows:

where Alaser is the beam area of laser pulse, E is the energy, Φlaser and Φabs are the spectral line shapes of laser and absorption respectively. Then the relationship between the fluorescence signal ratio Sf/EA and the OH density population NOH can be determined by the spectral overlap ∫ ΦlaserΦabs dν, the quantum yield ηf, and the Boltzmann fraction fB. For simplicity and considering various number densities of OH radicals under different pressures, we can remove experimental constants, laser characteristics and transmission efficiency and introduce mole fraction XOH to express the fluorescence signal per unit of absorbing species mole fraction:

2.2. OH structure and dynamic kinetic

The electronic transition (A2Σ+–X2Π) is the most commonly used in OH-LIF diagnostics. Figure 1 is a schematic illustration of this transition. The transition between energy levels of the LIF process has been introduced in Subsection 2.1. The molecules are excited from a rotational level, i, in the vibrational ground state (ν″ = 0) of X2Π to rotational level, j, in either the ground vibrational level (ν′ = 0) or the first excited vibrational level (ν′ = 1) in A2Σ+, which are named OH A–X(0,0) and A–X(1,0) systems respectively. Because of greater predissociation rates, we leave out the excitations to higher vibrational levels in A2Σ+ (ν′ > 1). After that spontaneous emissions compete with molecule collisions, which may cause the molecule to be at a different rotational state within the same vibrational manifold (rotational energy transfer, RET), or to stay at a different vibrational level (vibrational energy transfer, VET). Another main effect of collision is electronic quenching, which is very obvious at high pressure.

In several publications[7,8,12,15,18,19], LIF simulation models have been developed, including these collisional processes describing the detailed dynamics of the levels that are involved. Following Ref. [18], the time-dependent population of a collision-populated rotational level j is described by

Here, Ri j is the state-to-state rate for RET from initial level i to target level j; similarly, Vi j is the state-to-state VET rate, Qj is the quenching rate of level j; Aj and Pj are the Einstein A coefficients for spontaneous emission and the predissociation rate respectively. According to the definitions of VET and RET, Ri j will be zero for all levels that do not belong to the same vibrational level, and Vi j will be zero for all levels that are different vibrational levels.

The quenching, VET and RET-rate are all induced by the collision partner species, and we define collision coefficients as and the partner species number densities as nM. Then the rates in function (4) are described by

The rates are determined by the species and the number densities, therefore the quenching and other collisional effects become stronger at the same mole fraction distribution at higher pressure. In many studies, a simplified two-level system has been obtained. The effective spontaneous emission coefficient Aeff and the effective quenching rate Qeff are adopted and the quenching models and the related collision coefficients are clear.

For electronic transitions in combustion environments at higher pressure than atmospheric, one can assume that the Einstein emission coefficient is much smaller than the collisional quench rate. The fluorescence yield is then approximately equal to

However, in the present work, the simulation considering the detailed collisional effects is very complicated notably because it requires accurate knowledge of VET and RET, and this calculation cannot be dealt with without the help of a systematic model and software such as the LASKIN code.[20] Then we use this software to simulate the change of number densities in different rotational and vibrational levels.

2.3. Others

The structure and the number density distributions of the molecular energy levels are the key to quantitative measurement. It should be specially noted that the ground state of the OH radical has two spin components which give rise to two rotational energy ladders due to spin–orbit interaction. There is an idealized case where a specific coupling between angular momenta is said to be dominant, which is called Hund’s case.[21] We denote the case with subscript 1 or 2 that has the following meaning for the total angular momentum quantum number J:

Here N denotes the rotational quantum number. There is a strong spin–orbit interaction for the low value, which splits an energy level into two ladders as shown in Fig. 2. At high J-levels the spin–orbit interaction becomes weak and the difference in level in F1 and in F2 becomes small. Hund’s coupling case (b) is now a good description of how the angular momenta couple in X2Π, and the quantum number J is replaced by N. The excited state only has one spin component and, as a result, only one rotational energy ladder. The O, P, Q, R, S branches are then labelled by the manifold indices of the upper and lower states.

Fig. 2. Rotational energy levels of the X2Π (ν″ = 0) and A2Σ+ (ν′ = 1) states of OH.
3. Simulation and discussion

It is now important to quantitatively discuss and estimate the aspects that will influence the fluorescence signal and its interpretation based on the laser-induced fluorescence modeling. The fluorescence signal per unit of absorbing species mole fraction depends on the absorption strength (depends on the temperature through the Boltzmann population fraction), the overlap integral (depends on the line broadening), and the fluorescence yield (quenching, VET and RET). These three parameters are examined in this section.

3.1. overlap and broadening

The part ∫ Φlaser(ν)Φabs(ν)dν in function (3) is the spectral overlap of the laser exciting line and the targeted OH absorption line, and depends on the area of the spectral covering of the OH line by the laser line. The typical spectral bandwidths of most commercial lasers (e.g., continuum narrow linewidth dye laser) are 0.3 cm−1 and 0.5 cm−1 and the line shape is constant in the LIF progress.[22]

Based on the complex fine structure of energy levels, the broadening mechanism of absorption line is supported by two main phenomena named collisional broadening and Doppler broadening, which can be expressed as Lorentzian-type and Gaussian-type functions respectively.[23,24] Then the broadening is given by the pressure and translational temperature of the system, and another line shape Voigt is more suitable and widely accepted at high pressure.

The Voigt profile results from the convolutions of the two types of line shapes mentioned before. Theoretically, Doppler broadening depends only on temperature, and the broadening induced by collision is influenced by not only temperature but pressure and composition species. Therefore the Doppler broadening can be calculated in a straightforward manner, but evaluating the collision-induced effects is more complicated and difficult. In terms of the Voigt function, the shape function, (υ −υ0) can be expressed as[24]

where P′ is the normalization constant . Two parameters in Voigt function are and , where ΔυD and ΔυC are the Doppler and collision FWHM respectively. The former ΔυD can be evaluated as ΔυD = 1.7368×10−7T1/2υ0. The collision width is subsumed to be the sum of the contributions of the individual species present in the probe gases. This can be simply expressed as:

where γi is the species-specific pressure-broadening coefficient and pi is the partial pressure of species. The collisional broadening coefficient is usually temperature dependent, and described as

where γ0 is the value at reference temperature, Tref. The coefficient n is the value between 0.1 and −0.1 and depends on the rotational level and collisional partner, which needs to be precisely determined from some special experiments.

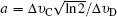
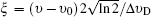
The collisional broadening studies and coefficient measurement of the OH A–X transition at high temperature and pressure environments were performed by Rea et al.,[23] Battles and Hanson[25] for (0,0) band, Kessler et al.,[26] and Atakan et al.[27] for the (1,0) band. In the present study, we do not attempt to accurately measure the coefficients for the collision broadening process. Then for hard-sphere collision theory we adopt the n = −0.66, and parameter a = 0.041.

Assume that the laser is tuned to the center of the absorption line shape. Figure 3 shows the spectral overlaps between the laser and the absorption line P1(7) at different temperatures and pressures ignoring the line shift. Figures 3(a) and 3(b) show the cases of 800 K and 2000 K respectively at elevated pressure, and figure 3(c) shows the broadening due to temperature at 1.0 MPa, and the calculated spectral overlap is presented in Fig. 3(d). As pressure increases, it is also important to consider the absorption line shift induced by collisions. This will influence the laser absorption efficiency because of the offset between the central absorption frequency and the laser line shape. But considering the feasibility of free tuning of the dye laser wavelength in the experiment, only broadening but no shift is calculated in this case.

Fig. 3. Shapes of absorption line P1(7) of OH radicals at 35077 cm−1 at different temperatures and pressures and the line shape of the Nd:YAG-pumped frequency-doubled dye laser: at (a) different pressures and 800 K, (b) different pressures and 2000 K, (c) different temperatures and 1.0 MPa; (d) calculated spectral overlap values.

The results show that as the pressure increases, the spectral overlap decreases because of the collisional broadening of OH absorption line. Secondly, the Doppler broadening increases as the temperature increases and the collisional broadening decreases. As a consequence, the Doppler broadening dominates at low pressure. However, at higher pressure, the collisional broadening dominates, so that the OH absorption line becomes thinner and the spectral overlap increases as the temperature increases. In comparison with the results in Ref. [12], there is some deviation between the exact values of spectral overlap because of the different laser characteristics, but the tendencies in the present work are in accordance with others.

3.2. Boltzmann fraction

According to statistical mechanics, the population distribution of an ensemble of molecules in thermal equilibrium is given by the Boltzmann equation. In laser-induced fluorescence procession, the fluorescence transition is composed of many transitions of OH radicals from the excited vibrational state, and the Boltzmann fraction fB depends on temperature.

The rotational-level populations in the state (ν″ = 0) of X2Π at different temperatures are illustrated in Fig. 4 by using the data from LIFBase.[28] As temperature increases, the rotational energy level J″ with maximum population densities is shifted towards a higher level. It should be noted that the Boltzmann equation is valid only for systems in thermal equilibrium, which means that the translational, electronic, vibrational and rotational modes are equilibrated. This result is helpful to choose the perfect absorption line in such a way that the Boltzmann fraction presents weak variations through the temperature domain. It can also help us confirm the line density to evaluate the fluorescence yield.

Fig. 4. Rotational-level populations in the state (ν″ = 0) of X2Π at different temperatures.
3.3. Quenching, VET and RET

In the present work, for the initial attempt to model the influence of quenching, VET and RET on the LIF signal, we evaluate the fluorescence quantum efficiency under some simple and typical conditions. For the purpose, the burned gases are considered to be a mixture of 72% N2, 19% H2O, and 9% CO2 and the temperature is varied between 800 K and 2000 K at elevated pressure from 0.1 MPa to 1.0 MPa as indicated in the literature.[12]

To evaluate the fluorescence yields at different temperatures and elevated pressure, a lot of groups have made some efforts to build and develop various models based on experiments and simulations. Paul,[7] and Garland and Crosley[29] developed models to simulate the corresponding quenching cross sections as a function of the temperature. Based on and utilizing these published results, Höinghaus et al. built a detailed rate equation model (the LASKIN program packet)[20] for simulating the energy transfer in OH laser-induced fluorescence, which includes all possible state-to-state energy transfer processes such as electronic quenching, VET, RET, depolarization, etc. Then for our case of linear excitation without saturation, the LASKIN code is employed to illustrate the influence of combustion condition on fluorescence efficiency.

In the CH4/air flame, electronic quenching is dominated by H2O and CO2, and sometimes CO is important too. In LASKIN, the quenching cross sections for various collision partners are calculated by using a two-parameter formula which is T-dependent.[18]

The quenching rate for H2O is chosen based on the default value of LASKIN, and the cross section for CO2 is cited from the model of Paul, and the collision of CO is ignored in this case. As mentioned before, Hund’s case (b) notation is used here and the population fractions of spin-split states (F1 and F2) are calculated separately. The important step in the simulation is to calculate the time-dependent populations in the upper-state rotational levels following laser excitation.

Figures 5 and 6 show the population changes at several main levels pumped by the excitation lines P1(7) (0–1) and Q1(6) (0–0) at different temperatures and pressures. The laser pulse shape is defined as a “typical” Nd:YAG-laser pulse with an FWHM of about 5 ns. Considering better comparison, these two excitation lines are chosen in the present work because of the same excited level F1(6). The dominance of the laser-excited level is clear, so is the greater population in the F1 fine-structure components compared with the corresponding F2 components.

Fig. 5. Simulated population densities for several rotational levels in OH (A, v′ = 0) with excitation line P1(7) (0–1) in flame at different temperatures and pressures: (a) 1000 K/0.1 MPa, (b) 2000 K/0.1 MPa, (c) 1000 K/1 MPa, and (d) 2000 K/1 MPa.
Fig. 6. Simulated population densities for several rotational levels in OH(A, v′ = 0) with excitation line Q1(6) (0–0) in flame at different temperatures and pressures: (a) 1000 K/0.1 MPa, (b) 2000 K/0.1 MPa, (c) 1000 K/1 MPa, and (d) 2000 K/1 MPa.

It is clear that the population of the excited level F1(6) decreases at elevated pressure for both excitation lines mainly due to quenching. For the excitation line P1(7) (0–1), the greater population is achieved at higher temperature, which can be explained by the Boltzman fraction and population distribution of the ground level. When increasing temperature, the difference between the levels close to F1(6), such as F1(5)–F1(7) and F2(5)–F2(6)–F2(7), becomes small. At the same time, there is a big gap between these two groups. Thus this tendency is a direct result of the RET in collisions with H2O (i.e., F1–F1 and F2–F2 transitions are more likely than F1–F2 and F2–F1 transitions).[18]

Figure 7 shows the plots of total radiative fluorescence yield of different excitation lines and detected spectral bands (band (0–0) and all). It is obvious that no fluorescence signal is induced from another band out of (0–0) with excitation line Q1(6) (0–0), and the elevated pressure heavily affects the yield of fluorescence. These results illustrate that there is a peak value of temperature with a highest yield at a certain pressure, which can also be explained by the characteristic of RET mentioned above.

Fig. 7. Temperature-dependent relative fluorescence yields of different excitation lines at different temperatures and pressures: (a) P1(7) (0–1) and (b) Q1(6) (0–0). The unit 1 atm = 1.01325×105 Pa.

The LASKIN program packet provides a powerful tool for the modelling of energy transfer in laser-induced fluorescence. But it should be noted that our simulations using LASKIN are not absolutely certain because there are still a lot of uncertainties in collision cross sections for RET, VET and electronic quenching of OH radicals. We hope to achieve better agreement between experimental measurements and theoretical calculations in the next step.

4. Conclusions

The aim of the present work is to achieve quantitative measurement of hydroxyl radical concentration by using laser-induced fluorescence in flame. Therefore, the physical process of OH-LIF diagnostics in flame is analyzed and the various factors determining the detected fluorescence signal are studied numerically. Relative OH concentration can be explained on an absolute scale by calibrating the optical collection constant through using Rayleigh scattering or comparing with calculation results in some simple cases. Consequently, an important effort is devoted to the evaluation of the influences of those parameters on the fluorescence signal. The physical models of spectral absorption line shape broadening, collisional transitions and quenching at elevated pressure are built.

For the typical LIF measurement setup, the relation between the intensity of fluorescence signal and the absolute concentration of OH radicals is described clearly. The fine energy level structure of the OH molecule is illustrated to understand the process of laser-induced fluorescence and others in the case without radiation, which include collisional quenching, rotational energy transfer (RET) and vibrational energy transfer (VET). The quenching, VET and RET-rate are all induced by the collision partner species, and the rates are determined by the species and the number densities, therefore the quenching and other collisional effects become stronger at the same mole fraction distribution under higher pressure.

Based on the detailed physical models built in the present work, some numerical results are achieved by simulations in order to evaluate the fluorescence yield. Firstly, the broadening mechanisms of absorption line are studied and line shape Voigt is accepted in our case of high pressure. The spectral overlap values in a temperature range from 800 K to 2000 K and pressure range from atmosphere to 1.0 MPa are calculated for calibration. Secondly, for a given transition, the population distribution of an ensemble of molecules, which influences the fluorescence signal, is given by the Boltzmann equation. At low temperatures, most of the molecules will be in the ground energy state, while high temperatures will lead to an increase in the probability of finding molecules at higher energy levels.

Most importantly, the simulation of OH LIF with excitation from both excitation lines P1(7) (0–1) and Q1(6) (0–0) is carried out by utilizing the LASKIN program. The transition-dependent quantum yields with different temperatures and various pressures in our certain case are estimated numerically by simulating the time-integrated population distributions. It can be observed that the quenching is a main factor to influence the fluorescence yield especially at elevated pressure significantly. It is worth mentioning that the rates of quenching, VET and RET depend on not only pressure and temperature values, but also the species of production as collision partners.

These results are useful for understanding the real physical processes in OH-LIF technique and finding a way to calibrate the signal for quantitatively measuring OH concentration. The next step of this study is to investigate the fundamental combustion case such as laminar premixed flame in high pressure, develop other quantitative measurement skills and compare experimental results with those from the modeling in order to assess the ability for kinetic mechanisms to modify the parameters of the calibration method. This topic will be studied in the future.

Reference
1Seitzman J MHanson R K1993Planar Fluorescence Imaging in GasesLondonAcademic Press385
2Pfefferle L DGriffin T AWinter M 1998 Appl. Opt. 27 3197
3Bessler W GSchulz CLee TJeffries J BHanson R K 2003 Appl.Opt. 42 4922
4McMillin B KPalmer J LHanson R K 1993 Appl. Opt. 32 7532
5Lee M PMcMillin B KPalmer J LHanson R K 1992 J. Propulsion Power 8 729
6Kohse-Höinghaus K 1994 Prog. Energy Combust. Sci. 20 203
7Paul P H 1994 J. Quantum Spectrosc. Radiat. Transfer 51 511
8Bailey A EHeard D EHenderson D APaul P H 1999 Chem. Phys. Lett. 302 132
9Carter C DSalmon J TKing G BLaurendeau N M 1987 Appl. Opt. 26 4551
10Desgroux PDomingues ECottereau M J 1992 Appl. Opt. 31 2831
11Köllner MMonkhouse PWolfrum J 1990 Chem. Phys. Lett. 168 355
12Matynia AIdir MMolet JRoche Cde Persis SPillier L 2012 Appl. Phys. B: Lasers Opt. 108 393
13Arnold ABombach RKäppeli BSchlegel A 1997 Appl. Phys. B: Lasers Opt. 64 579
14Yin ZAdamovich I VLempert W R 2013 Proc. Combust. Inst. 34 3249
15Yin Z YCarter C DLempert W R 2014 Appl. Phys. 117 707
16Matynia AMolet JRoche CIdir Mde Persis SPillier L 2012 Combust. Flame 159 3300
17Schießl RMaas UHoffmann AWolfrum JSchulz C 2004 Appl. Phys. B: Lasers Opt. 79 759
18Kienle RLee MPKohse-Höinghaus K 1996 Appl. Phys. B: Lasers Opt. 62 583
19Battles B EHanson R K 1995 J. Quantun Spectrosc. Radiat. Transfer 54 521
20Rahmann UBulter ALenhard UDusing RMarkus DBrockhinke AKohse-Höinghaus K“LASKIN — A Simulation Program for Time-Resolved LIF-Spectra”Internal Report, University of Bielefeld, Faculty of Chemistry, Physical Chemistry I http://pc1.uni-bielefeld.de/textascii˜laskin
21Herzberg G1950Molecular spectra and molecular structure I: Spectra of diatomic molecules2nd edn.TorontoD. van Nostrand Company Inc.
22Singla GScouflaire PRolon CCandel S 2006 Combust. Flame 144 151
23Rea E CChang A YHanson R K 1989 J. Quantum Spectrosc. Radiat. Transfer 41 29
24Hwang S MKojima J NNguyen Q VRabinowitz M J 2008 J. Quantun Spectrosc. Radiat. Transfer 109 2715
25Battles B EHanson R K 1995 J. Quantun Spectrosc. Radiat. Transfer 54 521
26Kessler W JAllen M GDavis S J 1993 J. Quantun Spectrosc. Radiat. Transfer 49 107
27Atakan BHeinze JMeier U E 1997 Appl. Phys. B: Lasers Opt. 64 585
28Luque JCrosley D R1999“LIFBASE”, SRI International Report MP 99-009
29Garland N LCrosley D R1986Proc. Combust. Inst.211693