Cite this Article
Wu Yan-Qiu, Cai Li, Wu Hong-Juan. Analyses of an air conditioning system with entropy generation minimization and entransy theory. Chinese Physics B, 2016, 25(6): 060507  
Permissions
Analyses of an air conditioning system with entropy generation minimization and entransy theory
Wu Yan-Qiu†, , Cai Li, Wu Hong-Juan
Chongqing Three Gorges University, Chongqing 404100, China

 

† Corresponding author. E-mail: wuyanqiu0516@126.com

Project supported by the Youth Programs of Chongqing Three Gorges University, China (Grant No. 13QN18).

Abstract
Abstract

In this paper, based on the generalized heat transfer law, an air conditioning system is analyzed with the entropy generation minimization and the entransy theory. Taking the coefficient of performance (denoted as COP) and heat flow rate Qout which is released into the room as the optimization objectives, we discuss the applicabilities of the entropy generation minimization and entransy theory to the optimizations. Five numerical cases are presented. Combining the numerical results and theoretical analyses, we can conclude that the optimization applicabilities of the two theories are conditional. If Qout is the optimization objective, larger entransy increase rate always leads to larger Qout, while smaller entropy generation rate does not. If we take COP as the optimization objective, neither the entropy generation minimization nor the concept of entransy increase is always applicable. Furthermore, we find that the concept of entransy dissipation is not applicable for the discussed cases.

PACS: 05.70.Ln
Keyword:entropy generation;entransy increase;entransy dissipation;optimization analyses;finite time thermodynamics;air conditioning system
1. Introduction

Air conditioning systems are widely used in many buildings. The analyses and optimizations of air conditioning systems have attracted more and more attention because they are very important for energy conservation and the reduction of cost.[1–10] In order to improve the system performance and increase the energy utilization, some optimization theories have been developed, such as the entropy generation minimization[11] and the entransy theory.[8]

The entropy generation minimization has been widely used in the analyses and optimizations of thermal systems.[12–17] In air conditioning systems, this theory has also been applied.[18,19] However, some researchers further found that the entropy generation minimization does not always lead to the optimal performances for different optimization objectives. For example, when the refrigeration capacity is not fixed, Klein and Reindl[20] found that minimizing the entropy generation rate does not always result in the same design as maximizing the system performance, and when larger heat flow into the high temperature heat source is the objective, the entropy generation minimization is not always applicable, either.[8]

The entransy theory was proposed by Guo et al.[21] for heat transfer and it has been widely applied to analyzing heat transfer processes.[21–32] This theory has also been extended to the analyses of thermodynamic processes.[33–36] Cheng and Liang[33] defined a new concept of entransy loss rate. For the discussed systems, it was shown that the entransy loss rate maximum results in the output power maximum.

For the heat pump system, Chen et al.[18] applied the entropy concept to its optimization. But Klein and Reindl[20] found that the entropy generation rate minimum does not always result in the best system performance. So the discussion of the applicability of the entropy generation minimization to the heat pump systems is still necessary. Recently, Cheng and Liang[8,10,19] used the entransy theory to analyze air conditioning systems. They found that the concept of entransy increase is applicable for the analyses of the heat flow into the high temperature heat source. However, there are not many papers on the analyses of air conditioning systems with the entransy theory. Further investigations are still necessary.

In this paper, based on the generalized heat transfer law, an air conditioning system is analyzed with the entransy theory and the entropy generation minimization. The coefficient of performance (denoted as COP) and the heat flow rate Qout which is released into the high temperature heat source are taken as the optimization objectives, and the applicabilities of the entropy generation minimization and the entransy theory to the optimizations are also discussed.

2. Entransy theory and entropy generation minimization

In the analogy between the electrical and heat conductions, Guo et al.[21] noted that the thermal system lacks the parameter corresponding to the electrical potential energy. With this consideration, they proposed the concept of entransy, which can be expressed as[36,37]

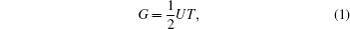
where U is the internal energy and T is the temperature. It is shown that this concept can describe the potential energy of heat in an object, and reflect the thermal energy of thermomass for the object.[37] In practical heat transfer, it was proved that there always exists entransy dissipation.[20,38] With the concepts of entransy, entransy flow and entransy dissipation, the principle of least action and the entransy balance equation in heat transfer can be obtained.[37] Then, the extremum entransy dissipation principle and the minimum entransy dissipation based thermal resistance principle for heat transfer were developed and applied to the analyses and optimizations of many heat transfer processes.[21–32,36–44]

Furthermore, Cheng and Liang[33] and Cheng et al.[34] proposed the concept of work entransy, with which the entransy balance equation for thermodynamic cycles can be set up. Then, the concept of entransy loss was developed.[33] For a thermodynamic system, it was shown that entransy loss is the difference between the entransy flows that get into and out of the system, and the consumed entransy.[33,37] When there is no work done in the thermodynamic system, the thermodynamic system becomes a heat transfer system, and the entransy loss equals the entransy dissipation.[37] Cheng and Liang[33] found that larger entransy loss leads to larger output work when some conditions are satisfied. In some application cases, the concept of entransy loss was found to be effective for the analyses and optimizations of some thermodynamic systems.[33–37,45–48]

However, some researchers[49,50] thought that the entransy theory was a copy of the entropy generation minimization, or gave the same optimization results as those of the entropy generation minimization. In heat transfer and thermodynamic cycles, many comparisons showed that the two theories are different.[22–24,33,34,37] We also did some work on the analyses of an endoreversible Carnot heat engine with the entransy theory and the entropy generation minimization.[51] The results showed that the two theories are not the same, and the major problems in Ref. [51] were pointed out. In the present work, this issue will also be discussed in the analyses of an air conditioning system.

3. The discussed air conditioning system

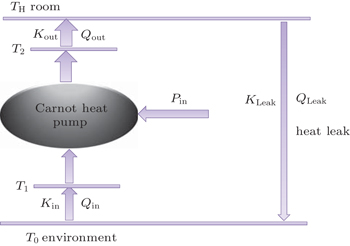
The discussed air conditioning system is shown in Fig. 1.[8]

Fig. 1. An air conditioning system.

In this system, the heat flow rate Qin, which is from the environment at temperature T0, flows into the Carnot heat pump, which works between temperatures T1 and T2. During the cycle, the input power is Pin, and the heat flow rate Qout is released to the room at temperature TH. The heat leak rate QLeak between the environment and the room is considered.

We assume that the heat transfer processes satisfy the generalized heat transfer law,[52–55] there are

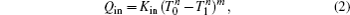
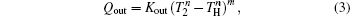
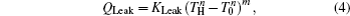
where m and n are constants, Kin is the product of the heat transfer area and the corresponding heat transfer coefficient between the environment and the working fluid of the reverse Carnot cycle, Kout is the product of the heat transfer area and the corresponding heat transfer coefficient between the working fluid of the reverse Carnot cycle and the room, and KLeak is the product of the heat transfer area and the corresponding heat transfer coefficient between the room and the environment.

Considering the energy conservation, there is

According to the Carnot theorem, we have

The system COP is

The entropy generation rate Sg of this system is[37]

According to the definition of entransy increase rate Ginc, we can obtain[8]

The entransy dissipation rate Gdis is[56]

4. Numerical examples and discussion

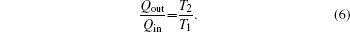
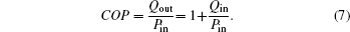
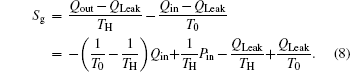
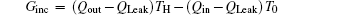
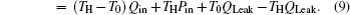
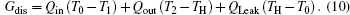
Taking COP and Qout as the optimization objectives, we analyze the relationships of COP, Qout, Sg, Ginc, and Gdis below. Five cases will be calculated numerically.

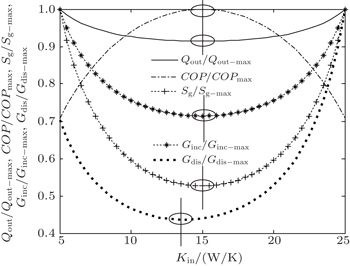
In the first case, we assume that TH = 300 K, T0 = 275 K, and Qin = 200 W. When m = n = 1, the heat transfer law is the Newton heat transfer law. With this law, we assume KLeak = 0.8 W/K and Kin + Kout = 30 W/K. As Kleak, Kin, and Kout are the products of the heat transfer areas and the corresponding heat transfer coefficients, their values depend on the size of the heat pump and the corresponding heat transfer performance. So, the values may be different for different heat pumps. In this paper, the data are set to be close to those in Ref. [8]. With Eqs. 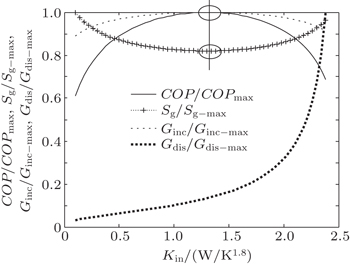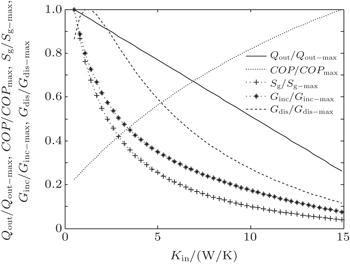(2)–(10), the variations of COP, Qout, Sg, Ginc, and Gdis with Kin can be shown in Fig. 2.

Fig. 2. Variations of COP, Qout, Sg, Ginc, and Gdis with Kin when Qin is fixed and m = n = 1.

It can be seen that COP reaches its maximum value for Kin = 15.0 W/K, while Qout, Sg, and Ginc reach their minimum values. However, Gdis reaches neither its minimum value nor its maximum value at the same point. Furthermore, we can calculate two more heat transfer laws. When we assume that m = 1.2, n = 1.5, KLeak = 1 × 10−2 W/K1.8, and Kin + Kout = 2 W/K1.8, the variations of COP, Qout, Sg, Ginc, and Gdis with Kin can be shown in Fig. 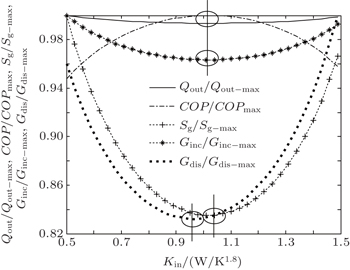3. When we assume that m = 1, n = 5, KLeak = 0.8 × 10−10 W/K5, and Kin + Kout = 3 × 10−9 W/K5, the variations of COP, Qout, Sg, Ginc, and Gdis with Kin can be shown in Fig. 4. From Figs. 2–4, we can find that the variation tendencies of COP, Qout, Sg, Ginc, and Gdis in Figs. 3 and 4 are the same as those in Fig. 2.

Fig. 3. Variations of COP, Qout, Sg, Ginc, and Gdis with Kin when Qin is fixed, m = 1.2 and n = 1.5.
Fig. 4. Variations of COP, Qout, Sg, Ginc, and Gdis with Kin when Qin is fixed, m = 1 and n = 5.

In this case, Qin, TH, T0, and QLeak are all given. We can find that the variation tendencies of Qout, Sg, and Ginc are the same as that of Pin in Eqs. (5), (8), and (9). Furthermore, equation (7) shows that COP and Pin have opposite variation tendencies, with Qin fixed. These are the reasons why the curves behave in the way shown in Figs. 2–4 when Qin, TH, T0, and QLeak are prescribed.

As above, we show that both the entropy generation minimization and the entransy increase minimization lead to the maximum COP in this case. On the other hand, if larger Qout is our objective, larger entransy increase rate leads to larger Qout, while smaller entropy generation rate does not. This conclusion is consistent with that obtained by Cheng and Liang[8] when they analyzed a heat pump system with the concepts of entropy generation and entransy increase. Furthermore, our results show that the concept of entransy dissipation is not applicable for the optimizations, and this conclusion is consistent with that obtained by Cheng et al.[37,55] when they reviewed the entransy theory.

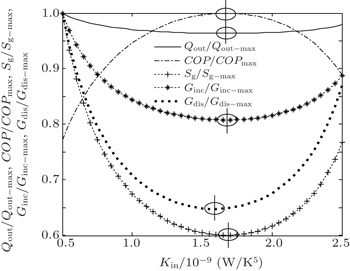
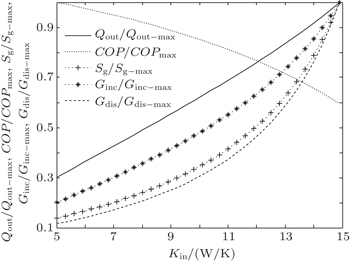
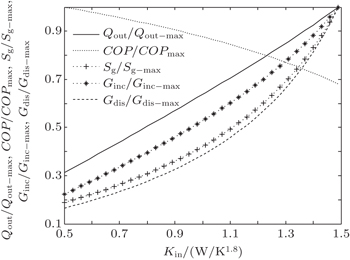
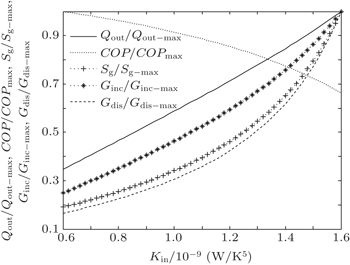
In the second case, we assume that TH = 300 K, T0 = 275 K, and Pin = 300 W. With Eq. (6), we can find that COP is proportional to Qout, with Pin fixed, which means that the variation tendencies of COP and Qout are the same. So, we will not calculate Qout below. Considering that the heat transfer laws may be different, the three heat transfer laws discussed in the first case are also analyzed here. When m = n = 1, we assume that KLeak = 1 W/K and Kin + Kout = 25 W/K. With Eqs. (2)–(10), the variations of COP, Sg, Ginc, and Gdis with Kin can be shown in Fig. 5, which shows that COP and Ginc both reach their maximum values for Kin = 12.6 W/K, while Sg arrives at its minimum value. At the same point, Gdis reaches neither its minimum value nor its maximum value.

Fig. 5. Variations of COP, Sg, Ginc, and Gdis with Kin when Pin is fixed and m = n = 1.

When m = 1.2 and n = 1.5, we assume that KLeak = 1 × 10−2 W/K1.8 and Kin + Kout = 2.5 W/K1.8. When m = 1 and n = 5, we assume that KLeak = 1 × 10−10 W/K5 and Kin + Kout = 2.5 × 10−9 W/K5. For these two heat transfer laws, the variations of COP, Sg, Ginc, and Gdis with Kin are shown in Figs. 6 and 7, respectively. The variation tendencies of COP, Qout, Sg, Ginc, and Gdis in Figs. 6 and 7 are the same as those in Fig. 5. For different heat transfer laws, our results show that both the entropy generation minimization and the entransy increase maximization lead to the maximum values of Qout and COP. In this case, the concept of entransy dissipation is not applicable.

Fig. 6. Variations of COP, Sg, Ginc, and Gdis with Kin when Pin is fixed, m = 1.2 and n = 1.5.
Fig. 7. Variations of COP, Sg, Ginc, and Gdis with Kin when Pin is fixed, m = 1 and n = 5.

In the third case, we assume that TH = 300 K, T0 = 275 K, and T1 = 265 K. The three heat transfer laws are also discussed here. We assume that KLeak = 0.5 W/K and Kin + Kout = 20 W/K for m = n = 1, KLeak = 5 × 10−2 W/K1.8 and Kin + Kout = 2 W/K1.8 for m = 1.2 and n = 1.5, and KLeak = 5 × 10−11 W/K5 and Kin + Kout = 2 × 10−9 W/K5 for m = 1 and n = 5, respectively. For the three heat transfer laws, the variations of COP, Qout, Sg, Ginc, and Gdis with Kin can be shown in Figs. 8–10, respectively. The numerical results show that the variation tendencies of Qout, Sg, Ginc, and Gdis are the same, and they all increase monotonically with increasing Kin, while COP decreases monotonically. For this case, if we take Qout as the optimization objective, the numerical results show that larger values of entransy increase rate and entransy dissipation rate lead to the larger Qout, while smaller entropy generation rate does not. If we take COP as the optimization objective, we can find that the entropy generation minimization, entransy increase minimization and entransy dissipation minimization all lead to a maximal COP.

Fig. 8. Variations of COP, Qout, Sg, Ginc, and Gdis with Kin when T1 is fixed and m = n = 1.
Fig. 9. Variations of COP, Qout, Sg, Ginc, and Gdis with Kin when T1 is fixed, m = 1.2 and n = 1.5.
Fig. 10. Variations of COP, Qout, Sg, Ginc, and Gdis with Kin when T1 is fixed, m = 1 and n = 5.

In the fourth case, we assume that TH = 300 K, T0 = 275 K and T2 = 325 K. For the three heat transfer laws, we assume that KLeak = 1 W/K and Kin + Kout = 20 W/K when m = n = 1, KLeak = 0.1 W/K1.8 and Kin + Kout = 2 W/K1.8 when m = 1.2 and n = 1.5, and KLeak = 1 × 10−10 W/K5 and Kin + Kout = 2 × 10−9 W/K5 when m = 1 and n = 5, respectively. The variations of COP, Qout, Sg, Ginc, and Gdis with Kin are also shown in Figs. 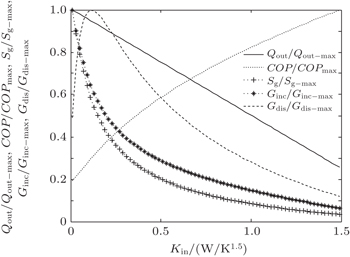11–13, respectively. The results show that there is a maximum value for Gdis, but there are no extremum values for COP, Qout, Sg, and Ginc. Qout, Sg, and Ginc all decrease monotonically with increasing Kin, while COP increases monotonically. Therefore, if COP is our optimization objective, the entropy generation minimization and entransy increase minimization both lead to the maximum COP. If larger Qout is our objective, only larger entransy increase rate results in larger Qout, while smaller entropy generation rate does not. The concept of entransy dissipation is not applicable for the analyses for this case, either.

Fig. 11. Variations of COP, Qout, Sg, Ginc, and Gdis with Kin when T2 is fixed and m = n = 1.
Fig. 12. Variations of COP, Qout, Sg, Ginc, and Gdis with Kin when T2 is fixed, m = 1.2 and n = 1.5.
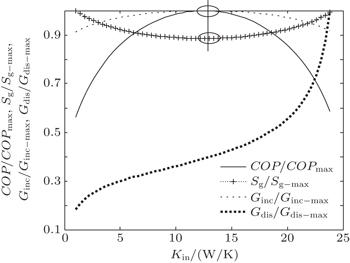
Fig. 13. Variations of COP, Qout, Sg, Ginc, and Gdis with Kin when T2 is fixed, m = 1 and n = 5.

In the fifth case, we assume that TH = 300 K, T0 = 265 K, T1 = 263 K, and T2 = 320 K. According to Eqs. (5) and (6), we can obtain

Then, we have

Therefore, with Eqs. (7) and (12), there is

It can be seen that COP is constant in this case. For the three heat transfer laws, we assume that KLeak = 2 W/K when m = n = 1, KLeak = 6 × 10−2 W/K1.8 when m = 1.2 and n = 1.5, and KLeak = 1.7 × 10−10 W/K5 when m = 1 and n = 5, respectively. The variations of COP, Qout, Sg, Ginc, and Gdis with Kin can be shown in Figs. 14–16, respectively.

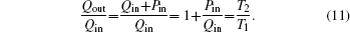
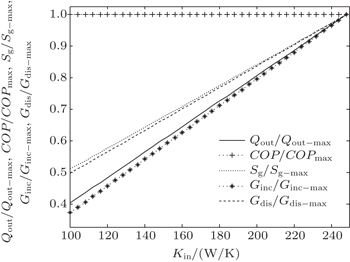Fig. 14. Variations of COP, Qout, Sg, Ginc, and Gdis with Kin when T1 and T2 are fixed and m = n = 1.
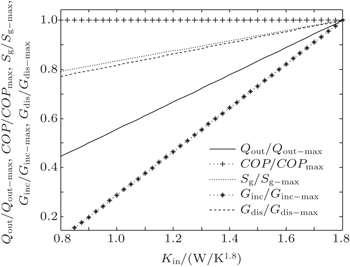Fig. 15. Variations of COP, Qout, Sg, Ginc, and Gdis with Kin when T1 and T2 are fixed, m = 1.2 and n = 1.5.

The results show that Qout, Sg, Ginc, and Gdis all increase monotonically with increasing Kin. Therefore, larger entransy dissipation rate, larger entropy generation rate, and larger entransy increase rate all lead to larger Qout. For the analyses of COP, none of the concepts of entransy dissipation, entransy increase and entropy generation are applicable.

Fig. 16. Variations of COP, Qout, Sg, Ginc, and Gdis with Kin when T1 and T2 are fixed, m = 1 and n = 5.
5. Conclusions

In this paper, the applicabilities of the entropy generation minimization and the entransy theory to the optimization analysis of an air conditioning system are discussed. Three different heat transfer laws and five cases are analyzed numerically.

The applicabilities of the entransy theory and the entropy generation minimization to the discussed air conditioning system are conditional. If larger Qout is the objective, larger Ginc always leads to larger Qout, while smaller entropy generation does not. If COP is taken as the optimization objective, neither the entropy generation minimization, nor the entransy increase minimization (or maximization) nor the entransy dissipation minimization (or maximization) always leads to the maximum COP.

For the five discussed cases, the concept of entransy dissipation is not applicable for the optimizations of COP nor Qout.

Reference
1Wang HWu G X 2013 Chin. Phys. 22 087501
2Cheng X TLiang X G 2015 Chin. Phys. 24 060510
3Wang W HCheng X TLiang X G 2013 Chin. Phys. 22 110506
4Cheng X TZhang Q ZXu X HLiang X G 2013 Chin. Phys. 22 020503
5Zhao X LFu LZhang S G 2011 Energy Convers. Manage 52 494
6Chen L GFeng HSun F R 2011 J. Energy Institute 84 105
7Bi YChen L GSun F R 2009 Int. J. Exergy 6 550
8Cheng X TLiang X G 2013 Chin. Sci Bull. 58 4696
9Li JChen L GGe Y LSun F R 2013 Acta Phys. Sin. 62 130501 (in Chinese)
10Cheng X TLiang X G 2014 Energy Convers. Manage 80 238
11Myat AThu KKim Y D 2011 Appl. Therm. Engineering 31 2405
12Cheng X TLiang X G 2013 Chin. Phys. 22 010508
13Adavbiele A S 2010 Int. J. Energy Research Africa 1 67
14Chen L GWu C HSun F R 1999 J. Non-Equil. Thermody. 24 327
15Wu C HChen L GChen J C1999Recent Advances in Finite Time ThermodynamicsNew YorkNova Science Publishers
16Chen L GSun F R2004Advances in Finite time thermodynamics: Analysis and OptimizationNew YorkNova Science Publishers
17Myat AThu KKim Y D 2011 Appl. Thermal Eng. 31 2405
18Chen L GFeng HSun F R 2011 J. Energy Institute 84 105
19Cheng X TLiang X G 2013 Energy Buildings 67 387
20Klein S AReindl D T 1998 J. Energy Resources Technology 120 172
21Guo Z YZhu H YLiang X G 2007 Int. J. Heat Mass Transfer 50 2545
22Cheng X TLiang X G 2011 Int. J. Heat Mass Transfer 54 269
23Cheng X TZhang Q ZLiang X G 2012 Appl. Thermal Eng. 38 31
24Cheng X TLiang X G 2012 Energy Convers. Manage 58 163
25Chen L GXiao Q HXie Z HSun F R 2012 Int. Comm. Heat. Mass Transfer 39 1556
26Chen L GFeng H JXie Z HSun F R 2013 Int. J. Heat Mass Transfer 67 704
27Chen L GXiao Q HXie Z HSun F R 2013 Int. J. Heat Mass Transfer 67 506
28Chen L GWei S HSun F R 2014 Int. J. Low-Carbon Tech. 9 20
29Feng H JChen L GSun F R 2012 Sci. China: Tech. Sci. 55 779
30Feng H JChen L GXie Z HSun F R 2014 Sci. China: Tech. Sci. 57 784
31Feng H JChen L GXie Z HSun F R 2014 Chin. Sci. Bull. 59 2470
32Liu WLiu Z CJia HFana A WNakayama A 2011 Int. J. Heat Mass Transfer 54 3049
33Cheng X TLiang X G 2012 Energy 44 964
34Cheng X TChen QHu G JLiang X G 2013 Int. J. Heat Mass Transfer 60 180
35Açikkalp E 2014 Energy Convers. Manage 86 792
36Hu G JCao B YGuo Z Y 2011 Chin. Sci. Bull. 56 2974
37Cheng X TLiang X G 2014 Chin. Sci. Bull. 59 5309
38Cheng X TLiang X GGuo Z Y 2011 Chin. Sci. Bull. 56 847
39Xia S JChen L GSun F R 2010 Appl. Math. Model. 34 2242
40Chen L G 2012 Chin. Sci. Bull. 57 4404
41Chen L G 2014 Sci. China: Tech. Sci. 57 2305
42Feng H JChen L GXie Z HSun F R 2015 Sci. China: Tech. Sci. 58 1084
43Feng H JChen L GXie Z HSun F R 2015 Int. J. Heat Mass Transfer 84 848
44Feng H JChen L GXie Z HSun F R 2015 Int. J. Heat Mass Transfer 89 24
45Yang A BChen L GXia S JSun F R 2014 Chin. Sci. Bull. 59 2031
46Zhu YHu ZZhou YJiang LYu L 2014 Energy Convers. Manage 88 267
47Li TFu WZhu J 2014 Energy 72 561
48Kim K HKim K 2015 Int. J. Heat Mass Transfer 84 80
49Bejan A 2014 ASME J. Heat Transfer 136 055501
50Oliveira S RMilanez L F. 2014 Int. J. Heat Mass Transfer 79 518
51Wu Y Q 2015 Chin. Phys. 24 070506
52Cheng X TLiang X G 2013 Energy Convers. Manage 73 121
53Chen LGLi JSun F R 2008 Appl. Energy 85 52
54Xia S JChen L GSun F R 2008 J. Therm. Sci. Tech. 7 226
55Cheng X TWang W HLiang X G 2012 Sci. China: Tech. Sci. 55 2847
56Cheng X TLiang X G 2014 Energy Convers. Manage 87 1052