Cite this Article
Shi Rong-Hua, Xiao Yi, Shi Jin-Jing, Guo Ying, Lee Moon-Ho. Anonymous voting for multi-dimensional CV quantum system. Chinese Physics B, 2016, 25(6): 060301  
Permissions
Anonymous voting for multi-dimensional CV quantum system
Shi Rong-Hua1, Xiao Yi1, Shi Jin-Jing1, †, , Guo Ying1, Lee Moon-Ho2
School of Information Science & Engineering, Central South University, Changsha 410083, China
Institute of Information & Communication, Chonbuk National University, Chonju 561-756, Korea

 

† Corresponding author. E-mail: shijinjing@csu.edu.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 61272495, 61379153, and 61401519), the Research Fund for the Doctoral Program of Higher Education of China (Grant No. 20130162110012), and the MEST-NRF of Korea (Grant No. 2012-002521).

Abstract
Abstract

We investigate the design of anonymous voting protocols, CV-based binary-valued ballot and CV-based multi-valued ballot with continuous variables (CV) in a multi-dimensional quantum cryptosystem to ensure the security of voting procedure and data privacy. The quantum entangled states are employed in the continuous variable quantum system to carry the voting information and assist information transmission, which takes the advantage of the GHZ-like states in terms of improving the utilization of quantum states by decreasing the number of required quantum states. It provides a potential approach to achieve the efficient quantum anonymous voting with high transmission security, especially in large-scale votes.

PACS: 03.67.–a;03.67.Dd;03.67.Hk
Keyword:quantum cryptography;anonymous voting;quantum entangled state;continuous variable
1. Introduction

Quantum cryptography has arisen over the last decades centering on the manipulation of individual quanta of information, known as quantum bits or qubits.[1,2] Based on physical laws instead of mathematical complexities, communication with perfect secrecy can be guaranteed in an insecure channel in Vernam’s sense of one-time pad known as quantum cryptography.[3,4] Quantum entanglement (QE)[5,6] is one of its characteristics which plays a greatly vital role in quantum cryptography. It reflects the relevance of quantum bits, which has won the support of the local hidden-variable theory. Quantum cryptography is widely used in many active fields such as quantum signature, secret sharing, voting, and so on.[7–9]

Voting is a behavior that often takes place in democratic society. The traditional voting would not well meet the present voting demands because of its weakness, such as low efficiency and insecurity. With the development of network and cryptography techniques,[10] electronic voting (E-voting) arises at a historic moment. Based on cryptography, E-voting requires computers and networks to realize voting functions. E-voting also has the advantages of high efficiency, convenience and flexibility, which has been applied to several research areas.[11–13] With the continual expanding of ballot activities, scholars all over the world are actively exploring and designing secure ballot schemes. However, E-voting schemes could be easily broken by the emergence of quantum computers. Thus quantum cryptography can be applied in voting to realize the unconditional security and detectable eavesdropping,[14] which brings both challenges and opportunities to ballot protocols. In particular, the unique physical characteristic QE arouses wide concern, and how to apply it in ballots to design more secure and stable quantum ballot schemes has become an important issue in secure communications. Hillery et al. presented a fair voting protocol based on quantum resources.[15] Vaccaro et al. introduced kinds of quantum protocols for anonymous voting and their surveying.[16] Shi et al. proposed a quantum distributed ballot scheme based on Greenberger–Horne–Zeilinger (GHZ) state.[17] Those proposals are all of importance in the situations that the identity of the person who sends the message should be secret.[18–20] Unfortunately, there are still challenges for the security if talking of collaborating parties cannot be prohibited, the voting message of each individual voter may be learnt by the tallyman or the other voters.

The quantum cryptography with continuous variable (CV)[21,22] has the strength of security and high efficiency.[23,24] The CV-based quantum voting protocols were proposed,[25] which employed Einstein–Podolsky–Rosen (EPR) pairs to serve as information carrier and introduced a new idea of utilizing CV quantum states during the voting procedure. It demonstrates that CV-based quantum cryptography can improve the practicality of quantum voting. The protocols of Ref. [25] can not only bring the conception of CV quantum voting but also offer us more opportunities to study more efficient voting schemes. Considering the voting efficiency, we suggest anonymous communications[26] and two quantum anonymous voting protocols (QAVP) based on a quantum cryptosystem with multidimensional CV, in which CV-based GHZ-like states[27–30] are applied as information carriers. The GHZ-like states employed as voting states in this paper consist of momentum-squeezed and position-squeezed modes. All the modes are taken advantage of in the voting process, which indicates that the proposed protocols can not only guarantee the security of communications but also improve the voting efficiency by decreasing the required consumption of GHZ-like states. The remainder of this paper is organized as follows. Section 2 introduces QAVP with continuous variable entangled states (CVES). The security and efficiency are analyzed in Section 3 respectively. Finally, the conclusions are drawn in Section 4.

2. Quantum anonymous voting protocols

First, the QAVP should obey the following principles:

P1 A voter should have no knowledge of any other voter’s votes.

P2 The tallyman could only acquire the collective votes while having no access to individual voters’ votes.

P3 The votes should be receipt-free. It means it is impossible for a voter to prove how he/she votes for a third party, even if he/she wants to.

P4 A voter can only vote once, meanwhile, the value of each vote should only be counted once.

Then a CVES-based quantum voting scheme and two improved protocols with modified operators are introduced respectively.

2.1. A CVES-based quantum scheme

To satisfy the above-mentioned principles, we start with a fundamental QAVP, which can be divided into two parts, i.e., the preparation and voting phase, and measurement of the final states.

2.1.1. Preparation and voting phase

During the voting procedure, the tallyman cannot gain any information about the individual votes from voters, which can be achieved by utilizing an entangled state to carry the voting information. With a map S, the CV-based GHZ-like state[31] with three modes (1, 2, and 3) serving as the information carrier can be expressed in Heisenberg operators, i.e.,

where the matrix S can be written as

More explicitly, the GHZ-like state can be expressed as

where for ∀ k ∈ {1,2,3} stand for position-squeezed (momentum-squeezed) vacuum modes. The superscript “(0)” denotes initial vacuum modes and “r” denotes squeezing parameters (a dimensionless effective interaction time).[23] The voting operation can be defined as a displacement operation, i.e.,

Operation on the mode k is denoted with the subscript k, while α and β (real numbers) indicate the displacement on position and momentum respectively.

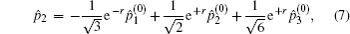
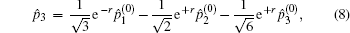
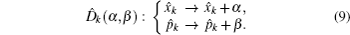
Suppose two candidates Alice and Bob are involved, and n voters participate in the voting process. Then the voting phase depicted in Fig. 1 can be described as follows.

Fig. 1. The binary-valued ballot with the CV-based GHZ-like states. i ∈ {1,2,3…,n} and the subscript “2/3” denotes the operation on mode 2 or mode 3. VM stands for voting mode (we can choose mode 2 or mode 3). VM’ denotes the state on mode 2/3 when all the voters have completed the voting.

Step 1 Distribution of the prepared modes A group of CV-based GHZ-like state denoted in Eq. (1) is distributed: the tallyman keeps mode 1 and the remaining mode 2 and mode 3 are sent to the ballot agency.

Step 2 Voting for the candidates The i-th voter applies an operation on the voting mode (mode 2 or mode 3) to vote for one candidate (Alice or Bob) or does nothing to vote for the other candidate (Bob or Alice).

Step 3 Measuring the displacement and deriving voting result Not until all the n voters complete their voting could the tallyman measure the overall displacements to count Alice’s vote nAlice, while Bob’s vote nBob can be achieved from nAlice and the number n of all voters, i.e., nBob = n − nAlice.

2.1.2. Measurement of the final states

The tallyman’s duty is to measure the final state to obtain the voting result, that is, the number of each kind of votes should be published. The tallyman can implement measurements on different final states where the voting with position operations differs from that with momentum operations. Next, two kinds of measurements, position measurement and momentum measurement are discussed.

However, there is a situation where some participants may cheat or give up voting, which cannot be ignored. Thus two improved protocols are presented as follows.

2.2. Two improved protocols with modified operators

A modified displacement operation on mode 2 and mode 3 is applied to propose two improved voting protocols, i.e., a simple binary-valued ballot protocol with two candidates and multi-valued ballots with m candidates. Thus a refined displacement operator can be expressed as

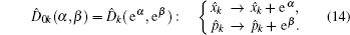
Here α and β are arbitrary real numbers. Voters can adjust the value of α or β to vote.

2.2.1. CV-based binary-valued ballot

The binary-valued ballot is a special case of anonymous voting, in which the vote is required to be a binary natural number. This binary-valued ballot is considered beneficial for the vote procedure involving two candidates (Alice and Bob), and each voter can vote for just one of them. Quantum anonymous voting is involved in the binary-valued ballot as well. Either the position-squeezed mode or momentum-squeezed mode could serve as an ideal voting mode. Since the above-mentioned measurements are relatively similar, only the position-squeezed mode is taken into consideration in this part. This voting process presented in Fig. 2 contains 3 steps.

Fig. 2. The improved binary-valued ballot with the CV-based GHZ-like state. j ∈ {1,2,3…,n} and k ∈ {2,3}.

Step 1 Preparation and distribution of the initial modes The CV-based GHZ-like state in Eq. (1) is employed as the initial ballot state. The mode 1 is kept by the tallyman while mode 2 and mode 3 are distributed to the ballot agency.

Step 2 Voting Ballot agency is provided for the voters to register their votes. Voters have two choices, Alice or Bob. The j-th voter applies a displacement operation in Eq. (14) on mode 2 (3) to vote Alice (Bob). Suppose there are in total n voters and j ∈ {1,2,3…,n}. Then the mode 2 or mode 3 becomes

In Eqs. (15), and (16), vj is the value of the j-th voter’s vote and it completely depends on the voter’s option. Given a one-time vote, vj should be taken as a constant value, v0 for instance. Then each voter could exercise their rights of voting smoothly.

Step 3. Measurement of the final states In order to derive the voting result, position measurement is implemented. After all voters complete their voting, the tallyman collects mode 2 and mode 3, i.e., and , which can be expressed as

Then the tallyman detects the position of the whole three modes and transforms them to the classic results x1, and . Thus he can work out the numbers nAlice (nBob) of Alice’s (Bob’s) vote. It is assumed that r in Eq. (2) satisfies r → ∞, thus the numbers of Alice’s vote and Bob’s vote could be described as

The sum of the two candidates’ votes above and the amount of voters should be numerically equal, i.e., nAlice+nBob = n. Otherwise, it means that someone involves the cheating strategy and the whole voting procedure is invalid. However, if r is a finite large value, the result is different, and an error should be taken into consideration. Therefore, equations (19) and (20) should be transformed to

Considering the determinacy and unambiguity of the ballot result, the error should be less than 0.5. Thus, v0 acquires a limitation: . Furthermore, the numbers nAlice, nBob may not be integers with respect to the inaccurate measurement and the introduced error. So they should be rounded to the nearest integer and discussed as before. If nAlice+nBob ≠ n, there may be someone cheating in the voting.

2.2.2. CV-based multi-valued ballot

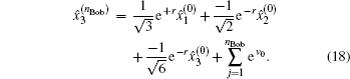
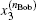
Another ballot, multi-valued ballot is introduced, in which voters have m (m > 2) choices corresponding to m candidates (denoted as Cm). It is discussed in this part that one group of CV-based GHZ-like states could offer four choices (position-squeezed modes and momentum-squeezed modes are all utilized) for voting. Four situations where m may refer to 4t, 4t − 1, 4t − 2, 4t − 3 (t = 1,2,3,…) should be considered. The first situation: m = 4t is discussed only, since the differences for the four situations exist in the employing of the position or momentum of the two modes, and the analysis of these four situations are almost the same. Also, n voters and the ballot agency are involved in the ballot. The voting process presented in Fig. 3 contains three steps.

Fig. 3. Multi-valued ballot with the CV-based GHZ-like state, where j ∈ {1,2,3…,n}, i ∈ {1,2,3…,t}, α and β are arbitrary real numbers.

Step 1 Preparation and distribution of the initial modes Since the number of candidates in this multi-valued ballot is more than two, t groups of CV-based GHZ-like states are employed here. The tallyman keeps all the first modes and (i ∈ {1,2,…, t} is the group number), and the remaining modes , , , and are sent to the ballot agency.

Step 2 Voting The modified displacement operation is acted on the initial states. It is assumed that the j-th, k-th, p-th, and q-th voters want to vote for the (4i − 3)-th candidate C4i−3, the (4i − 2)-th candidate C4i−2, the (4i − 1)-th candidate C4i−1, and the 4i-th candidate C4i respectively. They apply the displacement operations , , , and on the position and momentum of the second and the third mode of the i-th group respectively, i.e.,

For only one vote, vj, vk, vp, and vq are all set to v0. Voting for other candidates just needs to repeat this kind of operation as Eqs. (23)–(26).

Step 3 Measurement of the final states When all the voters complete voting, the tallyman collects all the modes and detects their positions and momenta. Then he reduces all the modes to classic results. Again, two situations should be considered: r → ∞ or r is a finite large value. When r → ∞, the number of votes for the candidates C4i−3, C4i−2, C4i−1, and C4i can be shown as

Then it can be determined whether voters have cheated during the voting by matching the voters’ and votes’ amount. If , it demonstrates that there is no cheating strategy. Otherwise, the voting is invalid. In another case that r takes a finite large value, the error should be taken into consideration, which is analogous to Eq. (21) and Eq. (22).

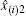
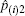
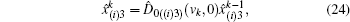
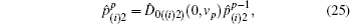
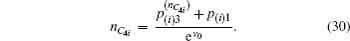
Besides, another case that a voter may give up voting should be considered. If a voter gives up voting while another voter votes twice, the cheating behavior cannot be detected with the previous method in Subsection 2.1. However, the problem could be solved by setting the option of giving up voting as the (m+1)-th choice. The exact number for the voters who give up voting can be obtained definitely.

Next, the security and efficiency of the improved protocols are discussed.

3. Security and Efficiency Analysis
3.1. Security analysis

During the voting process, cheating behavior is unpopular. The two most possible cheating behaviors occurring in the voting phase can be discussed as follows.

Case 1 Voting more than once In the fundamental protocol in Subsection 2, only two modes of the CV-based GHZ-like state are consumed. The number of Alice’s votes is obtained by when mode 2 serves as the voting mode, and the number of Bob’s votes can be achieved by

However, the voter may cheat by voting more than once. Suppose there are k voters supporting for Alice, and each of them excepts the i-th voter who implements to vote for Alice m times. Then the number of Alice’s votes can be expressed as instead of the correct result, where the superscript “(c)” signifies the appearance of cheating behavior. Recording both kinds of votes as mentioned in Subsubsection 2.2.1 can solve this problem, since all the three modes of the CV-based GHZ-like state are involved, where . The cheating behavior can be detected by the sum of nAlice and nBob. If the equation of nAlice+nBob = n is satisfied, there is no cheating behavior during voting, otherwise, the voting is invalid. Thus the cheating behavior of voting more than once can be detected definitely.

Case 2 Conspiracy of cheating At the very beginning of Subsection 2.1, a displacement operation of is employed to operate on the voting mode. However, a situation in which a dishonest participant may cheat cannot be ignored. Suppose that a dishonest participant Eve is about to cheat, and she wants to vote for Alice twice by applying on the mode 2 and on the mode 3 if she has access to both. Even if not, she can still connive with another dishonest voter Clair who may be tempted easily. If Eve takes an operation of on the mode 2 and Clair operates on the mode 3, they can vote for Alice four times together and reduce Bob’s votes by once simultaneously. In order to prohibit this kind of cheating, a modified displacement operator is introduced in Eq. (14). The properties of exponential function in the complex operator are effective to prohibit cheating behavior. Since α and β are arbitrary numbers, once they are changed, the result is different. Corresponding to the above assumption, Eve may operate on mode 2 and Clair may operate on mode 3, if other voters operate normally, the mode 2 and mode 3 could be rewritten as

The value of e4v0 in Eq. (32) differs from that of e−v0 in Eq. (33), thus it is determined that , and the conspiracy fraud can be clearly detected. Thus the problem of conspiring to cheat can be solved with the improved operator .

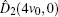
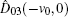
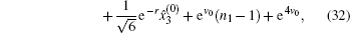
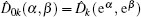
The security of the proposed protocols is proved by analyzing the performance for detecting the two most possible cheating behaviors above. With the modified operator and CV-based GHZ-like states, cheating behaviors can be prohibited effectively.

3.2. Efficiency analysis

For the purpose of ensuring the security and confidentiality, the CV-based GHZ-like states are utilized as quantum resources in our proposed protocols, which contributes to deriving an effective voting scheme with high utilization of quantum states as well.

In the CV-based multi-valued ballot protocol, t (t ≥ 1) groups of CV-based GHZ-like states are employed, and each group can provide four modes (the position-squeezed and momentum-squeezed mode of mode 2 and those of mode 3) to serve as voting modes. It is merely required to prepare two groups of CV-based GHZ-like states if there are eight candidates. Generally, it is defined that 4t candidates could require t groups of CV-based GHZ-like states in our protocols. 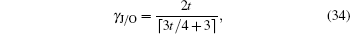The comparison of the quantities that CV-based GHZ-like states consumed in our protocols and EPR states consumed in Jiang’s protocol is shown in Table 1. The consumption ratio γJ/O of consumed quantum modes between Jiang’s protocol and ours can be expressed as

where the denominator rounds up to an integer. It denotes that the utilization of quantum modes in our protocols differs from that of Jiang’s protocol with different values of t. If t = 1,2,3, the quantities of consumed CV-based GHZ-like states and EPR states are almost the same or with small differences in the two schemes, as well as the quantities of consumed quantum modes, while if t → ∞, γJ/O → 8/3. It demonstrates that a potential efficient voting protocol with high utilization of quantum states can be achieved with CV-based GHZ-like states.

Table 1.

Comparison of the quantities that CV-based GHZ-like states and EPR states consumed in our protocols and Jiang’s protocol[25] respectively during the voting process. “CN”, “QCG”, “QCE”, and “QCM” are abbreviated for “candidates’ number”, “quantities of consumed GHZ-like states”, “quantities of consumed EPR states”, and “quantities of consumed quantum modes”, respectively.

.
4. Conclusions

Two branches of anonymous voting, CV-based binary-valued ballot and CV-based multi-valued ballot, are proposed in this paper, in which CV-based GHZ-like states are utilized to complete the voting process with less waste of consumed states. Each voter’s anonymity and privacy can be guaranteed by the entanglement of CV-based GHZ-like states. The improved displacement operation is introduced to ensure the principle P4, i.e., voters cannot vote more than once and conspire with others. It demonstrates that the improved protocols can realize the anonymous voting with high utilization of quantum states, which provides a potential approach to increase the voting efficiency with transmission security as well.

Reference
1Christian WStefano PRaul G PNicolas J CTimothy C RJeffrey H SSeth L 2012 Rev. Mod. Phys. 84
2Radchenko I VKravtsov K SKulik S PMolotkov S N 2014 Laster Phys. Lett. 11 065203
3Gisin NRibordy GTittel W 2001 Rev. Mod. Phys. 74 145
4Jouguet PElkouss DKunz-Jacques S 2014 Phys. Rev. 90 042329
5Gou L DWang X Q 2015 Acta Phys. Sin. 64 070302 (in Chinese)
6Zhang S LWang KGuo J SShi J H 2015 Chin. Phys. Lett. 32 070302
7Boiron DFabbri ALarré P ÉWestbrook C KZiń P 2015 Phys. Rev. Lett. 115 025301
8Maitra ADe S JPaul GPal A K 2015 Phys. Rev. 92 022305
9Rahaman RParker M G 2015 Phys. Rev. 91 022330
10Shi R HSu QGuo YHuang D Z 2013 Int. J. Theor. Phys. 52 376
11Chaum D1998Lecture Notes in Computer ScienceBerlinSpringer-Verlag17710.1007/3-540-45961-8
12Ashouri-Talouki MBaraani-Dastjerdi A 2014 International Journal of Multimedia and Ubiquitous Engineering 9 361
13Zuo LKumar NTu HSingh AChilamkurti NRho S 2014 Journal of Supercomputing 70 177
14Bao NHalpern N Y2015Doklady Mathematics89290arXiv:1501.00458v1
15Hillery MZiman MBužek VBieliková M 2006 Phys. Lett. 349 75
16Vaccaro J ASpring JChefles A 2007 Phys. Rev. 75 012333
17Shi R HWu YGuo YZeng G H 2010 Commun. Theor. Phys. 54 257
18Christandl MWehner S2005Lecture Notes in Computer ScienceBerlinSpringer-Verlag21710.1007/3-540-45961-8
19Wang J X 2014 Acta Phys. Sin. 63 184203 (in Chinese)
20Lu HChen L B 2015 Chin. Phys. 24 070307
21Gong L HSong H CHe C SLiu YZhou N R 2014 Phys. Scr. 89 035101
22Ottaviani CSpedalieri GBraunstein S LPirandola S 2015 Phys. Rev. 91 022320
23Braunstein S LLoock P V 2005 Rev. Mod. Phys. 77 513
24Walk NRalph T CSymul TLam P K 2013 Phys. Rev. 87 020303
25Jiang LHe G QNie DXiong JZeng G H 2012 Phys. Rev. 85 042309
26Yang MLuo J ZLing ZFu X WYu W 2015 IEEE Commun. Mag. 53 60
27Greenberger D M 1990 Am. J. Phys. 58 1131
28Eisert JPlenio M B 2003 Int. J. Quantum Inform. 1 479
29Yan YZou JWang LXu B MWang C QShao B 2015 Commun. Theor. Phys. 63 149
30Wang MXiang YHe QGong Q 2015 Phys. Rev. 91 012112
31Loock P VBraunstein S L 2000 Phys. Rev. Lett. 84 3482