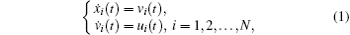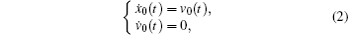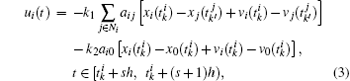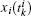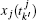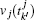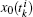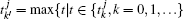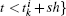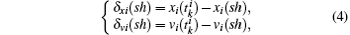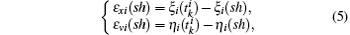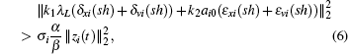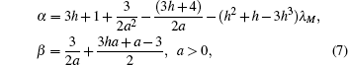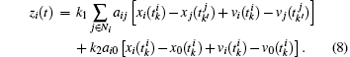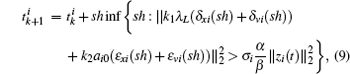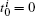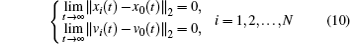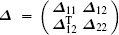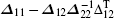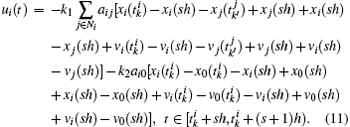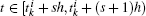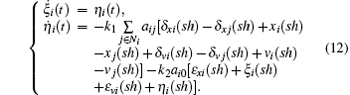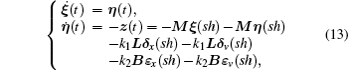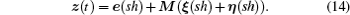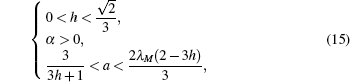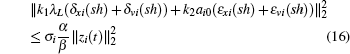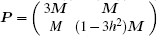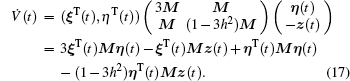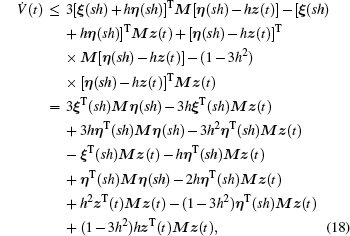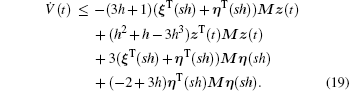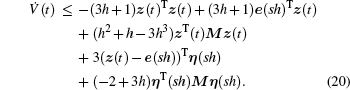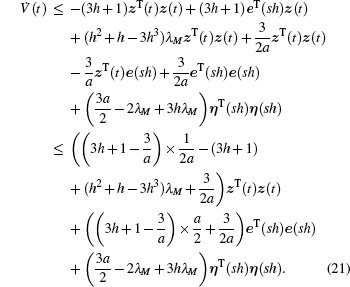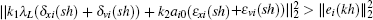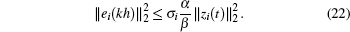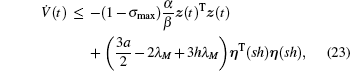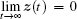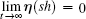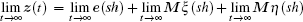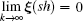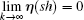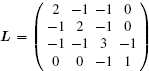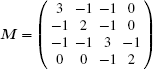Cite this Article
Cao Jie, Wu Zhi-Hai, Peng Li. Distributed event-triggered consensus tracking of second-order multi-agent systems with a virtual leader. Chinese Physics B, 2016, 25(5): 058902  
Permissions
Distributed event-triggered consensus tracking of second-order multi-agent systems with a virtual leader
Cao Jie, Wu Zhi-Hai†, , Peng Li
Key Laboratory of Advanced Process Control for Light Industry of the Ministry of Education, School of Internet of Things Engineering, Jiangnan University, Wuxi 214122, China

 

† Corresponding author. E-mail: wuzhihai@jiangnan.edu.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 61203147, 61374047, and 61403168).

Abstract
Abstract

This paper investigates the consensus tracking problems of second-order multi-agent systems with a virtual leader via event-triggered control. A novel distributed event-triggered transmission scheme is proposed, which is intermittently examined at constant sampling instants. Only partial neighbor information and local measurements are required for event detection. Then the corresponding event-triggered consensus tracking protocol is presented to guarantee second-order multi-agent systems to achieve consensus tracking. Numerical simulations are given to illustrate the effectiveness of the proposed strategy.

PACS: 89.75.–k;05.65. + b;02.30.Yy;
Keyword:consensus tracking;event-triggered control;sampled-data;second-order multi-agent systems;
1. Introduction

In the last decade, synthesis and analysis of multi-agent systems have been extensively investigated by various researchers from multiple disciplines due to their broad applications, including swarming, flocking,[1] formation, target pursuit,[2,3] synchronization,[4] automated highway systems, distributed sensor networks, cooperative control of unmanned air vehicles, congestion control in communication networks, and so on. As one of the basic issues in the distributed coordination control of multi-agent systems, consensus is to design an appropriate control protocol for each agent such that the whole system can ultimately reach an agreement.[5–12]

Along with the progress in computer technology, an agent may be equipped with an embedded microprocessor to access information and update the control input. However, since the power supply of an agent is constrained, it is urgent for researchers to devise a proper consensus algorithm for multi-agent systems such that the energy consumption can be further reduced while the control performance is guaranteed. From this respect, two alternatives are in consideration to make the control updating more efficient. A traditional method is the time-triggered control, in which the control execution and information transmission are periodic. Although this approach is effective for energy saving to some extent, the sampling period is often chosen according to the worst-case scenario, which may lead to unnecessary energy waste. Motivated by this conflict, the event-triggered strategy has been subsequently proposed. In event-triggered fashion, controller actuation only happens at some specific instants rather than continuously or in a periodic pattern. These specific instants are determined by a predefined event condition, e.g., the error exceeds a specific threshold. It was shown in Ref. [10] that the event-triggered control outperforms the time-triggered control in many aspects.

Recently, there has been a remarkable rise in the amount of results on event-triggered control of networked control systems and wireless networks.[13–17] This framework has been proved to be applicable for multi-agent systems in Ref. [18]. Based on the idea of feedback, Dimos et al. proposed both centralized and distributed event-triggered strategies for each agent to determine the control updates. In Ref. [19], Garcia et al. revised the event condition to avoid continuous communication on the basis of the results in Ref. [18]. Two novel event-based control strategies applying a time-dependent event detector for average consensus of single-integrator and double-integrator multi-agent systems were presented in Ref. [20]. In Ref. [21], Fan et al. considered the event-triggered consensus problems of the first-order multi-agent systems, where the event condition involves combinational measurements to further reduce the controller actuation. In Ref. [22], a novel event-based control algorithm was proposed to solve the consensus problem of multi-agent systems with switching topologies, in which the event condition is distributed and sampled.

In essence, the focus of event condition contains two factors: lower frequency of control updating and less information transmission among agents. However, when it comes to a consensus tracking case, conditions are more complicated than those in the average consensus case. Recently, there were some studies on event-triggered consensus tracking of multi-agent systems. In Ref. [23], the consensus tracking problems in multi-agent systems with and without communication delays were considered, where the follower and the leader are assumed to be a single-integrator and a double-integrator, respectively. In Ref. [24], a distributed event-triggered control strategy for the second-order multi-agent systems was proposed, where the control input incorporates continuous measurement of the leader. In Ref. [25], an event-triggered strategy and a distributed estimation were proposed for the dynamic tracking control of the second-order multi-agent systems, where the communication among agents needs to be carried out constantly. In Ref. [26], Li et al considered the event-triggered consensus tracking of the second-order multi-agent systems with fixed and switching topologies, where the high-frequency control updating happens if the states of the agents are close.

In the above references[23–26] about event-triggered consensus tracking of multi-agent systems, there is a common fact that the event condition is assumed to be continuously examined, which implies a great amount of energy waste. Motivated by this observation, we propose a novel distributed event-triggered consensus tracking strategy, where continuous information is replaced with sampled data in event detection for lower communication. It is shown that the parameters of the event condition can be selected such that the second-order multi-agent systems achieve consensus tracking.

The remainder of this paper is organized as follows. Section 2 briefly introduces some concepts in algebraic graph theory and states the problem. Section 3 presents convergence analysis of the event-triggered consensus tracking protocol. In Section 4, numerical simulations are given to illustrate the effectiveness of our results. Section 5 draws conclusions and discusses further research directions.

2. Preliminaries and problem statement
2.1. Algebraic graph theory and some notations

The interaction topology of multi-agent systems can be modeled by an undirected graph G = (V, E, A), which consists of a vertex set V = {v1, v2,⋯, vN} representing N agents, an edge set E ⊆ V × V representing the communication links among agents, and a weighted adjacency matrix A = [aij]. An edge between vi and vj is denoted by eij = (vi, vj). The adjacency element aij associated with the edge eij is positive, i.e., eij ∈ E ⇔ aij > 0. Moreover, we assume aii = 0 for all i ∈ I. For an undirected graph G, the adjacency matrix A is symmetric, i.e., aij = aji. The set of neighbors of vertex vi is denoted by Ni = {vj ∈ V: eij ∈ E}. Correspondingly, the degree matrix D of G is defined as D = diag(d1,d2,…, dN) with di = ∑j∈Niaij. The Laplacian matrix of G is denoted by L = D − A. A path from vi to vj means a sequence of distinct edges (vi,vi + 1), (vi + 1,vi + 2), …, (vi + l,vj) in a graph. If there is a path between vi and vj, then vi and vj are called connected. Graph G is connected if and only if there is a path between any two vertices. An important fact of L is that all row sums are zero and thus L has a right eigenvector 1N associated with the zero eigenvalue, i.e., L1N = 0N, where 1N and 0N denote the N-dimensional column vectors with all ones and zeros, respectively. If graph G is connected, L has one and only one zero eigenvalue and the remaining eigenvalues of L are all positive.

The following notations will be used throughout this paper. RN means the N-dimensional Euclidean space. For a vector x ∈ RN, its Euclidean norm is denoted as ∥x∥2. For a matrix A ∈ RN × N, the transpose matrix and the largest eigenvalue of A are denoted as AT and λA, respectively. A > 0 or A < 0 represents that the matrix A is positive definite or negative definite, respectively.

2.2. Problem statement

Consider second-order multi-agent systems consisting of N agents and one virtual leader. The dynamics of agents can be described as

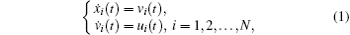
where xi(t) ∈ R, vi(t) ∈ R, and ui(t) ∈ R represent the position state, the velocity state, and the control input of agent i, respectively.

The dynamics of the virtual leader can be described as

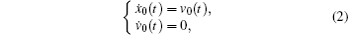
where x0(t) ∈ R and v0(t) ∈ R are the position and velocity states of the virtual leader, respectively.

Denote the sampling period and the k-th event time of agent i by h and 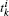, respectively. It should be pointed out that the initial purpose of introducing the event-triggered mechanism to multi-agent systems is to reduce the frequency of control updating along with communication between neighboring agents. For this purpose, we introduce sampled-data into event condition design. At first, we propose the event-triggered consensus tracking protocol for agent i as follows:

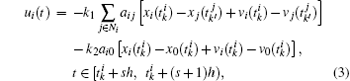
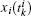
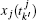
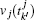
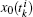
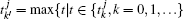
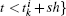
where the position state and the velocity state represent the last measurements transmitted by agent i, the position state and the velocity state represent the last measurements received from the neighbor agent j, the position state and the velocity state represent the last measurements received from the virtual leader, k1 > 0 and k2 > 0 are two control gains to be determined later, , ,ai0 = 1 if agent i has access to the virtual leader, and ai0 = 0 otherwise.

Since the errors play preliminary roles in an event, we define the state error measurements and tracking error measurements of agent i as

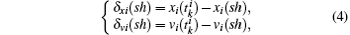
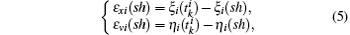
where ξi(t) = xi(t) − x0(t) and ηi(t) = vi(t) − v0(t).

Based on the above definitions, we can further propose the following event condition:

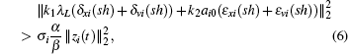
where 0 < σi < 1, the parameters α and β are defined as

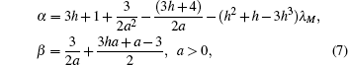
and

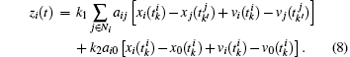
Remark 1 At each sampling instant, each agent has to check the event condition to determine whether an event is triggered. Once the condition (6) is satisfied, agent i updates its control law (3) and notifies its neighbors to substitute its information with current state , otherwise no further action is required. On the other hand, both kinds of errors given by Eqs. (4) and (5) are reset to zero at every event instant. Thereby, the next event instant can be accordingly defined as follows:

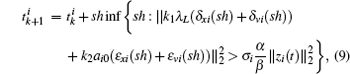
where is the initial instant. Since the event condition of agent i remains invariant during a sampling period, the inter-event times can be lower bounded by sampling period h, that is, the event instant is an integer multiple of h. Thus, Zeno-behavior is absolutely excluded.

Definition 1 The second-order multi-agent systems (1) with the virtual leader (2) are said to achieve consensus tracking if

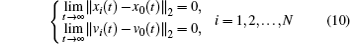
holds for any initial conditions.

In the following, we will theoretically and numerically show the effectiveness of the protocol (3) with the condition (6) to guarantee the systems (1) with the virtual leader (2) to achieve consensus tracking. Before moving on, we need the following assumption and lemmas.

Assumption 1 The network topology composed of N agents and a virtual leader is fixed and undirected, and there is a path from the virtual leader to each agent.

Lemma 1 Let H = L + B, where B = diag{a10,a20 ⋯,aN0} and ai0 is defined as above. If Assumption 1 is satisfied, H must be a positive definite matrix.[27]

Lemma 2 Consider a symmetric matrix 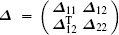, where Δ11 and Δ22 are square. Then Δ is positive definite if and only if both 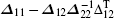and Δ22 are positive definite.[28]

3. Convergence analysis

In this section, we will theoretically show the effectiveness of the protocol (3) with the condition (6) to guarantee the systems (1) with the virtual leader (2) to achieve consensus tracking. Before moving on, we first change the control input (3) of agent i into the following form:

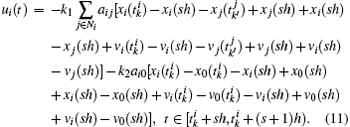
Referring to the definitions of errors given in Eqs. (4) and (5), the dynamics of agent i for 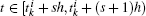can be described as

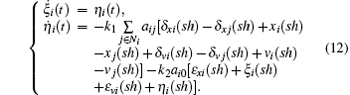
Denoting M = k1 L + k2 B, we can obtain Mξ(sh) = k1 Lx(sh) + k2Bξ(sh) and Mη(sh) = k1 Lv(sh) + k2 Bη(sh). Equation (12) can be rewritten in a compact form as

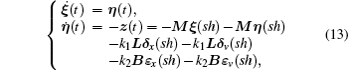
where ξ(t) = (ξ1(t),…,ξN(t))T, η(t) = (η1(t),…,ηN(t))T, δx(t) = (δx1(t),…,δxN(t))T, δv(t) = (δv1(t),…,δvN(t))T, εx(t) = (εx1(t),…,εxN(t))T, εv(t) = (εv1(t),…,εvN(t))T, and z(t) = (z1(t),…,zN(t))T. To reduce the clutter in the notations, we denote e(sh) = − k1 Lδx(sh) − k1 Lδv(sh) − k2 Bεx(sh) − k2 Bεv(sh). Then we have

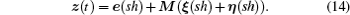
Now we provide the main results.

Theorem 1 Under Assumption 1, the second-order multi-agent systems (1) with the virtual leader (2) applying the consensus tracking protocol (3) with the event condition (6) can asymptotically achieve consensus tracking, if

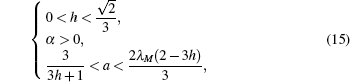
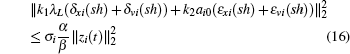
are satisfied simultaneously.

Proof Take a candidate Lyapunov function V(t) = wT(t)Pw(t)/2, where w(t) = (ξT(t),ηT(t))T and the matrix P is chosen as .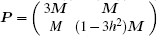

Recalling Lemma 1 and Lemma 2, we have and Δ22 = (1 − 3h2)M. From Eq. (15), it is easy to know that the matrix P is positive definite. Then the time derivative of V(t) along the trajectory generated by Eq. (13) for any t ∈ [sh, (s + 1)h) is presented as

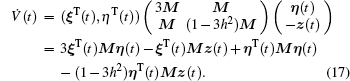
Applying the Taylor expansion of ξ(t) and η(t) at t = sh, we obtain

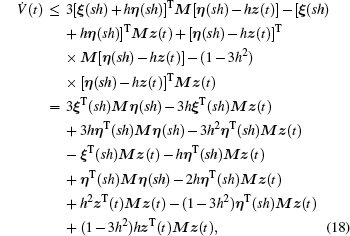
which further leads to

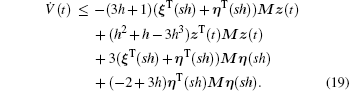
By using Eq. (14) for simplification, we can derive

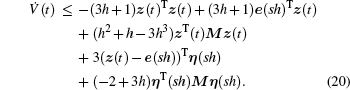
Considering Eq. (15) and the inequality xTLy ≤ axTLx/2 + yTLy/2a, a > 0, we have

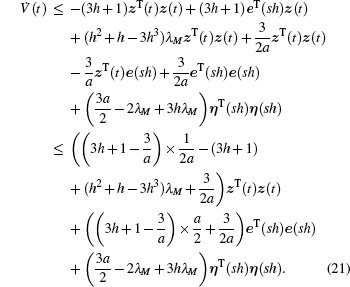
From Eq. (16) and 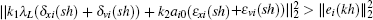, we can easily derive the following inequality:

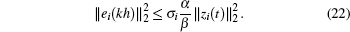
Thus, the function V̇(t) can can be bounded as follows:

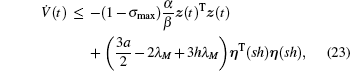
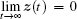
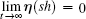
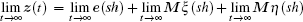
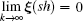
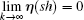
where σmax = max{σi|i = 1,…, N}. From Eq. (23), it is obvious that V̇(t) is negative semi-definite for k ∈ {0,1,2,…} and t ∈ [sh, (s + 1)h] as z(t)Tz(t) ≥ 0 and ηT(sh)η(sh) ≥ 0. Since V(t) > 0, V̇(t) ≤ 0, we can obtain , which further leads to and . It follows from Eq. (22) that , which implies that and . Thus, the proof of Theorem 1 is completed.

Remark 2 In this paper, the network topology is assumed to be undirected. It should be noted that the results of this paper can be extended to the directed network topology case. For the directed network topology case, Assumption 1 needs to be changed into the assumption that the network topology composed of N agents and a virtual leader is fixed and directed, there is a spanning tree, and the virtual leader is the root node of the spanning tree.

Remark 3 Note that our method contains several noticeable advantages over existing works. Firstly, different from centralized condition, our event condition is distributed, that is, each agent has its own event condition to determine when to update control input. Secondly, the event condition proposed in Eq. (6) is composed of sampled-data, which is effective for further reducing energy consumption. In such strategy, the event examination for each agent happens in a periodic pattern, while most works are in continuous time. Thirdly, different from results in Ref. [23]–[26], where each agent needs to access the information of neighbors constantly, the continuous communication between neighboring agents can be avoided due to introduction of zi(t) into event design. Finally, in Ref. [23]–[25], the velocity information of the virtual leader is always required as a necessary part of event condition for each agent, however, this requirement is unnecessary in the event detection given by Eq. (6).

Remark 4 It should be pointed out that in order to compute the event condition in Eq. (6), each agent needs to be aware of the largest eigenvalue of Laplacian matrix L. However, employing the results in Ref. [29], we have λL < 2dimax ≤ 2(N − 1). Then, we can renew the event condition (6) as follows:

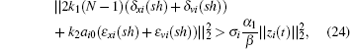
where α1 = 3h + 1 + 3/2a2 − (3h + 4)/2a − (h2 + h − 3h3)(2k1 (N − 1) + k2). Based on the same constraints in Eq. (15), it is obvious that α1 < α. So the multi-agent systems (1) with the virtual leader (2) utilizing the event condition (24) can also reach consensus tracking.

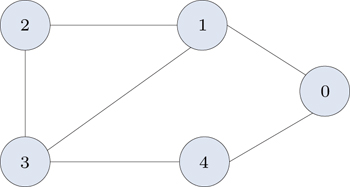
4. Simulations

In this section, numerical simulations are presented to demonstrate the effectiveness of the proposed event-based control strategy. Here we consider second-order multi-agent systems with four agents and one virtual leader, whose dynamics are described by Eqs. (1) and (2). The corresponding communication topology is shown in Fig. 1.

Fig. 1. Network topology composed of four agents and one virtual leader.

Without loss of generality, the weights of all the edges are assumed to be 1. Thus, we can obtain 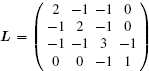, B = diag{1,0,0,1}. By Setting k1 = k2 = 1, the matrix M is given by 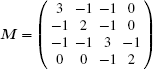. It is easy to obtain that λL = 4 and λM = 4.2631. According to the conditions given by Eq. (15), we choose the sampling period h = 0.002 and a = 5, resulting in α ≈ 0.657 and β = 1.315. Assume that σ1 = σ2 = 0.6, σ3 = 0.8, and σ4 = 0.99. Without loss of generality, we choose x0(t) = 0.3 + 0.5t, x(0) = [4.7− 3.3 0.5− 6.3]T, and υ(0) = [−11.5 − 0.7 2]T.

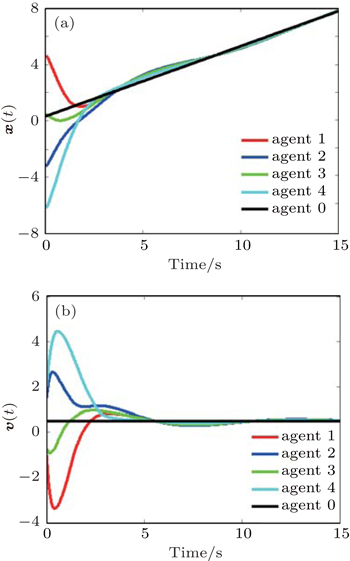
Figure 2 shows that the position states and the velocity states of all agents can converge to those of the virtual leader; in a sense, that second-order multi-agent systems (1) with the virtual leader (2) applying the protocol (3) with the condition (6) can ultimately achieve consensus tracking. Here, we also provide the corresponding triggered instants of each agent in Fig. 3.

Fig. 2. The (a) positions and (b) velocities of systems (1)–(2) using protocol (3).
Fig. 3. Triggered instants of systems (1)-(2) applying event condition (6).
5. Conclusion

In this paper, we have investigated event-triggered consensus tracking of second-order multi-agent systems. Utilizing the Lyapunov function method, we have obtained sufficient conditions to guarantee second-order multi-agent systems asymptotically achieve consensus tracking. A novel distributed event-triggered strategy has been proposed, in which continuous communication among agents can be avoided and energy consumption can be further reduced. However, it is noted that the sampling of each agent is assumed to be generated at the same moment. Besides, the acceleration of the virtual leader was assumed to be zero and the model considered in this paper does not contain some complicated cases such as measurement noises, switching topology and so on. Therefore, one of the future research directions is devoted to studying the event-triggered consensus tracking of heterogeneous multi-agent systems with asynchronous sampling, measurement noises and switching topology.

Reference
1Su H SWang X FLin Z L 2009 IEEE Trans. Autom. Control 54 293
2Yan JGuan X PLuo X Y 2011 Chin. Phys. 20 018901
3Yan JGuan X PLuo X Y 2011 Chin. Phys. 20 048901
4Hengster M KYou K YLewis F LXie L H 2013 Automatica 49 414
5Wu Z HPeng LXie L BWen J W 2013 Chin. Phys. 22 128901
6Zhang X JCui B TLou K 2014 Chin. Phys. 23 110205
7Wang NWu Z HPeng Li 2014 Chin. Phys. 23 108901
8Li LFang H J 2013 Chin. Phys. 22 110505
9Sun Y ZLi WRuan J 2013 Chin. Phys. 22 030510
10Sun F LZhu W 2013 Chin. Phys. 22 110204
11Gao L XYan H JJin D 2010 Chin. Phys. 19 050520
12Åström K JBernhardsson B2002Proc. IEEE Conf. Decision and ControlDecember, 2002Las Vegas, Nevada USA201110.1109/CDC.2002.1184824
13Demir OLunze J 2014 Inter. J. Control 87 169
14Mazo MTabuada P 2011 IEEE Trans Autom. Control 56 2456
15Guinaldo MDimarogonas D VJohansson K HSanchez JDormido S2011Proc. IEEE Conf. Decision and ControlDecember 12–15, 2011Orlando, USA255310.1007/978-3-319-21299-9-7
16Guo GDing LHan Q L 2014 Automatica 50 1489
17Xiao FMeng X YChen T W 2015 Inter. J. Control 88 391
18Dimarogonas D VFrazzoli EJohansson K H 2012 IEEE Trans. Autom. Control 57 1291
19Garcia ECao Y CYu HAntsaklisc PCasbeerb D 2013 Inter. J. Control 86 1479
20Seyboth G SDimarogonas D VJohansson K H 2013 Automatica 49 245
21Fan YFeng GWang YSong C 2013 Automatica 49 671
22Meng X YChen T W 2013 Automatica 49 2125
23Hu J PChen G RLi H X2011Kybernetika47630
24Hu J PChen G RLi H X2011Proc. Chin. Control Conf.July 22–24, 2011Yantai, China4819
25Xie D SYuan D MLu J WZhang Y J 2013 Trans. Inst. Meas. Control 35 426
26Li H QLiao X FHuang T WZhu W 2015 IEEE Trans. Autom. Control 60 1998
27Hong Y GHu J PGao L X 2006 Automatica 42 1177
28Horn R AJornson C R1985Matrix AnalysisNew YorkCambridge University
29Grone RMerris R 1994 SIAM Journal on Discrete Mathematics 7 221