Although there are various chiral materials in nature, the chirality-associated optical phenomena are usually very weak. Artificial chiral metamaterials have exhibited lots of optical properties in recent years,^[1–4] including plasmon-enhanced circular dichroism (CD) and optical activity, which exhibit potential applications in physics, biology, and chemistry.^[5–7] This is because artificial metamaterials associated with many novel optical properties^[8–12] can lead to strong couplings between electric and magnetic responses attributed to their peculiar geometric structures as well as their unit sizes much smaller than the wavelength of radiation.^[13–18] Utilizing these strong electromagnetic couplings in chiral geometric structures, the strong CD and optical activity can occur.^[19–26] Recently, Kuwata-Gonokami et al. have demonstrated that the giant optical activity could exist in two-dimensional gratings consisting of chiral gold nanostructures with subwavelength features.^[19] Decker et al. have shown that the obvious CD can be produced by a double-layer chiral planar magnetic metamaterial at near-infrared wavelengths.^[21] Kwon et al. obtained the strong CD and optical activity through adopting a genetic algorithm in a similar bistratal planar chiral metamaterial in the near-infrared regime.^[22] Cao et al. realized an obvious CD and optical activity through a chiral metamaterial which is integrated with Ge₂Sb₂Te₅ phase-change material in the mid-infrared regime.^[24] Gansel et al. investigated the three-dimensional (3D)-chiral gold helix which can be used as a broadband circular polarizer.^[27] However, to obtain the optimum CD through adjusting the structure of chiral metamaterial is limited to the sign and magnitude of the CD rather than the frequency response. Plum et al. have investigated that the optical activity can be excited in an extrinsically chiral metamaterial.^[28,29] Singh et al. have shown that the sign and magnitude of CD can be tuned by the asymmetric factor of the metamaterial at normal incidence, but these were produced by planar achiral metamaterials.^[30]

In this work, we investigated the optimum CD in a chiral metamaterial composed of a 3D-extrinsically-chiral unit cell. This unit cell has a dual-chiral characteristic, which means that both the entire configuration and the component structures are chiral. By adjusting the asymmetry of structure, we realized the further improved CD in the terahertz regime, which falls between the microwaves and far-infrared domain and has unique application potentials. Since the discovery of terahertz proposed by Fleming in 1974, the research of terahertz has made great progress. It has various potential applications in technological domains, such as security detection, sensing, biomedical imaging, and molecular recognition.^[31–33] Currently, there are few papers about improving CD in THz region. In particular, the large CD in THz is very useful for the molecular recognition, highly efficient terahertz polarization rotators, and vibration sensor.^[30] Consequently, the development of metamaterials with large CD in THz region is very important.

Let us first consider the theoretical analysis of the electromagnetic propagation through a certain slab of uniform chiral medium when a plane wave comes in along the +z direction, with the electric field , where ω, k, and I_j represent the frequency, wave vector, and amplitudes, respectively. The transmitted light is then given by . The Jones matrix T_lin, which relates the generally complex amplitudes of the incident field to that of the transmitted field, can be described as

In the case of a circular polarization, the T matrix connecting the incident and the transmitted circularly polarized components can be calculated from the linear transmission matrix by using the following basis transformation:

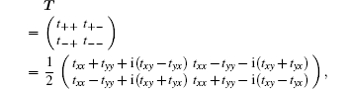
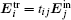
Circular dichroism is defined as CD = |A₊| − |A₋|, where the circular-polarization absorbances of RCP and LCP are A₊ and A₋, given by A₊ = 1 − |R₊| − |T₊| and A₋ = 1 − |R₋| − |T₋|, respectively. Meanwhile, R₊ and R₋ are the circular polarization reflections for RCP and LCP, respectively. In general, the reflections for RCP and LCP are identical through the metamaterials, and thus the circular dichroism is also defined as CD = |A₊| − |A₋| = |T₊| − |T₋|.

To investigate the transmission characteristics of the metamaterial, we have used full-wave numerical simulations by a commercial package based on the finite-element method (FEM).^[34] We consider the right-handed circularly polarized wave (RCP, +) and left-handed circularly polarized wave (LCP, −) to illuminate our proposed structures along the +z direction. Figure 1 schematically depicts the unit stereogram of our single-layer and bilayer chiral metamaterials. In this paper, aluminum is selected as the metallic material for the resonator on a silica substrate (ε = 2.1). The introduced chiral resonator consists of a square two-gap asymmetric split ring resonator (ASRR) with the geometric parameters as follows: The length of the side a = 60 μm, the shifted distance of the asymmetric gap d = 10 μm, aluminium width w = 6 μm, gap width g = 3 μm, and aluminium thickness is 0.2 μm. The in-plane unit size of the periodic metamaterial is 75 μm × 75 μm.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. The schematic of the chiral resonator that composes chiral metamaterials, with the unit cell shown on the right. The square two-gap asymmetric split ring resonator (ASRR) with geometric parameters as follows: a = 60 μm, d = 10 μm, w = 6 μm, g = 3 μm. (a) The single-layer chiral metamaterial. (b) The symmetric bilayer metamaterial (SBM). (c) The asymmetric bilayer metamaterial (ASBM).

Figure 1 is the diagram of the planar structures proposed in this work. Figure 1(a) exhibits a single-layer chiral metamaterial. Figure 1(b) exhibits a bilayer chiral metamaterial with dual chiral layers. That is, it is composed of the forward and backward ASRRs, where these two ASRRs are in mirror symmetry. We call this structure symmetric bilayer metamaterial (SBM) for convenience. Similar to that in Fig. 1(b), there is another bilayer metamaterial shown in Fig. 1(c). The difference is that for the latter the backward ASRR is rotated by 180 degrees, which is called asymmetric bilayer metamaterial (ASBM) for convenience. Both the SBM and ASBM are a kind of dual-chiral metamaterial.

The transmission spectra for different structures normally illuminated by circularly polarized terahertz waves are presented in Fig. 2. When the RCP and LCP waves propagate through the single-layer chiral metamaterial [Fig. 2(a)], the numerical results show that T₊₊ = T₋₋ and T₋₊ = T₊₋. Utilizing the equation CD = |T₊| − |T₋|, thus there is almost no CD phenomenon as shown in Fig. 2(d). However, when we use an SBM instead of the single-layer structure, it is interesting to find that T₊₊ ≠ T₋₋ but T₋₊ = T₊₋ at 0.87 THz and 1.16 THz in Fig. 2(b), it provides an opportunity for the realization of CD effect at the terahertz spectrum. Utilizing the equation CD = |T₊| − |T₋|, as well as T₋₊ = T₊₋ and T₊₊ ≠ T₋₋ in the dual-chiral metamaterials, it is obvious that the circular dichroism CD = |T₊₊| − |T₋₋|. Figure 2(c) shows that two CDs corresponding to these two frequencies are about 0.35 and 0.4, respectively. Similar to the SBM metamaterial, for the ASBM, figure 2(c) shows there are two resonances with T₊₊ ≠ T₋₋, while T₋₊ = T₊₋ at 1.00 THz and 1.20 THz. Intriguingly, the difference between T₊₊ and T₋₋ is obviously enlarged. The corresponding CDs are about 0.45 and 0.5 in Fig. 2(f), this result improves about 25%. Therefore, it indicates the implementation that the value of CD can be improved by changing the asymmetry of chiral ASRRs in both sides of the dual-chiral metamaterial.

Generally, for a linear light normally travelling through the medium, there is another characteristic for a chiral structure, that is, the rotation of the polarization angle θ. This is a useful effect conventionally known as optical activity. For the proposed dual-chiral metamaterials, the polarization rotation angle θ of the transmitted light is given by θ = (argt₊₊ − argt₋₋)/2, where t₊₊ and t₋₋ denote the complex transmitted coefficients of RCP and LCP, respectively, while arg represents the phase angle. The ellipticity of the transmitted wave that is connected to the power transmittance T₊ and T₋ by

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. The circular transmission spectra for (a) the single-layered chiral metamaterial, (b) the symmetric bilayer metamaterial (SBM), and (c) the asymmetric bilayer metamaterial (ASBM). Correspondingly, calculated circular dichroism is presented in panel (d) for the single-layered chiral metamaterial, in panel (e) for SBM, and in panel (f) for ASBM.

Fig. 3.

	Figure Option ViewDownloadNew Window
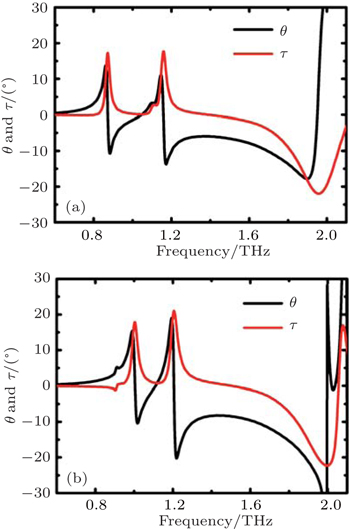	Fig. 3. The polarization angle θ and the ellipticity of the transmitted wave. (a) The symmetric bilayer metamaterial (SBM). (b) The asymmetric bilayer metamaterial (ASBM).

In the above text, we have obtained the improvement of CD through the rotation operation from SBM to ASBM. We consider changing the value of the parameter d of the ASBM. As illustrated in Figs. 4(a)–4(f), there are different CD results through adjusting the values of d in the ASBM. This starts from achiral metamaterial (d = 0 μm), where no CD phenomenon appears [Fig. 4(a)]. Once it turns into the dual-chiral structure (d ≠ 0), two distinct CD phenomena (CD1 and CD2) emerge. Moreover, these two CDs can be tuned with the increase of d [Figs. 4(b)–4(f)]. From Fig. 4(g), it can be clearly observed that these two CDs are gradually enhanced with d increasing, and reach the maximum, about 0.5 and 0.55 at d = 15 μm. Therefore, it is verified that the CDs in our dual-chiral metamaterial can be further improved through operating the asymmetry (d ≠ 0) in the ASBM.

We also studied the forward and backward surface current distributions at the frequencies where CD happens for the ASBM (d = 15 μm) in Fig. 5. The inherent magnetic–dipole and electric–dipole exist respectively due to the fact that the forward and backward structures are both ASRRs. In Fig. 5(a), the forward current distribution of ASBM at 0.840 THz forms a closed loop which looks like the subradiant magnetic–dipole, and the direction of the backward current loop is the same as the forward. The entire current distribution leads to the electric-dipole-like characteristic and the value of the CD (−0.05) closes to 0. At the frequency of CD1, the currents are both excited only in the left wire arm in forward and backward ASRR [Fig. 5(b)], which form a dipole and give rise to the resonance at 0.987 THz. Thus, a dual-magnetic-dipole is excited in the dual-chiral metamaterial by the opposite directions between these two currents,^[21,35] thus a stronger CD1 (0.5) happens. Figure 5(c) reveals that the right wire arms of forward and backward ASRRs are excited with currents characterized by a stronger field confinement at 1.308 THz. Another stronger CD2 (0.55) is caused by the dual-magnetic-dipole which is formed by the opposite current directions in the forward and backward ASRRs. At 1.938 THz, there are two symmetric current loops at the left and right arms that are parallel to each other in the forward and backward ASRR [Fig. 5(d)], which are like an electric dipole with highly radiative and low-quality-factor natures, corresponding to the weak CD. This result is similar to that in Ref. [36], where large CD could be obtained through enhancing the local resonant current. As long as the coupling between the forward and the backward layers is strong, the large CD will be obtained, like the gammadions in Ref. [21] and crossed-gratings in Ref. [35]. For our proposed bilayer metamaterial, a magnetic dipole is formed in the bilayer metamaterial when the currents of the forward and backward layers are opposite to each other. Consequently, the large CD is a result of the local currents forming a stronger dual-magnetic-dipole in the dual-chiral structures.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. (a)–(f) The circular dichroism with a variation of the asymmetric distance d. (g) The variation trend of CD1 and CD2 with d increasing.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. The currents distribution of forward and backward in ASBM at different frequencies: (a) 0.840 THz, (b) CD1, (c) CD2, (d) 1.938 THz.

In summary, we obtained a large CD effect in the THz region through a dual-chiral metamaterial based on two chiral asymmetric split ring resonators excited by normally incident light. It is found that the CD can be improved by adjusting the asymmetry between the two ASRRs in the terahertz regime. In addition, the underlying mechanism for the enhanced CD is discussed in terms of the induced dual magnetic-dipole response, attributed to the strong coupling between the forward and backward resonant structures of the bilayer geometry. This significant CD effect in the proposed dual-chiral metamaterial is very useful for sensing, biomedical imaging, and molecular recognition.