Cite this Article
Zhu Xu-Hui, Chen Xiang-Rong, Liu Bang-Gui. First-principles investigation of electronic structure, effective carrier masses, and optical properties of ferromagnetic semiconductor CdCr2S4. Chinese Physics B, 2016, 25(5): 057501  
Permissions
First-principles investigation of electronic structure, effective carrier masses, and optical properties of ferromagnetic semiconductor CdCr2S4
Zhu Xu-Hui1, 2, Chen Xiang-Rong1, 3, †, , Liu Bang-Gui2, ‡,
Institute of Atomic and Molecular Physics, College of Physical Science and Technology, Sichuan University, Chengdu 610065, China
Beijing National Laboratory for Condensed Matter Physics, Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China
Key Laboratory of High Energy Density Physics and Technology of Ministry of Education, Sichuan University, Chengdu 610064, China

 

† Corresponding author. E-mail: xrchen@scu.edu.cn

‡ Corresponding author. E-mail: bgliu@iphy.ac.cn

Project supported by the Joint Fund of the National Natural Science Foundation of China and the China Academy of Engineering Physics (Grant Nos. U1430117 and U1230201).

Abstract
Abstract

The electronic structures, the effective masses, and optical properties of spinel CdCr2S4 are studied by using the full-potential linearized augmented planewave method and a modified Becke–Johnson exchange functional within the density-functional theory. Most importantly, the effects of the spin–orbit coupling (SOC) on the electronic structures and carrier effective masses are investigated. The calculated band structure shows a direct band gap. The electronic effective mass and the hole effective mass are analytically determined by reproducing the calculated band structures near the BZ center. SOC substantially changes the valence band top and the hole effective masses. In addition, we calculated the corresponding optical properties of the spinel structure CdCr2S4. These should be useful to deeply understand spinel CdCr2S4 as a ferromagnetic semiconductor for possible semiconductor spintronic applications.

PACS: 75.50.Pp;71.18.+y;78.20.Ci;71.15.Mb;
Keyword:CdCr2S4 semiconductor;effective mass;optical properties;density functional theory;
1. Introduction

Recently, the ferromagnetic semiconductive spinel compounds have been studied for potential candidates for semiconductor spintronic devices.[1–5] A great deal of experimental attention has been concentrated on the cubic spinel compound CdCr2S4. In 2005, Hemberger et al.[1] reported that the cubic spinel CdCr2S4 has relaxor-like dielectric properties and colossal magnetocapacitance. Sun et al.[6] observed several interesting behaviors in spinel system CdCr2S4, showing that a glassy dipolar state occurs near TC ∼ 85 K and a ferroelectric ordering occurs near Tp ∼ 56 K. Gnezdilov et al.[7] showed pronounced phonon anomalies indicating a symmetry reduction and Cr off-centering in the cubic unit cell of CdCr2S4. Subsequently, Oliveira et al.[8] demonstrated that a linear coupling between the magnetic and polar order parameters is sufficient to justify the appearance of a magnetic cluster in the paramagnetic phase of CdCr2S4. Furthermore, using muon spin rotation/relaxation spectroscopy (μSR), Hartmann et al.[9] studied the magnetic properties of CdCr2S4.

On the theoretical side, with an ab initio method, Shanthi et al.[10] calculated the electronic structures for both the nonmagnetic and the ferromagnetic states of CdCr2S4, and presented that CdCr2S4 corresponds to a ferromagnetic semimetallic ground state, with very low density of states at the Fermi energy and a nearly gapped structure. Fennie et al.[11] studied the dielectric properties, zone-center phonons and Born effective charges of the ferromagnetic spinel CdCr2S4. In the same year, Lunkenheimer et al.[12] provided strong evidence that the variation of the dielectric constant at the magnetic transition and the colossal MC effect in this material are caused by a speeding up of relaxation dynamics under the formation of the magnetic order. In 2008, within the local spin-density approximation LSDA and LSDA+U, Yaresko[13] obtained the semiconductive electronic band structure and exchange coupling constants in CdCr2S4 spinels. Recently, using a modified Becke–Johnson (mBJ) exchange plus local density approximation correlation, Guo et al.[14] obtained accurate energy gaps and optical properties of ferromagnetic semiconductors CdCr2S4. However, more theoretical investigation is needed for achieving more insights of the ferromagnetic semiconductor spinel material.

Here, we use the full-potential density-functional-theory method to investigate the electronic structures, effective carrier masses, and optical functions of the CdCr2S4, with the spin–orbit coupling taken into account and the semiconductor gap accurately calculated. This paper is organized as follows. The theoretical methods and computational details are given in Section 2. Our calculated results and some discussions are presented in Section 3. Finally, a summary of our main results is given in Section 4.

2. Theoretical methods

The electronic structures of ferromagnetic semiconductor CdCr2S4 in spinel structure were carried out by using a full potential linearized augmented plane waves (FPLAPW) method in the framework of the DFT[15,16] as implemented in the Wien2k package.[17,18] We use a modified Becke–Johnson (mBJ) semi-local exchange potential[19] plus the local density approximation (LDA) for the correlation potential[20,21] to do our main DFT calculations, and additionally do some calculations with the popular generalized gradient approximation (GGA)[22] for necessary comparison. It is well known that the mBJ exchange plus LDA correlation can produce accurate semiconductor gaps for semiconductors and insulators[14,20,23–26] and overcome the usual LDA and GGA underestimation of the band gaps. The full relativistic effects are calculated with the Dirac equations for core states, and the scalar relativistic approximation is used for valence states.[27–29] The spin–orbit coupling (SOC) is taken into account. The maximum l quantum number for the wave function expansion inside atomic spheres was set to lmax = 10. The convergence parameter Rmt × Kmax is set to 8 and the radii Rmt of the atomic spheres are chosen as 2.47 (Cd), 2.43 (Cr), and 2.05 (S) Bohr for CdCr2S4. We use 1000 k-points in the first Brillouin zone for self-consistent calculation and 10000 k-points for optical properties calculation. The self-consistent calculations are considered to be converged only when the integration of the absolute charge-density difference between the input and output electron density is less than 0.0001|e| per formula unit, where e is the electron charge.

3. Result and discussion
3.1. Crystal structure

CdCr2S4 is a typical ferromagnetic semiconductor with the spinel structure AB2X4, which belongs to the space group 227 (Fd-3m). The primitive cell crystal structure is shown schematically in Fig. 1. The atomic sites with symmetries are Cd (8a, Td), Cr (16d, D3d), S (32e, C3v)[30] in the cubic spinel structure. At first, the CdCr2S4 is optimized from the experimental lattice constant 10.240 Å[31] with the popular GGA. The optimized lattice constant, with the available experimental data[31] and the theoretical results,[14,32] is presented in Table 1. The final optimized value 10.298 Å is 0.57% larger than the experimental one.[31] The SOC effect makes the calculated total energy become lower. Because the easy magnetization axis of the ferromagnetic spinel CdCr2S4 lies along the [100] crystallographic axis,[33] we consider only the [001] magnetization direction in the spin–orbit coupling calculation.

Fig. 1. The primitive cell structure of spinel CdCr2S4.
Table 1.

The lattice constants (a), primitive cell volume (V), semiconductor energy gap (Eg) and the magnetic moment (M) in the spinel ferromagnetic semiconductor CdCr2S4.

.
3.2. Electronic properties

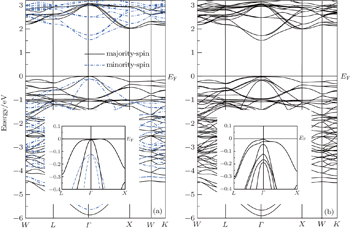
To overcome LDA and GGA underestimation of energy gaps, we have used the mBJ approximation. The electronic band structures for the spinel structure CdCr2S4 along the high symmetry directions in the first Brillouin zone are calculated. The effect of the spin–orbit coupling is investigated. In Fig. 2, we present the spin-polarized band structures of CdCr2S4 calculated with mBJ [Fig. 2(a)] and mBJ plus SOC [Fig. 2(b)]. It is clear that the bottom of the conduction bands and the top of the valence bands are situated at the Γ symmetry point, showing direct band nature for CdCr2S4, which is consistent with the result of Guo et al.[14] The semiconductor energy gap calculated with mBJ+SOC is 1.52 eV, a little lower than the theoretical value 1.67 eV calculated with mBJ only.[14] The energy gap calculated with mBJ [Fig. 2(a)] is significantly larger than the previous DFT results: 0.82 eV with GGA,[14] 0.77 eV with LSDA,[11] and 1.47 eV with LSDA+U.[11] It is clear that the mBJ potential can provide a better band gap than other theoretical methods in comparison with the experimental 1.8 eV.[32] In addition, the calculated Fermi energy becomes higher by 0.018 eV after SOC is taken into account. Comparing Fig. 2(a) with Fig. 2(b), we can see that the SOC effect has little influence on the conduction band bottom. In order to explain more clearly the SOC effect on the valence band maximum, we present the insert figures which show the energy band near the Fermi surface in Fig. 2. It is interesting that the degeneracy of the six bands at the Γ point is completely lifted by the SOC effect, as shown in Fig. 2(b). For both of the majority-spin and minority-spin channels, the valence bands corresponding to Γ15 states at the Γ point divide into three energy levels.

Fig. 2. Energy bands of CdCr2S4 calculated with mBJ (a) and with mBJ-SOC (b).

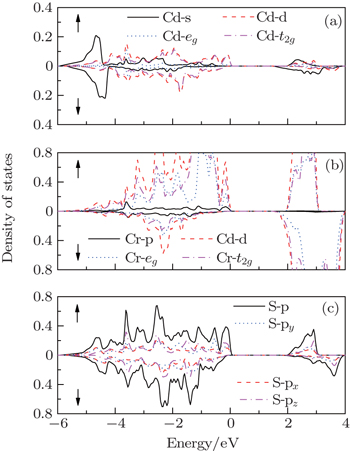
Furthermore, we have calculated the total density of states (TDOS) of CdCr2S4 between −6 eV and 4 eV with both mBJ and mBJ plus SOC, and present the results in Figs. 3(a) and 3(b). The amplified density of states in Figs. 3(c) and 3(d) further shows the effect of SOC. These figures are consistent with the band structures in Fig. 2. In addition, the partial densities of states (PDOS) have been calculated with mBJ plus SOC and are presented in Fig. 4. They are important to understand the contribution of every atom and specific electronic states of CdCr2S4 to the valence band and conduction band near the Fermi surface. The study shows that the states in the conduction band bottom are mainly derived from both the Cr d states and the Cd s state, but the lowest state in the conduction band bottom is the Cd s state. As for the valence band top, the S p states play a dominant role, but the Cr d(t2g) states also make a substantial contribution. These results are also consistent with the band structures.

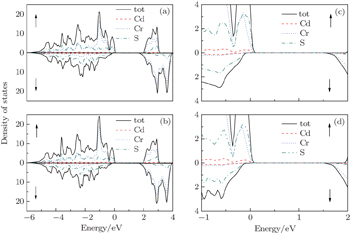Fig. 3. The spin-resolved total density of states ((a) mBJ, (b) mBJ-SOC) and the amplified parts near the Fermi energy ((c) mBJ, (d) mBJ-SOC) of CdCr2S4.
Fig. 4. The spin-resolved partial density of states of CdCr2S4 with mBJ-SOC: (a) Cd s and Cd d electrons; (b) Cr p and Cr d electrons; (c) S p electrons.
3.3. Effective carrier masses

The electronic structures of a semiconductor near the band valence top and the conduction band bottom are vital to its electronic transport properties. The effective mass theory will undoubtedly become one of the direct ways to understand the material properties. If the band extremum is located in the center of the Brillouin zone, the band dispersion function E(p) should be parabolic for a small p value. Using effective mass approximation theory, the dispersion relation near the conduction band minimum (CBM) can be written as

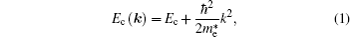
where is the electron effective mass. The effective mass of electrons of the CdCr2S4 semiconductor can be calculated from the band structure near the conduction band minimum. The diagonal elements of the effective mass tensor for the electrons near the conduction band bottom are calculated using the following relation:[34]

Therefore, the effective mass of the electron is evaluated by fitting the electronic band structure near the bottom to a parabolic function. The hole effective masses can be calculated in a similar way. As usual, we have three holes in each of the spin channels.

Without the spin–orbit coupling, we use 1000 points along three main high-symmetry directions: [001], [110], and [111] in the first Brillouin zone, then fit the 0.5% range of the dispersion curves near the CBM and VBM by using Eq. (2). There are two heavy holes and one light hole corresponding to the top of the valence bands for both the majority-spin and minority-spin states. They correspond to the doublet and singlet. By fitting the function, we get the electron effective mass and the hole effective mass along the three directions near the Γ point. The results are presented in Tables 2 and 3, respectively. The electronic effective masses along the three directions are almost the same, which means that the electron effective mass is isotropic in the k space. It can be seen in Table 3 that along the [001] direction, the heavy-hole and light-hole effective mass are 0.289 and 0.222 of the majority-spin channel, much larger than 0.123 and 0.102 of the minority-spin channel. The same trend is also true for the other two high-symmetry directions [110] and [111]. For the majority-spin channel, without the spin–orbit coupling, the hole effective mass along the three directions has the relationship: and . Unlike the electron effective mass, the hole effective mass is anisotropic in the k space.

Table 2.

The electron effective masses along [001], [110], and [111] directions of CdCr2S4 calculated by mBJ and mBJ-SOC.

.
Table 3.

The hole effective masses and along [001], [110], and [111] directions of CdCr2S4 calculated with both mBJ and mBJ-SOC.

.

The spin–orbit coupling changes substantially the band structures. There appears a spin–orbit splitting band near VBM. We also choose 1000 points along the three high-symmetry directions, [001], [110], and [111], in the first Brillouin zone, and fit the 0.5% range of the dispersion relation near the CBM and VBM. The final fitting results are presented in Tables 2 and 3. Observing the data in Table 2, the calculated electron effective mass is equally 0.094 along the high-symmetry directions-[001]. As for the other high-symmetry directions, the electron effective mass is 0.096, 0.002 larger than that along the directions-[110] with the mBJ method. In addition, the electron effective mass is 0.004 smaller than the value 0.093 calculated along the directions-[111] with the mBJ method. We can conclude that the electron effective mass is almost isotropic in the k space. We found that the hole effective masses in Table 3 are very different from those calculated with mBJ only. This is because the spin–orbit coupling causes interaction between the minority-spin states and the majority-spin states. For each of the spin channels, the degenerate states of the valence band top are divided into the heavy hole band, light hole band, and the spin–orbit split band in series from the Fermi energy. The upper three valence bands are originated mainly from the majority-spin channel, and the lower three mainly from the minority-spin channel. The hole effective mass and the effective mass of spin–orbit split band along the three directions for majority-spin are larger than those for minority-spin, respectively. For majority-spin, the hole effective mass along the three directions has the relationship: , , and . As the band structures show, the heavy hole in the majority-spin channel is very anisotropic near the center of the Brillouin zone, and in contrast, the other holes are substantially less anisotropic. In addition, the spin–orbit coupling makes the heavy holes much more heavy and the light holes lighter, and on the other hand it enhances the anisotropy of the heavy holes.

3.4. Optical properties

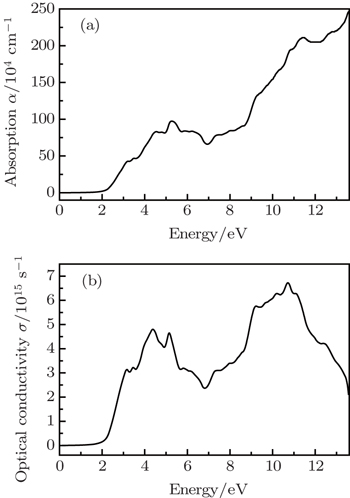
Ambrosch-Draxl et al.[35] have pointed out that the random phase approximation (RPA) is a useful method to calculate the screening and optical response in solids. They have provided formalism for treating optical properties within the RPA and implemented it with the Wien2k package.[17,18] Werner et al.[36] have successfully calculated the optical constants for 17 elemental metals with this method. The complex dielectric function of a solid is given as ε(ω) = ε1(ω) + iε2(ω) to describe the optical response of the material at photon energy ω. The imaginary part, ε2(ω), includes contributions from both of the spin channels. The real part, ε1(ω), can be extracted from the imaginary part using the Kramers–Kronig relation. The other optical coefficients can be expressed in terms of the dielectric function. Using the definition of direct transition and Kramers–Kronig relation,[37] we calculated optical properties of CdCr2S4 in the spinel cubic phase with mBJ calculation. Our calculated real and imaginary parts of the dielectric functions ε for CdCr2S4 are consistent with the result in the previous work.[14] The other optical properties are also studied. We present the optical absorption coefficient α(ω) and optical conductivity σ(ω) as functions of the photon energy in Fig. 5. For the absorption coefficient α(ω) in Fig. 5(a), the absorption edge starts from about 1.7 eV, corresponding to the Γ−Γ direct transition, and increases as the photon energy increases. The optical conductivity σ(ω) shown in Fig. 5(b) starts from 2.02 eV and then increases abruptly. These reflect the semiconductor gap because the electrons do not have enough energy to cross the energy gap to reach the conduction bands.

Fig. 5. The optical absorption coefficient α(ω) (a) and conductivity σ(ω) (b) as a function of photon energy for CdCr2S4.
4. Conclusions

In summary, the electronic structures and effective mass of ferromagnetic semiconductor CdCr2S4 have been investigated by using the full-potential linearized augmented plane wave (FP-LAPW) method within the density-functional theory. We use the modified Becke–Johnson (mBJ) exchange functional to accurately describe the electronic structures, especially the semiconductor gap, of ferromagnetic semiconductor CdCr2S4 and investigate the effects of the spin–orbit coupling. The calculated band structure shows a direct band gap, which accords well with the previous theoretical results and the experimental findings. The contribution of different bands was analyzed from the total and the partial density of states curves. The electronic effective mass and the hole effective masses are analytically determined by reproducing the calculated band structures near the Brillouin zone center on the basis of the effective-mass Hamiltonian. In addition, the important optical properties are investigated. These should be useful to study carrier transport properties of ferromagnetic semiconductor CdCr2S4 and similar magnetic semiconductors.

Reference
1Hemberger JLunkenheimer PFichtl RKrug von Nidda H ATsurkan VLoidl A 2005 Nature 434 364
2Lunkenheimer PFichtl RHemberger JTsurkan VLoidl A 2005 Phys. Rev. 72 060103
3Sun C PHuang C LLin C CHer J LHo C JLin J YBerger HYang H D 2010 Appl. Phys. Lett. 96 122109
4Xie Y MYang Z RLi LYin L HHu X BHuang Y LJian H BSong W HSun Y PZhou S QZhang Y H 2012 J. Appl. Phys. 112 123912
5Xie Y MYang Z RZhang Z TYin L HChen X LSong W HSun Y PZhou S QTong WZhang Y H 2013 Europhys. Lett. 104 17005
6Sun C PLin C CHer J LHo C JTaran SBerger HChaudhuri B KYang H D 2009 Phys. Rev. 79 214116
7Gnezdilov VLemmens PPashkevich Yu GPayen ChChoi K YHemberger JLoidl ATsurkan V 2011 Phys. Rev. 84 045106
8Oliveira G N PPereira A MLopes A M LAmaral J Sdos Santos M ARen YMendonc T MSousa C TAmaral V SCorreia J GAraujó J P 2012 Phys. Rev. 86 224418
9Hartmann OKalvius G MWappling RGunther ATsurkan VKrimmel ALoidl A 2013 Eur. Phys. J. 86 148
10Shanthi NMahadevan PSarma1 D D 2000 J. Solid State Chem. 155 198
11Fennie C JRabe K M 2005 Phys. Rev. 72 214123
12Lunkenheimer PFichtl RHemberger JTsurkan VLoidl A 2005 Phys. Rev. 72 060103
13Yaresko A N 2008 Phys. Rev. 77 115106
14Guo S DLiu B G 2012 J. Magn. Magn. Mater. 324 2410
15HohenbergKohn W 1964 Phys. Rev. 136 864
16Kohn WSham L J 1965 Phys. Rev. 140 1133
17Blaha PSchwarz KLuitz J 1990 Comput. Phys. Commun. 59 399
18Blaha PSchwarz KMadsen G K HKvasnicka DLuitz J2001WIEN2k, An Augmented Plane Wave + Local Orbitals Program for Calculating Crystal Properties3-9501031-1-2Universitat WienAustria
19Becke A DJohnson E R 2006 J. Chem. Phys. 124 221101
20Tran FBlaha P 2009 Phys. Rev. Lett. 102 226401
21Perdew J PWang Y 1992 Phys. Rev. 45 13244
22Perdew J PBurke KErnzerhof M 1996 Phys. Rev. Lett. 77 3865
23Singh D J 2010 Phys. Rev. 82 205102
24Singh D J 2010 Phys. Rev. 82 155145
25Singh D JSeo S S ALee H N 2010 Phys. Rev. 82 180103
26Kim Y SMarsman MKresse GTran FBlaha P 2010 Phys. Rev. 82 205212
27MacDonald A HPickett W EKoelling D D 1980 J. Phys. 13 2675
28Singh D J1994Planewaves, Pseudopotentials and the LAPW MethodBostonKluwer Academic Publishers
29Kunes JNovak PSchmid RBlaha PSchwarz K 2001 Phys. Rev. 64 153102
30Bruesch PDambrogi P 1972 Phys. Stat. Sol. (b) 50 513
31Slebarski AKonopka DKonopka D 1974 Phys. Lett. 50 333
32Sato K2001Crystal Growth and Characterization of Magnetic Semiconductors, in: Advances in Crystal Growth ResearchSato KFurukawa YNakajima KAmsterdamElsevier303309303–9
33Ehlers DTsurkan VKrug von Nidda H ALoidl A 2012 Phys. Rev. 86 174423
34Reshak A HAlahmed Z AAzam S2014Int. J. Electrochem. Sci.9975
35Ambrosch-Draxl CSofo J O 2006 Comput. Phys. Commun. 175 1
36Werner W S MGlantschnig KAmbrosch-Draxl C 2009 J. Phys. Chem. Ref. Data 38 1013
37Gaponenko S V1998Optical Properties of Semiconductor NanocrystalsCambridgeCambridge University Press