Cite this Article
Zhang Xiao-Lin, Wu Yuan-Yuan, Shao Xiao-Hong, Lu Yong, Zhang Ping. First-principles study of the elastic and thermodynamic properties of thorium hydrides at high pressure. Chinese Physics B, 2016, 25(5): 057102  
Permissions
First-principles study of the elastic and thermodynamic properties of thorium hydrides at high pressure
Zhang Xiao-Lin1, Wu Yuan-Yuan1, Shao Xiao-Hong1, †, , Lu Yong2, Zhang Ping2, ‡,
Beijing University of Chemical Technology, College of Science, Beijing 100029, China
Institute of Applied Physics and Computational Mathematics, Beijing 100088, China

 

† Corresponding author. E-mail: shaoxh@mail.buct.edu.cn

‡ Corresponding author. E-mail: zhang ping@iapcm.ac.cn

Project supported by the Long-Term Subsidy Mechanism from the Ministry of Finance and the Ministry of Education of China.

Abstract
Abstract

The high pressure behaviors of Th4H15 and ThH2 are investigated by using the first-principles calculations based on the density functional theory (DFT). From the energy–volume relations, the bct phase of ThH2 is more stable than the fcc phase at ambient conditions. At high pressure, the bct ThH2 and bcc Th4H15 phases are more brittle than they are at ambient pressure from the calculated elastic constants and the Poisson ratio. The thermodynamic stability of the bct phase ThH2 is determined from the calculated phonon dispersion. In the pressure domain of interest, the phonon dispersions of bcc Th4H15 and bct ThH2 are positive, indicating the dynamical stability of these two phases, while the fcc ThH2 is unstable. The thermodynamic properties including the lattice vibration energy, entropy, and specific heat are predicted for these stable phases. The vibrational free energy decreases with the increase of the temperature, and the entropy and the heat capacity are proportional to the temperature and inversely proportional to the pressure. As the pressure increases, the resistance to the external pressure is strengthened for Th4H15 and ThH2.

PACS: 71.15.Mb;62.20.–x;63.20.–e;
Keyword:first-principles calculations;thermodynamic properties;phonon spectra;thorium hydrides;
1. Introduction

Thorium and its hydrides are promising materials for advanced nuclear reactors with a high level of safety[1–8] and have attracted much attention. This is mainly due to their strength and stability at elevated temperatures while maintaining the desirable properties for neutron moderation.[9] In general, thorium hydrides crystalize in ThH2 and Th4H15 phases, which are both metallic solids.[2] Under ambient conditions, the stable thorium dihydride crystallizes in a body-centered tetragonal (bct) ionic structure with space group I4/mmm (No. 139). There also exists a face-centered cubic (fcc) fluorite-type structure with space group Fm-3m (No. 225), which is considered as a metastable phase of ThH2. As for the Th4H15 phase, it crystallizes in a body-centered cubic (bcc) structure with space group I-43d (No. 220), which has been reported to have superconductivity with a transition temperature of 8 K.[10] In addition, due to the large hydrogen-to-metal ratio, Th4H15 has been considered as a promising candidate for hydrogen storage.[11]

The structural and electronic properties and the optical phonon density of states of thorium hydrides at the ground state have been widely investigated in previous studies.[12–19] In order to support the experimental measurements or predict the microscopic physical properties that cannot be directly measured in the experiments, many theoretical studies were also performed for thorium hydrides. The optical phonon density of states of ThH2 was measured through inelastic neutron scattering,[14] and the bulk modulus of ThH2 was calculated by the linear muffin-tin orbital (LMTO) method.[15] The electronic properties of thorium hydrides were investigated by Shein et al.[16] through the full-potential LAPW (FLAPW) method. Moreover, the structural, elastic, and electronic properties of thorium hydrides at the ground state were studied by the first-principles calculations.[17] Despite abundant researches on thorium hydrides, relatively little is known regarding Th4H15. Until now, the elastic properties, phonon spectra, and thermodynamic properties are still unknown for Th4H15. Besides, there is still a lack of data about the elastic and thermal properties of thorium hydrides under high pressures, where a variety of interesting changes could show up. Furthermore, the stability of such competitive phases of thorium hydrides is also of interest for testing their practical applications.

In this paper, we perform a first-principles study on the elastic and thermodynamic properties of thorium hydrides at high pressures and make a systematic comparison with the corresponding behaviors at the ground state. The calculation method for the elastic constants and the computational details of first-principles are briefly introduced in Section 2. The calculation results are presented and discussed in Section 3. Finally, the conclusion is given in Section 4.

2. Computational details

The first-principles calculations were carried out by using the density-functional theory (DFT) as implemented in Vienna ab initio simulations package (VASP)[20] with the projector-augmented-wave (PAW) potential methods.[21] The electron exchange and correlation potential was evaluated by the generalized gradient approximation (GGA) introduced by Perdew, Burke, and Ernzerhof (PBE).[22] To ensure the calculation accuracy, the cutoff energy was set to 450 eV, and the self-consistent energy convergence of the calculation was set to 10−5 eV. The Brillouin zone (BZ) integration was performed by using 12 × 12 × 12k-points for ThH2 and 9 × 9 × 9 k-points for Th4H15 with the Monkhorst–Pack scheme.[23] The atomic structures were fully relaxed until the Hellmann–Feynman forces on all atoms were less than 1.0 × 10−5 eV/atom.

The elastic constants were calculated by means of a Taylor expansion of the total energy E(V,δ) based on the following law:[24–26]

where E(V0,0) and V0 are the total energy and the volume of the equilibrium cell with no strain, respectively, τi is an element in the stress tensor, ξi is a Voigt factor,[10] and Cij is the elastic constant. For cubic structures, fcc ThH2 and bcc Th4H15, there are three independent elastic constants (C11, C12, and C44). Thus, the elastic constants can be calculated with three different strains. The bulk modulus B and shear modulus G were obtained by the Voigt–Reuss–Hill (VRH) approximation,[27–29] i.e., and As for bct ThH2, the six independent elastic constants, C11, C12, C44, C13, C33, and C66, can be obtained with six different strains. The Young modulus E and Poisson’s ratio ν were obtained by the following formulas: E = 9BG/(3B + G) and ν = (3B − 2G)/[2(3B + 2G)]. The supercell approach and the small displacement method were used to calculate the phonon dispersions in the BZ and the corresponding phonon density of states (DOS) with the help of the PHONOPY code.[30] For the phonon calculations, the 2 × 2 × 2 supercells for bct and fcc phases containing 48 and 96 atoms were constructed, respectively. As for the bcc Th4H15, the 2 × 2 × 1 supercell containing 152 atoms was used. The quasi-harmonic approximation (QHA) method[31] was employed to calculate the thermodynamic properties associated with the phonon frequencies.

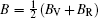
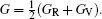
The Helmholtz free energy F (T,V) was calculated by

where E (V) is the ground state total energy at a given unit cell volume V, Fvib (T,V) is the vibrational energy of the lattice ions, and Fel (T,V) is the thermal electronic contribution to the free energy, which can be expressed by electronic entropy Sele (T,V) and energy due to the electron excitations Eele (T,V),

Under the quasi-harmonic approximation (QHA), Fvib (T,V) can be calculated by

where ω is the phonon frequency and g(ω) is the phonon density of states (DOS). The Sele (T,V) and Eele (T,V) can be calculated by

where n(ε,V) is the electronic density of states, f is the Fermi–Dirac distribution, and εF is the Fermi energy.

3. Results and discussion
3.1. Atomic structure

In the present study, we investigated three phases of thorium hydrides, i.e., bct ThH2, fcc ThH2, and bcc Th4H15(Fig. 1). At ambient conditions, thorium dihydride crystallizes in a bct ionic structure with space group I4/mmm. The Th and H atoms are located at the 2a (0, 0, 0) and 4d (0, 0.5, 0.25) sites (in Wyckoff notation), respectively (Fig. 1(a)). The relaxed lattice parameters a and c are 4.073 Å and 4.901 Å, respectively, which are in good agreement with the experimental values of 4.10 Å and 5.03 Å.[18] The fcc fluorite-type structure with space group Fm-3m is recognized as a metastable phase of ThH2 (Fig. 1(b)), whose structure can be obtained by modulating the base vectors of the bct phase. The optimized lattice parameter for fcc ThH2 is 5.487 Å, being in excellent agreement with the experimental value of 5.489 Å.[5] Besides, the energy–volume relationships of bct and fcc ThH2 were calculated to investigate the stability of ThH2 in energy, as displayed in Fig. 2. Obviously, at ambient pressure, the bct phase is more stable than the fcc phase. The obtained equilibrium volumes of the bct and fcc phases are 40.68 Å3 and 41.31 Å3, respectively, while the bcc Th4H15 phase has space group I-43d. In this structure, the Th atoms locate at the 16c (0.2087, 0.2087, 0.2087) site and the H atoms have two internal coordinates of 12a (0.375, 0, 0.25) and 48b (0.372, 0.219, 0.404) (Fig. 1(c)).[6] It is also found that the calculated equilibrium lattice parameter of bcc Th4H15 is 9.130 Å, being in agreement with the experimental value of 9.11 Å.[19]

Fig. 1. Crystal structures of (a) bct ThH2, (b) fcc ThH2, and (c) bcc Th4H15. The larger green balls are Th atoms and the smaller white ones are H atoms.
Fig. 2. Calculated ground-state energy vs. the primitive cell volume for ThH2 in bct and fcc phases.
3.2. Elastic constants at high pressures

Elastic constants are important mechanical parameters of solid materials, which determine the stiffness of a crystal against the external strain. Thus, we calculate the elastic constants to study the mechanical properties of thorium hydrides under different pressures. The calculated lattice parameters, elastic constants Cij, bulk modulus B, shear modulus G, Young’s modulus E, and Poisson’s ratio ν for bct ThH2, fcc ThH2, and bcc Th4H15 at different pressures are listed in Table 1. For the tetragonal structure, the structural stability criteria are C11 > 0, C33 > 0 C44 > 0, C66 > 0, (C11 − C12) > 0, (C11 + C33 − 2C13) > 0, and 2(C11 + C12) + C33 + 4C13 > 0. Obviously, the bct phase ThH2 is mechanically stable since its elastic constants satisfy the above mechanical stability criteria.[23]

Table 1.

Lattice parameter, elastic constants Cij, bulk modulus B, shear modulus G, Young’s modulus E, and Poisson’s ratio ν of bct ThH2 at different pressures.

.
Table 2.

Lattice parameter, elastic constants Cij, bulk modulus B of fcc ThH2 at different pressures.

.
Table 3.

Lattice parameter, elastic constants Cij, bulk modulus B, shear modulus G, Young’s modulus E, and Poisson’s ratio ν of bcc Th4H15 at different pressures.

.

As for the cubic structure, the structural stability criteria are C11 > 0, C44 > 0, C11 > |C12|, (C11 + 2C12) > 0. From the criteria, it is found that the bcc Th4H15 is mechanically stable, while the fcc ThH2 is unstable since C11 − C12 is negative. Nearly all the elastic constants increase with increasing pressure except C12 and C13 for the bct phase and C11 for the fcc phase (Fig. 3). After obtaining the elastic constants at different pressures, the polycrystalline bulk modulus B and Shear modulus G changing with pressure can be evaluated from the VRH approximation,[27–29] and the results are also shown in Fig. 3. It is found that both the bulk modulus and the shear modulus increase monotonically with pressure in the bct and bcc phases.

Fig. 3. Calculated elastic constants as a function of pressure for (a) bct ThH2, (b) fcc ThH2, and (c) bcc Th4H15.

The increasing rates of bulk moduli in these phases are slightly lower than those of shear moduli. It is well known that a high ratio of B/G is responsible for the ductility of polycrystalline materials. The critical value which separates ductile and brittle materials is around 1.75.[32] Our calculated B/G decreases from 3.29 to 1.37 for the bct phase with the pressure increasing from 0 to 60 GPa (Fig. 4(a)). The B/G ratio of bcc Th4H15 increases firstly from 1.76 to 1.82 with pressure increasing from 0 to 20 GPa, and then decreases to 1.60 with pressure further increasing to 60 GPa (Fig. 4(b)). At high pressures, the B/G ratios of bct and bcc phases are both lower than the critical value 1.75, indicating that thorium hydrides are of greater brittleness at high pressures. The Poisson ratio is defined as the absolute value of the ratio of transverse strain to longitudinal strain, which is used to quantify the stability of the crystal against shear. A larger Poisson ratio stands for a stronger plasticity. The Poisson ratios of thorium hydrides at different pressures are also listed in Table 1. It is noted that the Poisson ratios of bct ThH2 and bcc Th4H15 decrease with the increase of the pressure, indicating that the brittleness of thorium hydrides increases with pressure, in accordance with the above result from the B/G ratio.

Fig. 4. Dependencies of B/G ratio on pressure for (a) bct ThH2 and (b) bcc Th4H15.
3.3. Phonon dispersion and thermodynamic properties

In this work, the phonon dispersion was calculated based on the supercell approach and the finite difference method as implemented in the PHONOPY code. The calculated phonon dispersions for bct ThH2, fcc ThH2, and bcc Th4H15 are shown in Fig. 5. For all the phonon dispersions, an evident gap exists between the modes contributed by Th and H, which is attributed to that the Th atoms are much heavier than the H atoms. In these phonon dispersions, there are no imaginary frequencies for bct ThH2 and bcc Th4H15, which indicates that bct ThH2 and bcc Th4H15 can keep their mechanical stability up to at least 50 GPa. However, for fcc ThH2, there exist imaginary frequencies around the Γ point, resulting in that the fcc ThH2 is thermodynamically instable. The results are well consistent with our previous mechanical stability analysis for bct ThH2, fcc ThH2, and bcc Th4H15. Since thermodynamic properties play an important role in understanding the thermal response of a solid, it is necessary to know the thermal properties of thorium hydrides under high pressures and temperatures. The vibrational energy, entropy, and heat capacity were evaluated by the quasi-harmonic approximation in the temperature range from 0 to 1500 K (Fig. 6). As the pressure increases from ambient pressure to 50 GPa, the free energy is shifted upward. In contrast, the entropy and the heat capacity are proportional to the temperature and inversely proportional to the pressure. The entropy is maximum at ambient pressure. As is well known, the heat capacity can provide essential information about the vibrational properties of a crystal. As shown in Fig. 6(c), the heat capacity at constant volume (CV) increases exponentially with temperature when T < 600 K. With the temperature increasing towards 1500 K, the temperature dependence of the heat capacity becomes weaker and CV is governed by the atomic vibrations, approaching to the Dulong–Petit limit 3nR, where R is the gas constant. The trends of the heat capacity at ambient pressure and high pressure are similar. The specific heat at constant pressure CP can be obtained by using the relationship between CP and CV, i.e., where the constant volume thermal expansion αV is defined as In our calculations, the unit cell volumes assume a set of values. The calculated free energy versus volume for a number of selected temperatures is plotted in Fig. 7, from which the volume expansion with increasing temperature can be derived. As a result, the equilibrium volume V(T) and the bulk modulus B(T) can be obtained by fitting the data to the Vinet equation of states. Clearly, the bulk modulus B(T) decreases along with the increase of the temperature, as shown in Fig. 8. This temperature effect is very common for compounds and metals.[33,34] It is also found that the bulk modulus B(T) increases with pressure to a certain degree, and the resistance to the external pressure is strengthened. The calculated heat capacity CP of thorium hydrides are displayed in Fig. 9. As the pressure increases from 0 to 50 GPa, CP declines slightly.

Fig. 5. Calculated phonon dispersions (left panel) and phonon DOS (right panel) for (a) bct ThH2, (b) fcc ThH2, and (c) bcc Th4H15.
Fig. 6. Thermodynamic properties of (a) bct ThH2 and (b) bcc Th4H15 as a function of temperature under various pressures.
Fig. 7. Dependences of the Helmholtz free energy F(T,V) on crystal volume at various temperatures for (a) bct ThH2 and (b) bcc Th4H15.
Fig. 8. Temperature dependences of bulk modulus B(T) of (a) bct ThH2 and (b) bcc Th4H15.
Fig. 9. Specific heat capacities of (a) bct ThH2 and (b) bcc Th4H15.
4. Conclusion

The high pressure behaviors of Th4H15 and ThH2 have been studied by using the first-principles calculations based on the density functional theory. From the energy–volume relationship, the bct phase of ThH2 is more stable than the fcc phase at ambient pressure. At high pressures, the bct ThH2 and bcc Th4H15 phases are more brittle than they are at ambient pressure in terms of the calculated elastic constants and the Poisson ratio. The thermodynamic stability of these three phases has been discussed with the calculated phonon dispersion curves. In the pressure domain of interest, the phonon dispersions of bcc Th4H15 and bct ThH2 are positive, indicating that these two phases are stable, while the fcc ThH2 is unstable. The thermodynamic properties including the lattice vibration energy, entropy, and specific heat have been predicted based on the vibrational frequencies for the stable phases. Our results show that the vibrational free energy decreases with the increase of the temperature, while the entropy and the heat capacity are proportional to the temperature and inversely proportional to the pressure. It is found that the bulk modulus B increases with pressure, indicating the strengthened resistance to the external pressure for Th4H15 and ThH2. The calculated results in this study would be helpful for future experimental measurements on thorium hydrides.

Reference
1Keller C1976Berlin-Heidelberg-New York
2Zhao CGuo S PJiang HZhong G HSu Y H 2015 J. Phys. Chem. 119 13465
3Bickel MWedemeyer H1986Gmelin Handbook of Inorganic and Organometallic Chemistry, Thorium SupplementBerlinSpringer
4Benz RNaoumidis A1987Gmelin Handbook of Inorganic Chemistry: 8th Edition, Thorium SupplementBerlinSpringer
5Kleykamp H1992Gmelin Handbook of Inorganic and Organometallic Chemistry, Thorium SupplementBerlinSpringer10.1016/0022-3115(93)90282-4
6Brown DWedemayer H1993Gmelin Handbook of Inorganic and Organometallic Chemistry, Thorium SupplementBerlinSpringer10.1016/0022-328X(93)83431-T
7Nigel PGeckeis HHolloway J H1993Gmelin Handbook of Inorganic and Organometallic Chemistry, Thorium SupplementBerlinSpringer
8Shein I RIvanovskii A L 2008 J. Struc. Chem. 49 348
9Muller W MBlackledge J PLibowitz G G1968Metal Hydrides22
10Satterthwaite C BToepke I L 1970 Phys. Rev. Lett. 25 741
11Fisher E SRenken C J 1964 Phys. Rev. 135 A482
12Lau K FVaughan R WSatterthwaite C B 1977 Phys. Rev. 15 2449
13Weaver J HKnapp J AEastman D EPeterson D TSatterthwaite C B 1977 Phys. Rev. Lett. 39 639
14Dietrich MReichardt WRietschel H 1977 Solid State Commun. 21 603
15Brooks M SJohansson B 1985 Physica 130 516
16Shein I RShein K IMedvedeva N IIvanovskii A L 2007 Physica 389 296
17Wang B TZhang PSong H ZShi H LLi D FLi W D 2010 J. Nucl. Mater. 401 124
18Rundle R EShull C GWollan E O 1952 Acta Cryst. 5 22
19Zachariasen W H 1953 Acta Cryst. 6 395
20Kresse GFurthmuller J 1996 Phys. Rev. 54 11169
21Blochl P E 1994 Phys. Rev. 50 17953
22Perdew J PBurke KErnzerhof M1996Phys. Rev. B773865
23Monkhorst H JPack J D 1976 Phys. Rev. 13 5188
24Nye J F1957Physical Properties of CrystalsChapter VIII10.1107/S0365110X57002789
25Fan HWang S SLi Y H 2015 Acta Phys. Sin. 64 097101 (in Chinese)
26Liu Q JZhang N CLiu F SLiu Z T 2014 Chin. Phys. 23 047101
27Voigt W1928Lehrburch der KristallphysikTerubnerLeipzig
28Reuss AAngew Z 1929 Math. Mech. 9 49
29Hill R 1952 Phys. Soc. London 65 350
30Togo AOba FTanaka I 2008 Phys. Rev. 78 134106
31Yang X YLu YZheng F WZhang P 2015 Chin. Phys. 24 116301
32Pugh S F 1954 Philos. Mag. 45 823
33Wang B TZhang PLizarraga RMarco I DEriksson O 2013 Phys. Rev. 88 104107
34Souvatzis PEriksson 2008 Phys. Rev. 77 024110