Cite this Article
Liu Da-Ping. Topological phase boundary in a generalized Kitaev model. Chinese Physics B, 2016, 25(5): 057101  
Permissions
Topological phase boundary in a generalized Kitaev model
Liu Da-Ping†,
Department of Physics, Renmin University of China, Beijing 100872, China

 

† Corresponding author. E-mail: liudp@ruc.edu.cn

Project supported by the National Basic Research Program of China (Grant No. 2012CB921704).

Abstract
Abstract

We study the effects of the next-nearest-neighbor hopping and nearest-neighbor interactions on topological phases in a one-dimensional generalized Kitaev model. In the noninteracting case, we define a topological number and calculate exactly the phase diagram of the system. With addition of the next-nearest-neighbor hopping, the change of phase boundary between the topological and trivial regions can be described by an effective shift of the chemical potential. In the interacting case, we obtain the entanglement spectrum, the degeneracies of which correspond to the topological edge modes, by using the infinite time-evolving block decimation method. The results show that the interactions change the phase boundary as adding an effective chemical potential which can be explained by the change of the average number of particles.

PACS: 71.10.Pm;03.65.Vf;74.20.–z;
Keyword:topological superconductor;Majorana zero modes;entanglement spectrum;
1. Introduction

In recent years, the topological phase,[1–3] which cannot be described by Ginzburg–Landau symmetry breaking paradigm,[4,5] has been in the focus of research in condensed matter physics. Topological phases are usually characterized by the existence of an excitation gap in the bulk and the presence of gapless edge modes. The Kitaev chain,[6] a simple toy model of a one-dimensional (1D) topological superconductor[7–12] which contains a tight-binding chain of spinless electrons and a p-wave superconducting pairing term, is a typical example for the appearance of Majorana zero energy modes with strong Rashba spin–orbit interaction,[13–19] Recently, it has been reported that the Kitaev chain was realized in several nanowire experiments and the Majorana fermions (Majorana zero modes) were found in the nanowire systems.[20–25]

In this paper, we study a dimerization Kitaev chain[26] and focus especially on the effects of the next-nearest-neighbor (NNN) hopping and nearest-neighbor (NN) interactions on this system. In the non-interaction case, we first analyze the symmetry and the topological class[27–30] of the model in the Bogoliubov–de Gennes form.[31] Then we define a topological number and calculate the boundary between the topological and trivial phases. With exact diagonalization on a finite chain, we obtain the zero energy modes and the localization of the corresponding wave function.

In one-dimensional systems, topological phases can be characterized by the entanglement spectrum,[32–34] which can be obtained from the eigenvalues of a reduced density matrix. In the 1D topological superconductor, the degeneracy of the entanglement spectrum corresponds to the gapless edge modes.[33,34] On the matrix product state (MPS) formalism,[35–38] the entanglement spectrum can be calculated effectively by the infinite time-evolving block decimation (iTEBD) method.[39,40] For the dimerization Kitaev chain, we show the 2-fold degeneracy of the entanglement spectrum in the topological region. In the interaction case, we give a brief explanation on the relationship among the change of topological phase boundary, the effective chemical potential and the average particle number of the system.

The paper is organized as follows. In Section 2 we introduce the model and discuss the symmetries and the topological class of the model. To discuss the topological properties of the system, in Section 3 we define a winding number and obtain the phase diagram in the non-interacting case. In Section 4, we first calculate the zero energy modes of a finite chain and give their edge localization. Then we obtain the entanglement spectrum under open boundary conditions with and without interaction respectively. Finally, the results and conclusions are given in Section 5.

2. Model and symmetry

We first introduce a Kitaev/Majorana chain with the staggered NN and NNN hopping terms. Its Hamiltonian is given by

with

where the sums are taken over all the L cells, are the annihilation (creation) operators of the spinless fermion in cell vanishes on the open boundary conditions and on the periodic boundary conditions, A and B are sublattice indices for two points in a unit cell, t(1 + η) and t(1 − η) are staggered NN hopping amplitudes, Δ is the average superconducting pairing gap which is assumed to be real, tA and tB are the NNN hopping amplitudes, and μ is the chemical potential. The Hamiltonian (1) is reduced to the Kitaev model for tA = 0, tB = 0, and η = 0.

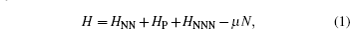
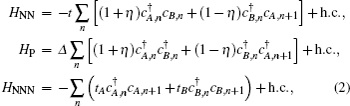
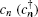
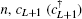
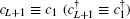
In order to analyze the topological properties of the system, we can first study the bulk band structure of the model and then calculate the boundary states of a finite chain. The Hamiltonian (1) can be expressed in the Bogoliubov–de Gennes form by a Fourier transformation

and

In momentum space, it reads

where and

with

where a is the lattice constant, and the first Brillouin zone is (−π/2a,π/2a] for two sites (each of which belongs to A or B sublattice) in a unit cell. For tA = 0, tB = 0, and η = 0, the parameters in the Hamiltonian (6) become

and there is no longer need to distinguish sublattice A or sublattice B. With the Hamiltonian (6) is reduced to

which agrees with Kitaev model.

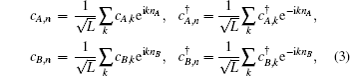
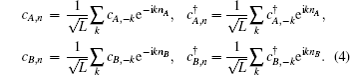
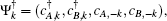
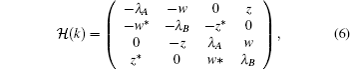
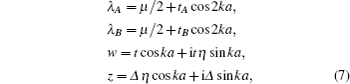
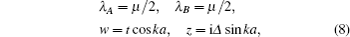
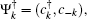
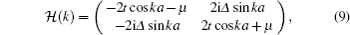
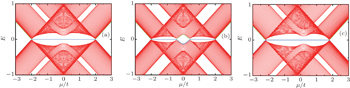
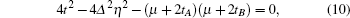
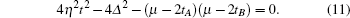
The energy eigenvalues of the system can be obtained by diagonalizing the Hamiltonian (6). Then it shows that the gap closes only at k = 0 while

and k = π/2a while

For a gapped noninteracting fermion system, the topological class is determined by symmetry and spatial dimension.[28–30] In this spinless fermion system, the time-reversal operator is defined by T = 𝒦, where 𝒦 is the complex-conjugation operator.[28,29] The model has the time-reversal symmetry

for all the parameters t, tA, tB, μ, Δ, and η are real. The chiral symmetry of the model is represented by the operator C for

where

where σ are Pauli matrices and I2 is 2 × 2 identity matrix. Finally, the particle–hole symmetry operator is

and the model has the particle–hole symmetry

With the time-reversal, chiral and particle–hole symmetry, the topological class of the model is BDI.[29]

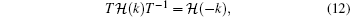
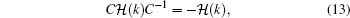
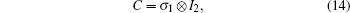
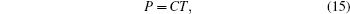
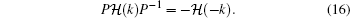
For the case of μ = 0, tA = 0, and tB = 0, there is another chiral symmetry operator C′, which is given by

that satisfies C′ℋ(k)C′−1 = −ℋ(k), and the particle–hole symmetry is represented by the operator P′ = C′T. In the above equation, τ are Pauli matrices.

With the symmetries P′, C′, and T, the system also belongs to BDI class. The class with the symmetry P′, C′, and T is associated with zero energy modes of soliton while the class with the symmetry P, C, and T is associated with Majorana zero energy modes.[26]

3. Phase diagram

To discuss the topological properties of the system, we can define a winding number as

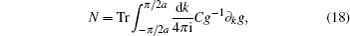
with g = −ℋ(k)−1 is the Green’s function of zero energy. This winding number is associated with the chiral index of Majorana zero modes.[41,42]

For the chiral operator C, we can choose a unitary transformation

which is associated with the following Majorana operators:

Then we can block off-diagonalize the Hamiltonian (6), i.e.,

where

Then the winding number becomes

The winding number N changes only at the singular points where Z(k) = detQ(k) = 0, thus we can obtain that the phase transition only occurs at k = 0 and k = π/2a. Meanwhile, we can get that N = ±1 (1 for Δ > 0; −1 for Δ < 0) in the topological region with Z(0)Z(π/2a) < 0 while N = 0 in the trivial region with Z(0)Z(π/2a) > 0. The Z(0) and Z(π/2a) are given respectively by

The phase boundary obtained from Z(0) = 0 and Z(π/2a) = 0 agrees with the results (10) and (11) respectively. That is, the change of phase transformation points which is caused by the NNN hopping can be described by a shift of chemical potential. The phase diagram is shown in Fig. 1.

Fig. 1. The phase diagram of the model. The phase boundary in which the gap closes are obtained from Z(0) = 0 and Z(π/2a) = 0. The parameters are chosen as: (a) tA = 0, tB = 0; (b) tA = 0.1t, tB = −0.1t; (c) tA = 0.5t, tB = 0.5t; (d) tA = 1.25t, tB = 0.8t, respectively. The change of phase transformation points which is caused by the NNN hopping can be described by a shift of chemical potential.

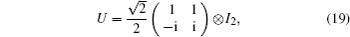
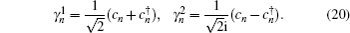
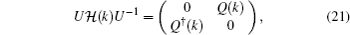
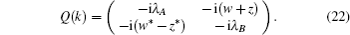
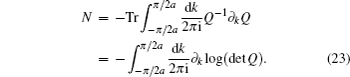
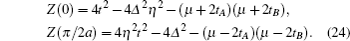
With addition of the nonzero NNN hopping, the symmetries P′ and C′ are broken, therefore there are no zero energy modes of soliton and the edge modes are Majorana zero energy modes.[26]

4. Numerical results

In a finite chain, the energy spectrum of the system can be obtained by diagonalizing the Hamiltonian (1). Illustratively, we show the energy spectrum with length L = 64 in Fig. 2. The midgap states with zero energy emerge in the topological region for non-vanishing winding number N and disappear in the trivial region for vanishing N.

Fig. 2. The energy spectrum of a finite chain (L = 64). The parameters are chosen as: (a) Δ = 0.2t, η = 0.1, tA = 0, tB = 0; (b) Δ = 0.1t, η = 0.2, tA = 0.1t, tB = −0.1t; (c) Δ = 0.2t, η = 0.1, tA = 0.1t, tB = 0.1t, respectively. The two middle eigenvalues are plotted in green (blue) while other energy eigenvalues are in red. The zero energy modes emerge in the topological region.

Figure 3 shows the localization of the probability density. Since the wave functions corresponding to the zero energy modes in the topological region are concentrated at the edges, the zero energy modes are edge states. In the trivial region the middle states delocalize over the whole chain. The results shown in Figs. 2 and 3 characterize the topological properties of the system and agree with the analytical results in Section 3.

Fig. 3. Localization of the wave function corresponding to the middle eigenvalue (green plot in Fig. 2). The parameters are chosen as: (a) Δ = 0.2t, η = 0.1, tA = 0, tB = 0; (b) Δ = 0.1t, η = 0.2, tA = 0.1t, tB = −0.1t; (c) Δ = 0.2t, η = 0.1, tA = 0.1t, tB = 0.1t, respectively. The wave functions are concentrated at the edges in the topological region and delocalize over the whole chain in the trivial region (right).

In order to study the topological properties of the system with the interaction term

we calculate the entanglement spectrum, the degeneracy of which corresponds to the gapless edge modes with the open boundary condition. The entanglement spectrum[32] is defined as

where Pα is the eigenvalue spectrum of reduced density matrix. In the canonical form[43,44] of the MPS, the ground-state wave function is expressed as

and the entanglement spectrum can be obtained by

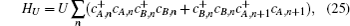
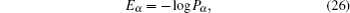
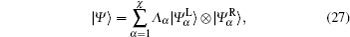
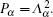
With the iTEBD numerical method,[39,40] based on the MPS formalism, the ground state of the system and entanglement spectrum can be effectively calculated.

In order to construct the MPS and employ the iTEBD method, we need to do a Jordan–Wigner transformation under which the Hamiltonian becomes

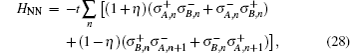
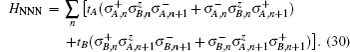
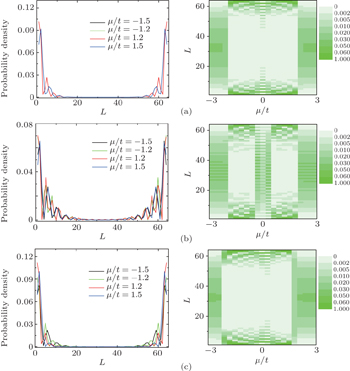
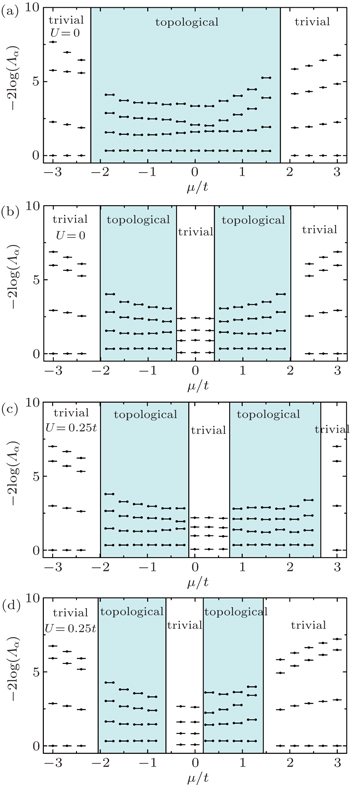
The entanglement spectrum in the non-interacting case is shown in Figs. 4(a) and 4(b). The entanglement spectrum is 2-fold degenerate in the topological region while non-degenerate in the trivial region.

The interaction term reads (after doing a Jordan–Wigner transformation)

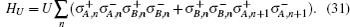
Then we can calculate the ground state, phase boundary, and entanglement spectrum by employing the iTEBD method.

With addition of small NN electron–electron interactions, the 2-fold degeneracy of the entanglement spectrum does not disappear, and the phase boundary has changed as illustratively shown in Figs. 4(c) and 4(d).

Because of 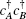and cAcB terms in the Hamiltonian, the system does not conserve total particle number. With the repulsive interaction, the average particle number per site effectively decreases[45] while it effectively increases with the attractive interaction. For the −μN term in Hamiltonian, the change of average particle number will induce an effective chemical potential which lifts the zero energy modes of soliton and changes the boundary of the topological phase, as shown in Fig. 4.

Fig. 4. The entanglement spectrum. Panels (a) and (b) are non-interacting cases for U = 0 while panels (c) and (d) are U = 0.25 and U = −0.25. Other parameters are chosen as: (a) Δ = 0.2t, η = 0.1, tA = 0.1t, tB = 0.1t; (b), (c), and (d) Δ = 0.1t, η = 0.2, tA = 0.1t, tB =−0.1t, respectively.
5. Conclusions

In this paper, we have studied the effects of the NNN hopping and NN interactions on the topological phases in a one-dimensional dimerization Kitaev model. For the symmetry discussed with Bogoliubov–de Gennes form, the topological class of the model is BDI. By defining a topological number, we obtain the phase diagram of the model without interaction, which shows that the change of phase transformation points which is caused by the NNN hopping can be described by a shift of chemical potential. With the electron–electron NN interactions, the topological phase boundary changes with the addition of an effective chemical potential which can be explained by the change of the average particle number.

Reference
1Wen X G 1989 Phys. Rev. 40 7387
2Wen X GNiu Q 1990 Phys. Rev. 41 9377
3Wen X G 1990 Int. J. Mod. Phys. 04 239
4Landau L D1937Phys. Z. Sowjetunion1126
5Ginzburg V LLandau L D1950Zh. Ekaper. Teoret. Fiz.201064
6Kitaev A Y 2001 Phys.-Usp. 44 131
7Qi X LZhang S C 2011 Rev. Mod. Phys. 83 1057
8Alicea J 2012 Rep. Prog. Phys. 75 076501
9Leijnse MFlensberg K 2012 Semicond. Sci. Technol. 27 124003
10Beenakker C W J 2013 Annu. Rev. Con. Mat. Phys. 4 113
11Cai XLang L JChen SWang Y 2013 Phys. Rev. Lett. 110 176403
12Wang PSun Q FXie X C 2014 Phys. Rev. 90 155407
13Fu LKane C L 2008 Phys. Rev. Lett. 100 096407
14Lutchyn R MSau J DDas Sarma S 2010 Phys. Rev. Lett. 105 077001
15Oreg YRefael Gvon Oppen F 2010 Phys. Rev. Lett. 105 177002
16Stanescu T DLutchyn R MDas Sarma S 2011 Phys. Rev. 84 144522
17Liu YMa ZZhao Y FMeenakshi SWang J 2013 Chin. Phys. 22 067302
18Shang E MPan Y MShao L BWang B G 2014 Chin. Phys. 23 507201
19Zhang D PTian G S 2015 Chin. Phys. 24 080401
20Mourik VZuo KFrolov S MPlissard S RBakkers E P A MKouwenhoven L P 2012 Science 336 1003
21Rokhinson L PLiu XFurdyna J K 2012 Nat. Phys. 8 795
22Das ARonen YMost YOreg YHeiblum MShtrikman H 2012 Nature Phys. 8 887
23Deng M TYu C LHuang G YLarsson MCaroff PXu H Q 2012 Nano Lett. 12 6414
24Lee E J HJiang XAguado RKatsaros GLieber C MDe Franceschi S 2012 Phys. Rev. Lett. 109 186802
25Nadj-Perge SDrozdov I KLi JChen HJeon SSeo JMacDonald A HBernevig B AYazdani A 2014 Science 346 602
26Wakatsuki REzawa MTanaka YNagaosa N 2014 Phys. Rev. 90 014505
27Altland AZirnbauer M R 1997 Phys. Rev. 55 1142
28Schnyder A PRyu SFurusaki ALudwig A W W 2008 Phys. Rev. 78 195125
29Kitaev A 2009 AIP Conf. Proc. 1134 22
30Ryu SSchnyder A PFurusaki ALudwig A W W 2010 New J. Phys. 12 065010
31Read NGreen D 2000 Phys. Rev. 61 10267
32Li HHaldane F D M 2008 Phys. Rev. Lett. 101 010504
33Pollmann FTurner A MBerg EOshikawa M 2010 Phys. Rev. 81 064439
34Fidkowski L 2010 Phys. Rev. Lett. 104 130502
35Östlund SRommer S 1995 Phys. Rev. Lett. 75 3537
36Verstraete FWolf M MCirac J I2007Quantum Inf. Comput.7401
37Zheng DZhang G MXiang TLee D H 2011 Phys. Rev. 83 014409
38Zhu J M2008Chin. Phys. Lett.2513574
39Vidal G 2007 Phys. Rev. Lett. 98 070201
40Orus RVidal G 2008 Phys. Rev. 78 155117
41Sato MTanaka YYada KYokoyama T 2011 Phys. Rev. 83 224511
42Tewari SSau J D 2012 Phys. Rev. Lett. 109 150408
43Vidal G 2003 Phys. Rev. Lett. 91 147902
44Shi Y YDuan L MVidal G 2006 Phys. Rev. 74 022320
45Sticlet DSeabra LPollmann FCayssol J 2014 Phys. Rev. 89 115430