Cite this Article
Hossein Asadpour Seyyed, Solookinejad G, Panahi M, Ahmadi Sangachin E. Optical bistability and multistability in a defect slab doped by GaAs/AlGaAs multiple quantum wells. Chinese Physics B, 2016, 25(5): 054208  
Permissions
Optical bistability and multistability in a defect slab doped by GaAs/AlGaAs multiple quantum wells
Hossein Asadpour Seyyed†, , Solookinejad G, Panahi M, Ahmadi Sangachin E
Department of Physics, Marvdasht Branch, Islamic Azad University, Marvdasht, Iran

 

† Corresponding author. E-mail: S.Hosein.Asadpour@gmail.com

Abstract
Abstract

We proposed a new model for controlling the optical bistability (OB) and optical multistability (OM) in a defect slab doped with four-level GaAs/AlGaAs multiple quantum wells with 15 periods of 17.5 nm GaAs wells and 15-nm Al0.3 Ga0.7As barriers. The effects of biexciton energy renormalization, exciton spin relaxation, and thickness of the slab on the OB and OM properties of the defect slab were theoretically investigated. We found that the transition from OB to OM or vice versa is possible by adjusting the controllable parameters in a lab. Moreover, the transmission, reflection, and absorption properties of the weak probe light through the slab were also discussed in detail.

PACS: 42.50.–p;42.65.pc;
Keyword:optical bistability;optical multistability;quantum well nanostructure;
1. Introduction

In the last few decades, the theoretical and experimental studies related to quantum coherence and quantum interference based phenomena, such as electromagnetically induced transparency (EIT),[1–3] lasing without inversion,[4] giant Kerr nonlinearity,[5–7] four-wave mixing,[8,9] and so on,[10–17] have been carried out in multi-level atomic systems. In quantum and nonlinear optics, optical bistability (OB) and optical multistability (OM) due to their important applications in quantum memories, all-optical switching, and logic circuits[18] have been discussed by several groups.[19–32] It is worth pointing out that the general method for analyzing the optical bistability is based on the feedback mechanism in the unidirectional ring cavity confined with atomic samples.[19–32] Joshi et al.[19] discussed experimentally the optical bistable behavior in an optical ring cavity filled with a collection of three-level Λ-type rubidium atoms interacting with two collinearly propagating laser beams. They found that the bistability is very sensitive to the induced atomic coherence in this system and, thus, can be easily controlled by changing the intensity and the frequency detuning of the coupling field. Then, many models have been proposed for analyzing the OB and OM in multi-level atomic systems via laser coherent fields,[20–22] spontaneously generated coherence (SGC),[23–26] the injection of squeezed light,[27] the atomic cooperation parameter,[28] and so on. For example, Xiao and Kim[22] investigated the OB in an optical system which consists of a four-level atomic system with a microwave drive field and an optical cavity. They found that the OB can be accomplished by adjusting different physical parameters in both steady and transient processes. They showed that due to the existence of the microwave drive field, the optical bistability can also be obtained even under the weak coherent coupling field condition. The quantum interference effect from incoherent pumping field and spontaneous emission on OB properties in a V-type three-level atomic system confined in a unidirectional ring cavity was investigated in Ref. [29]. It was found that the OB can be controlled by the rate of the incoherent pumping field and by the interference mechanism arising from the spontaneous emission and the incoherent pumping field. Polarized control of OB in a four-level tripod atomic system has been discussed in Ref. [30]. It was demonstrated that the OB behaviors can be controlled efficiently by adjusting the system parameters and the relative phase of the applied fields. Wang et al.[31] proposed a model for manipulating the OB in an open three-level Λ-type atomic system confined in a unidirectional ring cavity. They found that the OB behaviors can be controlled by the incoherent pumping rate and the spontaneously generated coherence.

It should be noted that quantum coherence and quantum interference can lead to manipulation of nonlinear quantum optical phenomena in the semiconductor quantum wells (SQWs) and quantum dots (SQDs).[33–46] The OB behaviors of a three-level quantum well nanostructure confined in a unidirectional ring cavity have been studied.[33] In another study,[34] the absorptive-dispersive OB behavior via tunable Fano-type interference based on the intersubband transitions in asymmetric double quantum wells driven coherently by a probe laser field by means of a unidirectional ring cavity has been analyzed. It was shown that the OB can be controlled efficiently by tuning the energy splitting of the two excited states (the coupling strength of the tunnelling), the Fano-type interference, and the frequency detuning. The influence of the electronic cooperation parameter on the OB behavior has also been discussed. In another study, Li[35] analyzed the OB properties of an asymmetric coupled-quantum well based on the intersubband transitions driven coherently by a probe laser field and a control laser field by means of a unidirectional ring cavity. It was demonstrated that the OB can be controlled by tuning the energy splitting between two tunnel-coupled electronic levels, the intensity of the control field, and the frequency detuning of the probe and the control fields. The SQW and SQD due to their wide potential applications in optoelectronics and solid-state quantum information science have been analyzed by many research groups.[47–49] The large electric dipole moments due to the small effective electron mass, the great flexibilities in device design by choosing the materials and the structure dimensions, and the high nonlinear optical coefficients make these structures have advantages over the atomic systems. Very recently, Yang et al.[47] discovered control of the Goos–Hänchen (GH) shift of a mid-infrared probe beam in a cavity consisting of an asymmetric double quantum well nanostructure. They obtained the maximum negative and positive GH shifts in transmitted and reflected light when the quantum interference from electron tunneling was considered.

Unlike the general method for achieving the optical bistability, we propose a new model for analyzing the optical bistability in a dielectric medium with a defect layer of multiple quantum well nanostructure. By using the transform matrix method, we calculate the transmission and reflection coefficients of the incident probe light to the defect slab, and then discuss the OB behaviors of the transmitted light through the defect slab. To the best of our knowledge, there are no theoretical or experimental works related to OB and OM in a slab with a defect layer of multiple quantum well nanostructure. We will discuss the effects of the biexciton energy renormalization, the exciton spin relaxation, and the thickness of the slab medium on the OB and OM behaviors of the incident light. Here, the structure of multiple quantum wells is based on that in Ref. [50]; however, our work is drastically different from that work. First and foremost is that we are interest in showing the controllability of OB and OM in a defect slab. Second, the thickness of the slab is considered as a new parameter for controlling the OB and OM behaviors of the weak probe light.

2. Model and equations
2.1. Pulse propagation

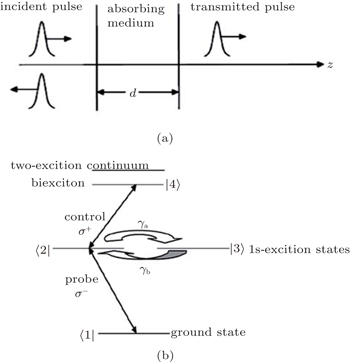
In the following, the pulse propagation in a slab and the structure of the doped MQWs in the defect layer of the slab will be discussed. It is assumed that the incident pulse normally propagates through the dielectric medium along the z direction (Fig. 1(a)). The extension of the slab is infinite in the x–y plane and finite from z = 0 to z = d, and outside of the slab is a vacuum. For the electric and magnetic components of a monochromatic wave of frequency ωp through the slab, the transform matrix can be expressed as

where the refractive index of the slab (n(ωp)) is related to the dielectric function (ɛ(ωp)) through The reflection coefficient r(ω) and transmission coefficient t(ω) can be obtained as

The slab considered here is composed of a constant dielectric material doped by GsAs MQWs (17.5 nm GaAs wells and 15 nm Al0.3Ga0.7 barriers). Therefore, the dielectric function ɛ(ωp) of the slab can be influenced by the doped MQWs. In this case, the dielectric function has two parts

Here, ɛb is the background dielectric constant and χ(ωp) denotes the susceptibility of the doped MQWs. From Eqs. (2) and (3), one can find that the reflection and transmission coefficients depend on the thickness and the dielectric function of the slab. Under the resonance condition, the thickness of the slab is employed as whereas, under the off-resonance condition, it is considered as Here, m is an integer and is chosen to be m = 80 for the theoretical calculations.

Fig. 1. (a) Schematic of the weakly absorbing dielectric slab. (b) Schematic energy-level diagram of the GaAs multiple quantum wells.
2.2. GaAs multiple quantum well nanostructure

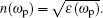
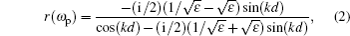
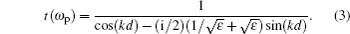
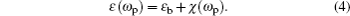
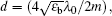
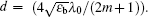
We consider the MQWs as a dispersive layer in the dielectric slab and study its level structure. The energy levels of the GaAs MQWs form a four-level system where a control beam drives the transition |2〉 → |3〉 while a weak probe beam couples to the transition |1〉 → |2〉 (Fig. 1(b)). In other words, the control beam drives the 1s-exciton state to biexciton transition and the weak probe beam couples ground state |1〉 to the 1s-exciton state. By focusing on the interband transitions between the conduction bands with spin Sz = ±1/2 and the heavy-hole (HH) valance bands with mj = ±3/2 in the GaAs MQWs, an effective four-level configuration is obtained. By using σ+ and σ− circularly polarized light, the spin-up |+〉 (σ+ transition) and spin-down |−〉 (σ− transition) excitonic transitions can be excited, respectively. The biexciton (two-exciton states) state (Fig. 1(b)) can be formed by the correlations between the two excitons with opposite spins via the Coulomb interaction. It has been shown that the biexciton coherence induces a destructive interference in the GaAs MQWs and can be raised from the coherent superposition between the ground and biexciton states.[51,52] Under the rotating wave approximation, the set of density matrix equations can be obtained for the four-level system as follows:

where ρ21 and ρ41 describe the exciton and the biexciton coherences, respectively, Δp = ωp − ωx and Δc = ωc − ωb are the detuning parameters of Rabi frequencies Ωp and Ωc, respectively, ωx (ωb) and γ3,4 (γ1,2) are the resonance frequency and the decay rate of the exciton (biexciton) coherence, γa,b is the exciton spin relaxation between the 1s-exciton states, ωc(ωb) and Ωc (Ωp) are the optical frequency and the Rabi frequency of the control (probe) field. The biexciton binding energy is cited from Ref. [53] and can be changed by the size of the MQWs.[54] In order to derive the susceptibility, we need to obtain the steady state solution of the density matrix equations. The susceptibility of the probe field of the medium can be determined as

The real and imaginary parts of the susceptibility correspond to the dispersion and absorption, respectively. Equations (2) and (3) along with Eqs. (4)–(6) relate to the absorption and the gain properties of the weak probe field through the slab.

3. Results and discussion

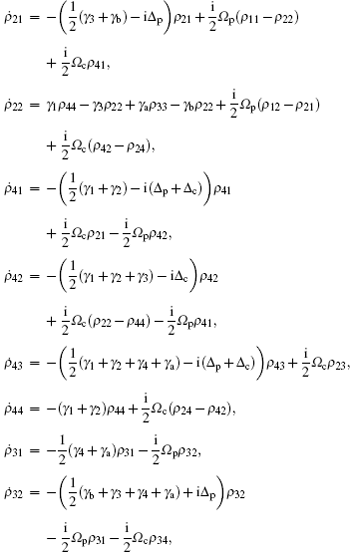
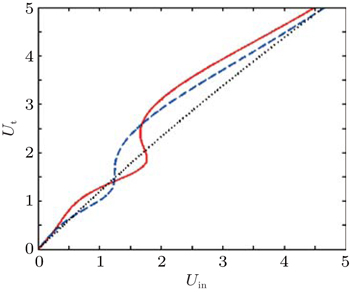
To investigate the OB behavior of the slab, one can use the relationship between the incident intensity Uin and the transmitted intensity Ut

where T denotes the transmission coefficient of the slab and can be obtained by Eq. (3). The numerical results of the transmitted intensity Ut versus the incident intensity Uin are shown in Figs. 2–7. The parameters used are ɛb = 4, λ0 = 1.55 μm, Δp = 0.5, Δc = 0, γi = 1.

Fig. 2. The transmitted intensity of the probe field Ut versus the incident intensity Uin for different coupling fields. The solid line corresponds to Ωc = 0.2, dashed line corresponds to Ωc = 2, and dotted line corresponds to Ωc = 5. The other selected parameters used are ɛb = 4, λ0 = 1.55 μm, Δp = 0.5, Δc = 0, γi = 1, γa = γb = 0, and β = 0.
Fig. 3. Transmission (solid), reflection (dashed), and absorption (dotted) properties of the incident light versus probe detuning for (a) Ωc = 0.2, (b) Ωc = 2, and (c) Ωc = 5. The selected parameters are the same as those in Fig. 2.
Fig. 4. (a) The transmitted intensity of the probe field Ut versus the incident intensity Uin for γb = γa = 0 (solid) and γb = γa = 1 (dashed). (b) Transmission (solid), reflection (dashed), and absorption (dotted) properties of the incident light versus detuning of the probe light in the presence of exciton spin relaxation. The used parameters are the same as those in Fig. 2 and Ωc = 0.2.
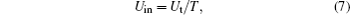
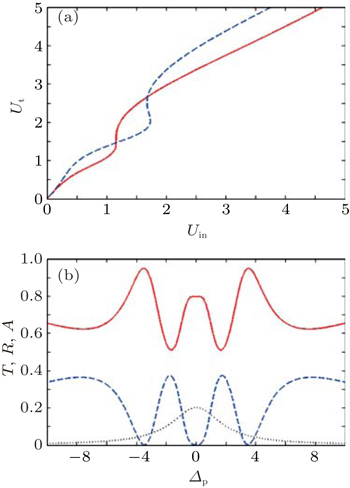
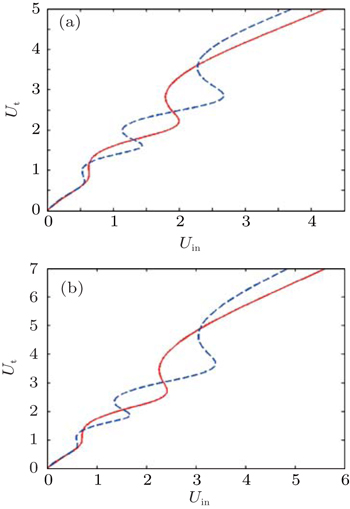Fig. 5. The transmitted intensity of the probe field Ut versus the incident intensity Uin for (a) m = 100 and (b) m = 150. The selected parameters are the same as those in Fig. 2.
Fig. 6. (a) The transmitted intensity of the probe field Ut versus the incident intensity Uin for β = 0, (solid) and β = 1 (dashed). (b) Transmission (solid), reflection (dashed) and absorption (dotted) properties of the incident light versus detuning of the probe light in the absence of exciton spin relaxation. The used parameters are the same as those in Fig. 2 and Ωc = 2.
Fig. 7. Transmission (solid), reflection (dashed), and absorption (dotted) properties of the incident light versus detuning of the probe light for (a) m = 100 and (b) m = 150. The selected parameters are γb = γa = 1, β = 1, Ωc = 2 and the others are the same as those in Fig. 2.

The effect of coherent coupling on the OB behavior of the probe field is investigated in Fig. 2. It can be seen that the threshold of OB decreases when we change parameter Ωc from 0.2 (solid) to 2 (dashed). When we increase Ωc to 5 (dotted), the bistable behavior vanishes and the slab does not show the bistable behavior. The transmission (solid), reflection (dashed), and absorption (dotted) of the weak probe light through the slab for different coupling fields are displayed in Fig. 3. One can see that when Ωc = 0.2 (Fig. 3(a)), the transmission coefficient reaches 1, the reflection coefficient is 0, and the transparency window is very narrow. By increasing Ωc to 2 (Fig. 3(b)) and 5 (Fig. 3(c)), the transparency window becomes wide. For all these values, the transmission and reflection coefficients have similar behaviors.

In Fig. 4(a), we display the effect of the exciton spin relaxation on the OB behaviors of the probe field in the dielectric slab. It is clearly shown that in the presence of the exciton spin relaxation, the threshold of OB increases. Considering the transmission (solid), reflection (dashed), and absorption (dotted) of the weak probe light through the slab (Fig. 4(b)), we can find that the transmission reduces and the absorption increases. In other words, the exciton spin relaxation is a decoherence process and annihilates the quantum coherence in the slab.

In the next section, we study the effect of the thickness of the slab on the OB behavior of the probe field. The OB behavior of the probe field for different thicknesses in the absence and presence of the exciton spin relaxation is displayed in Fig. 5. We find that the thickness of the slab has a major role in switching OB to OM. So, by increasing the thickness of the slab, the OB can be converted to the OM. Moreover, we find that the threshold of OM increases in the presence of the exciton spin relaxation.

In the following, we analyze the effect of the biexciton energy renormalization on the OB behavior of the probe field in the slab. The effects of the biexciton energy renormalization can be simulated by replacing ωb with in Eq. (5) at low intensity for the σ+ polarized control field. Here, β is a phenomenological constant and the energy renormalization for the σ− exciton can be ignored. It has been shown that the biexciton energy renormalization can be adjusted by controlling the size of the multiple quantum well nanostructure.[54] Therefore, the biexciton binding energies are different for various quantum well nanostructures of different sizes. From Fig. 6(a), we can see that when we change parameter β from 0 to 1.5, the intensity threshold of OB increases. The transmission (solid), reflection (dashed), and absorption (dotted) of the probe light through the slab for β = 1.5 are displayed in Fig. 6(b). It is found that the transparency window vanishes and an absorptive peak appears in the absorption curve of the probe light. In this case, the transmission coefficient reduces and reaches 0.8, while the reflection coefficient remains constant.

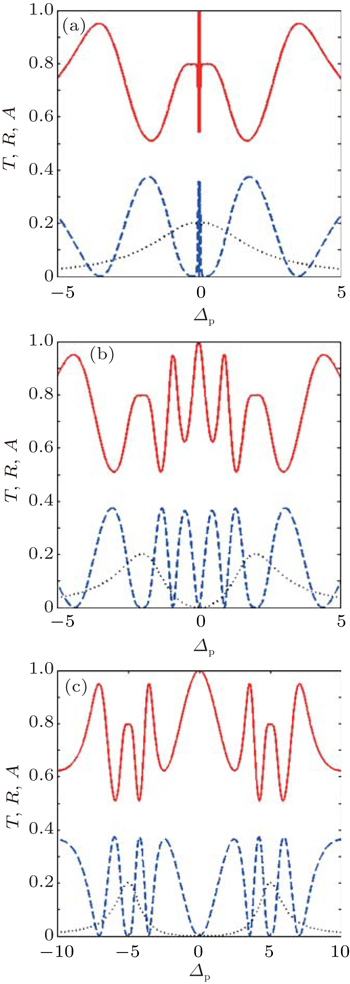
Finally, we plot the transmission (solid), reflection (dashed), and absorption (dotted) of the probe light for m = 100 and m = 150 in the presence of the exciton spin relaxation and biexciton binding energy in Fig. 7. It can be seen that the absorption coefficient is fixed for different thicknesses of the slab; however, the transmission and reflection coefficients can be changed by adjusting the thickness of the slab. According to Agarwal’s reciprocity theorem,[55] in a lossless slab, each peak (dip) in reflection or transmission shows subluminal (superluminal) light propagation. In superluminal light propagation, the group velocity of the light pulse can exceed the velocity of light in a vacuum and even becomes negative. Note that such behaviors do not violate Einstein’s special theory of relativity.[56] Based on the above discussion, we can find that by changing the thickness of the slab, the switching from subluminal (superluminal) light reflection (transmission) to superluminal (subluminal) light reflection (transmission) can occur.

4. Conclusion

We investigated the OB and OM behaviors of the four-level multiple quantum well nanostructure inside a dielectric slab. We found that by adjusting some controllable parameters such as the intensity of the coupling field, the exciton spin relaxation, the biexciton binding energy, and the thickness of the slab, the intensity threshold of OB can be controlled, and for some parameters, the switching between OB and OM can occur. Moreover, the transmission, reflection, and absorption of the weak probe light through the cavity have been discussed. We found that the switching from subluminal to superluminal or vice versa can be obtained for the reflected and transmitted light from the slab.

Reference
1Harris S E1997Phys. Today5036
2Wu S FMao LJones A MYao WZhang C WXu X D 2012 Nano Lett. 12 2032
3Wu YYang X 2005 Phys. Rev. 71 053806
4Zhao YHuang DWu C 1996 J. Opt. Soc. Am. B: Opt. Phys. 13 1614
5Sahrai MAsadpour S HSadighi-Bonabi R2010JNOPM19503
6Hamedi H RAsadpour S HSahrai M 2013 Optik 124 366
7Asadpour S HSahrai MSoltani AHamedi H R 2012 Phys. Lett. 376 147
8Wu YDeng L 2004 Phys. Rev. Lett. 93 143904
9Wu YYang X 2004 Phys. Rev. 70 053818
10Wang ZJiang J 2010 Phys. Lett. 374 4853
11Wu YYang X 2005 Phys. Rev. 71 053806
12Si L GYang W XYang X 2009 JOSA 26 478
13Wu YYang X 2007 Phys. Rev. 76 054425
14Wang ZShui TYu B2014Opt. Commun.315263
15Si L GYang W XLou X YHao X YYang X 2010 Phys. Rev. 82 013836
16Wu YYang X 2007 Appl. Phys. Lett. 91 094104
17Wang ZYu B 2014 Laser Phys. Lett. 11 035201
18Gibbs H MMcCall S LVenkatesan T N C 1976 Phys. Rev. Lett. 36 1135
19Joshi ABrown AWang HXiao M 2003 Phys. Rev. 67 041801
20Wang ZXu M 2009 Opt. Commun. 282 1574
21Asadpour S HEslami-Majd A 2012 J. Lumin. 132 1477
22Xiao Z HKim K 2010 Opt. Commun. 283 2178
23Joshi AYang WXiao M 2003 Phys. Rev. 68 015806
24Lu X YLi J HBing L JMing L J 2006 J. Phys. 39 5161
25Osman K I 2006 Opt. Commun. 259 194
26Joshi AXiao M 2010 J. Modern Opt. 57 1196
27Chen ZDu CGong SXu Z 1999 Phys. Lett. 259 15
28Li J HLou X YLuo J MHuang Q J 2006 Phys. Rev. 74 035801
29Sahrai MAsadpour S HSadighi-Bonabi 2011 J. Lumin. 131 2395
30Zhang DLi J HDing CYang X 2012 Phys. Scr. 85 045401
31Wang ZChen A XBai YYang W XLee R K 2012 J. Opt. Soc. Am. 29 2891
32Zhu ZChen A XYang W XLee R K 2014 J. Opt. Soc. Am. 31 2061
33Joshi AXiao M 2004 Apply. Phys. 79 65
34Li J HYang X 2006 Eur. Phys. J. 53 449
35Li J H 2007 Opt. Commun. 274 366
36Asadpour S HHamedi H REslami Majd ASahrai M2011Physica E44464
37Wang AZhen SWu XZhu JCao ZYu B 2013 J. Lumin. 143 605
38Yang W XChen A XLee R KWu Y 2011 Phys. Rev. 84 013835
39Asadpour S HRahimpour Soleimani H 2014 Opt. Commun. 315 347
40Asadpour S HGolsanamlou ZRahimpour Soleimani H 2013 Physica 54 45
41Li J H 2007 Phys. Rev. 75 155329
42Yang XLi Z WWu Y 2005 Phys. Lett. 340 320
43Wang ZYu B 2013 J. Opt. Soc. Am. 30 2915
44Asadpour S HJaberi MRahimpour Soleimani H 2013 J. Opt. Soc. 30 1815
45Asadpour S HRahimpour Soleimani H 2014 Opt. Commun. 315 394
46Chen A 2014 Opt. Express 22 26991
47Yang W XLiu SZhu ZZiauddinLee R K 2015 Opt. Lett. 40 3133
48Yang W X 2015 Opt. Lett. 40 4903
49Yang W XXu JLee R K2009Modern Phys. Lett. B232215
50Asadpour S HRahimpour Soleimani H 2015 Opt. Quant. Electron 47 401
51Wang HShah JDamen TPfeiffer C 1994 Solid. State Commun. 91 869
52Cheng G 2002 Phys. Rev. Lett. 88 117901
53Waldmuller I 2004 Phys. Rev. 69 205307
54DalSavio CPierz KAde GDanzebrink H UGobel W OHangleiter A 2006 Appl. Phys. 84 317
55Agarwal G SGupta D 2002 Opt. Lett. 27 1205
56Gauthier D JBoyd R W2007Photon Spectra4182