† Corresponding author. E-mail:
Project supported by the Natural Science Foundation of Jiangsu Province, China (Grant No. KYLX_0341) and the National Natural Science Foundation of China (Grant No. 61405147).
In pulsed laser drilling, melt ejection greatly influences the keyhole shape and its quality as well, but its mechanism has not been well understood. In this paper, numerical simulation and experimental investigations based on 304 stainless steel and aluminum targets are performed to study the effects of material parameters on melt ejection. The numerical method is employed to predict the temperatures, velocity fields in the solid, liquid, and vapour front, and melt pool dynamics of targets as well. The experimental methods include the shadow-graphic technique, weight method, and optical microscope imaging, which are applied to real-time observations of melt ejection phenomena, measurements of collected melt and changes of target mass, observations of surface morphology and the cross-section of the keyhole, respectively. Numerical and experimental results show that the metallic material with high thermal diffusivity like aluminum is prone to have a thick liquid zone and a large quantity of melt ejection. Additionally, to the best of our knowledge, the liquid zone is used to illustrate the relations between melt ejection and material thermal diffusivity for the first time. The research result in this paper is useful for manufacturing optimization and quality control in laser-material interaction.
The laser becomes an important tool in modern material processing and manufacturing since it has high energy density and small divergence.[1–5] Laser drilling, as one of the main laser processing techniques, is broadly used in mechanics and electronics.[6,7] However, recent industry demands improvements in manufacturing quality calling for a better understanding of the drilling process for manufacturing optimization and quality control. In laser drilling, when power density ranges from 5 MW/cm2 to 50 MW/cm2, different physical processes such as heating, melting, vaporization, as well as melt ejection, function together to generate the keyhole.[8] Among these processes, melt ejection has the greatest influence on keyhole shape and its quality. Therefore, studies on the melt ejection mechanism can provide a useful reference for keyhole quality control and improvement in laser drilling.
Experimental research is a direct way to observe the phenomena of melt ejection. Even early in the 1980s, dynamics of melt ejection during irradiation with CO2 laser was studied.[9] In these years, higher-performance devices have been widely used to investigate the dynamical process of melt ejection with higher spatial and time resolution. Low et al.[10–12] observed the melt ejection in laser drilling on both dielectrics and metals. It was concluded that melt ejection is mostly dependent on the parameters of laser pulses. Based on these studies, more detailed researches have been conducted recently. Voisey et al.[13] considered more characteristics of melt ejection, and proved that melt ejection is mainly induced by the molten material flows along the keyhole wall. Duan et al.[7] carefully analyzed the influences of pulse width, pulse energy, pulse repetition rate, trepanning velocity, trepanning diameter, beam rotation number, and assist gas pressure on melt ejection. Besides, more papers focused on the melt ejections of different targets: Trippe et al.,[14] Chen et al.,[15] and Zhang et al.[16] observed the melt ejection dynamics in keyholes generated during laser drilling on steel, molybdenum and glass, respectively. Though with direct observation and accurate measurement, the phenomena of melt ejection can be truly described, the melt ejection mechanism is still poorly understood.
Compared with experimental observation, modeling approaches propose a route to exploring the physical process of melt ejection in laser drilling. Usually the keyhole model of laser drilling is established by analytical and/or numerical method.[17–26] Low et al.[17] investigated the influence of laser pulses on melt ejection, which is complementary to the experimental results.[11,12] Song et al.[18] presented the temperature distributions and mushy zone size near the keyhole wall, which is useful to study the formation of the vapour jet and melt ejection. Muhammad et al.[19] studied the melt ejection in pulsed laser dry and wet micromachining processes. Solana et al.[20] explained that the melt ejection occurs in both initial and steady states in the whole process of laser drilling.
Though these results are helpful to understand melt ejection in laser manufacturing, few reported results focus on the influence of targets on ejection. Bandyopadhyay et al.[27] and Hugger et al.[28] have compared the different melt ejection results with different alloys, however, the influencing factors of material properties on melt ejection are still not discussed in detail.
In laser manufacturing, a large number of metal materials have been used for processing. However, in industry, the influence of material property on the final drilling quality is still empirical. Understanding the influence of target parameters on melt ejection is rather important. Here, in this paper, a great effort is made to profoundly and comprehensively investigate the effects of material properties on melt ejection, with a novel two-dimensional (2D) transient multiphase model based on modified hydrodynamic equations and improved level-set technique, and multi-aspect experimental methods including the shadowgraphic technique, weight method, and optical microscope imaging. Two kinds of typical metal materials: 304 stainless steel and aluminum are chosen as our targets. The simulation results accord well with the experimental data. The research results demonstrate that the metal with high thermal diffusivity such as aluminum is prone to have a thick molten layer and a large quantity of melt ejection in the drilling process. The research result in this paper can serve as a useful guidance for manufacturing optimization and quality control in laser surface treatment,[29] cladding,[30,31] cutting,[32] welding,[33,34] and drilling.
In order to study the mechanism of melt ejection in laser drilling, an improved transient model based on the finite element method, level set technique,[35–40] and hydrodynamic equations is used for detailed analysis. The original mathematical model of laser drilling can be described by the following continuity equation, Navier–Stokes equation, level set equation, and energy conservation equation, respectively,


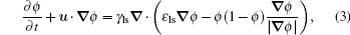
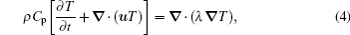
In traditional models, the continuity equation shown in Eq. (

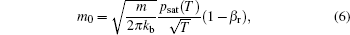
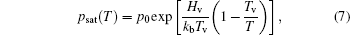
The original Navier–Stokes equation shown in Eq. (
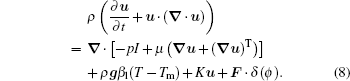

It is worth noting that in our improved model, the level-set transport equation is also modified by adding a source term. The resulting equation is

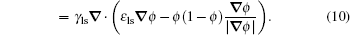
The third term on the left-hand side in Eq. (

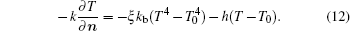
Schematic of laser drilling and corresponding boundary conditions.
With the modified mathematical equation group composed of Eqs. (
Moreover, in the simulation of laser drilling, the laser beam is in the TEM00 mode with a wavelength of 1064 nm and pulse duration of 1 ms. The laser pulse can be written as

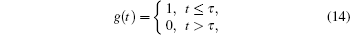
In order to deal with latent heat due to phase transitions, equivalent specific heat capacity method commonly used in fixed grids techniques for phase changes is applied to this proposed simulation model. The equivalent specific heat capacity equation is given as[43]

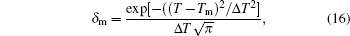
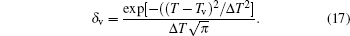
With the modified continuity equation (Eq. (
To enhance the accuracy of calculations, grids of variable spacing were employed consisting of around 51613 elements for the total computational domain of 2.0 mm× 2.0 mm. The grid spacing was finer near the location of the heat source and coarser away from it. The maximum grid spaces were 20 μm. To increase the convergence of the fluid field analysis, time step was about 10−6 s and the setting time was 10−3 s. Calculations were executed on a personal computer with Intel Core i3-3240 CPU 3.40 GHz and 8.00 GB RAM. The total computational time was about 76 h.
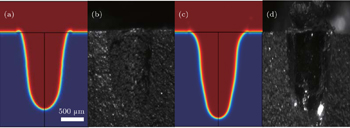
With the above proposed mathematical model, the laser drilling process can be reflected by numerical simulations. Firstly, cross-sections of keyhole for 304 stainless steel (304 SS) and aluminum, measured and calculated via both experiments and simulations, are shown in Fig.
Figure
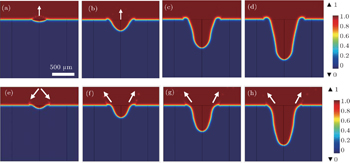
Then, applying the verified simulation model, the melt ejection can be well studied in rather high spatial and temporal resolution. Figure
Figure
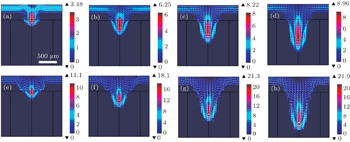
It is worth noting that the ejection speed is not the decisive factor for the quantity of ejected liquid but the thickness of the liquid zone (molten layer) around the keyhole wall is. In order to quantitatively analyze this key point, temperature distributions of 304 SS and aluminum in the drilling process are also obtained in Fig.
The analysis indicates that the difference in liquid zone thickness is mainly caused by thermal diffusivity α which depends on density ρ, specific heat Cp, and thermal conductivity λ, and is given as follows:
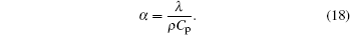
According to Eq. (
In this section, by using the improved mathematical model, the laser drilling process, especially the melt ejection phenomenon, is studied via numerical simulations. Utilizing the calculated flow and temperature field of the keyhole, the relation between the quantity of liquid ejection and material thermal diffusivity is deduced and the conclusions are obtained. Metal material with high thermal diffusivity such as aluminum has a small temperature gradient and thick liquid zone across the keyhole wall, and it is more prone to having a bigger quantity of melt ejection in the laser drilling process. In the following section, experimental observations and measurements are used to verify the conclusions obtained in numerical simulations and analysis.
To verify the numerical simulation and the relation between melt ejection and thermal diffusivity, experiments are conducted for direct observation and measurements. The quasi-real time observations of laser drilling are realized by the shadowgraphic technique. The experimental setup is shown in Fig.
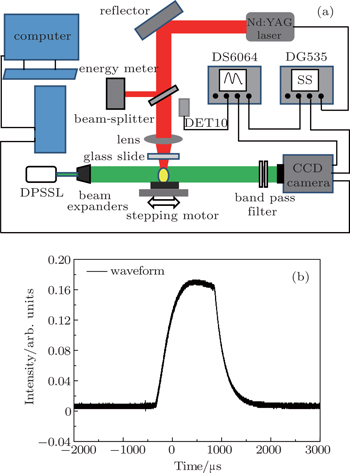 | Fig. 7. (a) Schematic of real time laser drilling observation via the shadowgraphic technique, and (b) the laser pulse waveform with an FWHM of τ being 1 000 μs. |
The shadowgraphs of melt ejection for both 304 SS and aluminum, captured by the real time laser drilling observation system, are shown in Figs.
 | Fig. 9. Optical microscope images of a drilled hole showing material removal from the hole in the melt phase for (a) 304 SS and (b) aluminum. Drilling conditions are the same as those in Fig. |
From this experimental observation and analysis it follows that the melt ejection control is of great importance in keyhole manufacturing (for different materials with widely different thermal properties): it is a significant process in keyhole formation during laser drilling, besides, the spatter is also an important factor for burr, dross and hump formation along the keyhole periphery. Since the surface quality is as important as the formed keyhole structure, understanding the melt ejection in laser drilling is useful for keyhole fabrication and surface quality control.
In order to understand the mechanisms of melt ejection in laser drilling in detail, in this paper, both simulations and experiments are carried out to study the influences of material parameters on melt ejection in laser drilling on 304 SS and aluminum targets. With an improved mathematical model, the result shows that melt ejection is influenced not only by the forces acting on the free surface and fluid flow in the melt pool, but also by the liquid zone (molten layer) across the keyhole wall. According to heat transfer theory, the thickness of the liquid zone is mainly determined by the thermal diffusivity of material. For high thermal diffusivity material like aluminum, a small temperature gradient occurs in the solid target, and a thick liquid zone will be generated across the keyhole wall. These molten metals mainly contribute to melt ejection. Finally, experimental measurements for both 304 SS and aluminum verify the accuracy of the mathematical model and the quantitative analysis for melt ejection. Additionally, the conclusions presented in this paper can be applied to other metals such as copper, nickel based alloys and titanium, etc.
With both proposed numerical simulations and experimental observations, the quasi-quantitative relation between melt ejection and thermal diffusivity is established: materials with high thermal diffusivity, such as aluminum, small temperature gradient and thick liquid zone across the keyhole wall, easily generate a large quantity of melt ejection in a long pulsed laser drilling process. The research in this paper will serve as a guidance for manufacturing optimization and quality control in laser drilling.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 | |
| 47 | |
| 48 | |
| 49 |