Electromagnetically induced transparency (EIT) is an interesting phenomenon which was first observed in atomic vapors.^[1] It allows a transparency window of the weak probe field at the resonant frequency of a three-level system in the presence of a strong pump field, while the transparency window will disappear in the absence of the pump field. EIT is caused by the destructive quantum interference between different pathways of the internal quantum states.^[2] It has led to many unexpected applications, such as the realization of slow light,^[3] vibration cooling,^[4] quantum memory,^[5] frequency transfer,^[6] and normal-mode splitting.^[7]

Recently, EIT has been studied in many novel systems. Some new phenomena were observed, such as, the coupled-cavity-induced transparency appeared in the double-cavity system^[8,9] and the optomechanical induced transparency appeared in the optomechanical system.^[10–13] Double optomechanically induced transparency has also been investigated, which has been achieved in the coupled-disks structure,^[14] charged-resonators optomechanical cavity system,^[15] double-resonators optomechanical system,^[16,17] and couple-cavity optomechanical system.^[18] Furthermore, the multiple-OMIT has been achieved in the atomic-media assisted optomechanical system^[19] and multiple-resonators optomechanical system.^[20] Double- and multiple-OMIT have extend the single EIT to those with double or triple transparency windows, which have led some new applications, such as the all-optical quantum network and multi-channel quantum information processing.^[21]

In this work, we consider a two-cavity optomechanical system, in which the two cavities couple to each other via the common waveguide. A strong pump field is applied to one cavity and a weak probe field is applied to the other. Our results illustrate that with the excitation of the strong pump field, triple-OMIT appears in the spectrum of the output probe field. This optomechanically induced transparency is associated with the coupling between the two cavities, as well as the coupling between the cavities and the mechanical resonators.

Nowadays, the strong coupling between two photonic nanocavities has been observed in the structure based on a two-dimensional photonic crystal,^[22] and the coupling strength can be controlled by tuning the distance between them. Moreover, strong optomechanical coupling between femtogram nanomechanical resonators and high-Q photonic nanocavities has also been realized in the two-dimensional photonic crystal.^[23] Therefore, the two-dimensional photonic crystal is a feasible experimental scheme for our system to be realized.

Different from the other double-resonators optomechanical system which consists of two different resonators in a single cavity,^[16] our model has two identical mechanical resonators, but they lead to different quantum interference pathways. We provide a new approach to produce multi-OMIT in multi-cavities optomechanical systems.

The paper is organized as follows. In Section 2, we introduce the model and the analytical expressions of the two-cavity optomechanical system, and with the standard derivation, we obtain the general analytical expression for the component of the output field at the probe frequency. In Section 3, we present the numerical results for the triple-OMIT, with the parameters chosen based on recent experiments. Then we give a detailed physical explanation for the optical phenomenon and analyze the significant factors of the system. Finally, we give a brief conclusion in Section 4.

The scheme investigated is illustrated in Fig. 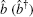1. The two optomechanical cavities a and c are coupled to each other via the common waveguide with a coupling strength J. The mechanical resonator b (d) couples to the cavity a (c) with the coupling strength g_a (g_c) via the radiation pressure. The annihilation (creation) operators for cavities a and c are defined as â (â^†) and ĉ (ĉ^†). Moreover, and are the annihilation (creation) operators of the nanomechanical resonators b and d. The frequencies of the two resonators are ω_b and ω_d. We assume that a strong pump field with frequency ω_pu is applied to the cavity a and a weak probe field with frequency ω_pr is applied to the cavity c.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Schematic diagram of the optomechanical system consisting of two coupled optical cavities a and c, which are connected by a common waveguide. Two mechanical resonators b and d couple to them via the radiation pressure, respectively. The system is driven by a strong pump field and a weak probe field.

The total Hamiltonian of the whole system in the rotating frame at the pump laser frequency ω_pu reads

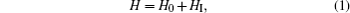
Here, H₀ is the free Hamiltonian of the system. The first two terms describe the free Hamiltonian of the two optical modes, and the last two terms describe the free Hamiltonian of the two mechanical modes. H_I is the interaction Hamiltonian of the system. The first term describes the interaction between the two cavities, the second and the third terms describe the optomechanical interactions in cavities a and c. g_a = (ω_pu/L)x_b and g_c = (ω_pu/L)x_d are the single-photon coupling rates, where and are the zero-point motion of mechanical modes b and d, and m_b and m_d are the masses of the two mechanical resonators. The last three terms describe the input laser Hamiltonian with driving strength and probing strength ,where P_pu denotes the input power of the pump field and P_pr denotes the power of the probe field. κ_a (κ_c) is the decay rate of photons leaving optical cavity a (c) into the associated outgoing modes, and γ_b (γ_d) is the intrinsic mechanical damping rate of resonator b (d).

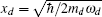
In order to describe the coupling dynamics of the system, we use the formalism of the quantum Langevin equations.^[24] Omitting the hat symbol for simplicity, the Heiserberg–Langevin equations of the intracavity modes and mechanical modes can be written as

In the following, we linearize the operators around the steady-state values by assuming a = 〈a〉_s + δa, c = 〈c〉_s + δc, b = 〈b〉_s + δb, d = 〈d〉_s + δd. We also assume that the fluctuation operators δa, δc, δb, and δd have zero mean. Here 〈a〉_s, 〈c〉_s, 〈b〉_s, and 〈d〉_s are the steady-state values of the system when only the strong driving field is applied, as ɛ_pr ≪ ɛ_pu, they can be obtained from Eqs. (4)–(7) as

Furthermore, ignoring the small nonlinear terms, we can obtain the following linearized quantum Langevin equations:

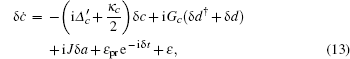
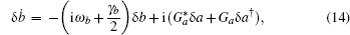
We assume that the cavity is driven by a control field at the mechanical red sideband with and the system is operated in the resolved sideband regime ω_b(d)/κ ≫ 1. The mechanical resonator b (d) has a high quality factor ω_b(d)/γ_m ≫ 1. As a_s and c_s can be obtained by Eqs. (8) and (9), we have

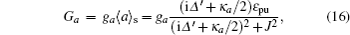
Transforming the equations into the interaction picture by introducing δa → δae^−iδt, δc → δc e^iδt, δb → δbe^−iδt, δd → δd e^−iδt, δɛ → δɛ e^−iδt, δ f → δ fe^−iδt, and ignoring the fast oscillating terms e^2iδt, we obtain the following equations:

By applying the input–output relation of the intracavity field,^[25] which is

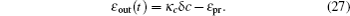
For numerical work, the parameters of the optical cavity and the mechanical resonator we used are based on the realistic cavity optomechanical system.^[26] The coupling strength between the cavities is chosen based on the experimental double-cavity system,^[22] which can reach the strong coupling region, and it can be controlled by adjusting the distance between the cavities.

Triple-OMIT based on the coupled-cavity optomechanical system we considered is illustrated in Fig. 2. The absorption Re[ɛ_T] and dispersion Im[ɛ_T] of the output field are plotted as a function of (δ − ω_b)/ω_b. Three dips of the absorption line correspond to the three transparency frequencies of the probe field. They are determined by the imaginary parts λ_± and real part γ_d/2, which have been given in Eq. (28). Moreover, different from other multiple optomechanically induced transparency systems, which are assisted by atomic media^[19] or composed of many mechanical resonators in a single cavity,^[18] the two mechanical resonators in our scheme are identical.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. (a) The absorption Re[ɛT] and (b) dispersion Im[ɛT] as a function of (δ − ωb)/ωb. The parameters are ga/2π = gb/2π = 910 kHz, κa/2π = κc/2π = 488 MHz, γb/2π = γd/2π = 35 kHz, ωb/2π = ωd/2π = 3.68 GHz, ωa/2π = ωc/2π = 195 THz, ωpu = ωa − ωb, pump power ɛpu = 800ωb, and coupling rate J = 2.5 GHz.

If we ignore the optomechanical coupling G_a and G_c, the term ɛ_T becomes

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. (a) The absorption Re[ɛT] and (b) dispersion Im[ɛT] as a function of (δ − ωb)/ωb without the optomechanical coupling, i.e, ga = gc = 0. (c) The absorption Re[ɛT] and (d) dispersion Im[ɛT] as a function of δ/ωb with the coupling between cavity c and optomechanical resonator d being zero, i.e., gc = 0. The other parameters are the same as those in Fig. 2.

If we only ignore the optomechanical coupling G_c in cavity c, ɛ_T becomes

The origin of the triple-OMIT can be explained by the quantum interference effects, the energy level configuration is presented in Fig. 4. For a coupled two-cavity system, the normal optical mode splits into two modes and the EIT-like window of the output field is established, which is based on the destructive interference.^[8] If the resonator b is coupled to the cavity a via optomechanical interaction, the additional optomechanical coupling will break down the symmetry of the EIT-like level. Then the single transparency window is split into two windows, which induces the occurrence of double OMIT.^[18] Moreover, when the coupling between the resonator d and the cavity c occurs, another pathway of quantum interference forms via the optomechanical interaction, which will lead to another transparency frequency of the probe field with the condition ω_pr − ω_pu ∼ ω_d. As a result, the triple-OMIT occurs, which yields three transparency windows of the probe field. The mechanical resonators b and d are identical, but they lead to different quantum interference pathways.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Energy level structure of the coupled-cavity optomechanical system. The number states of photons and phonons are denoted by ni (i = a,c,b,d). The tunneling coupling strength between |na,nc + 1, nb,nd〉 and |na + 1, nc,nb,nd〉 is J, the coupling strength between |na,nc,nb + 1,nd〉 and |na + 1,nc,nb,nd〉 is Ga, and the coupling strength between |na,nc,nb,nd + 1〉 and |na,nc + 1,nb,nd〉 is Gc.

To further explore the characteristic of the tunable triple-OMIT, we plot the absorption Re[ɛ_T] as a function of (δ − ω_b)/ω_b and ɛ_pu in Fig. 5. According to Eqs. (16) and (17), the optomechanical coupling strengths G_a and G_c are both proportional to the power of the pump field. The parameters κ_a and κ_c we used can be ignored compared to Δ′, and the ratio of the total coupling strength in the two cavities can be obtained as G_a/G_c = Δ′/J, with Δ′ = ω_b. As the parameter we used J (= 2 GHz) < Δ′ (= 3.68 GHz), we have G_a < G_c. In the absence of the driving field, the single transparency window appears, which is induced by the coupling between the cavities.^[8] When a weak pumping field is applied, the coupling strength G_a between resonator b and cavity a is strong enough to break down the symmetry of the EIT-like level, which induces the double OMIT, while the coupling strength G_c between resonator d and cavity c is not strong enough to lead to another pathway of quantum interference. With the increase of the power of the pump field, the coupling strength G_c will gradually become strong enough to induce the appearance of triple-OMIT. The width of the transparency window is proportional to the power of the pump field ɛ_pu, as shown in the inset. It is in accord with Eqs. (24) and (25), which depict the dips of the absorption and the width of the window, respectively, and the similar case has been studied in the atom systems.^[27]

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. The absorption Re[ɛT] as a function of (δ − ωb)/ωb and pumping power ɛpu, where J = 2 GHz, and the other parameters are the same as those in Fig. 2. The inset is the front view.

Figure 6 presents the variation of the absorption Re(ɛ_T) with (δ − ω_b)/ω_b for different coupling strengths between the cavities. In the absence of the coupling between the two cavities, the total optomechanical coupling strength G_c in cavity c is zero. As a result, no interference pathway forms between the pump field and the probe field. With the enhancing of the coupling strength J, the interference strength between the pump field and the probe field is increased, which induces the enlarging of both the transparency depth and the widths of the three windows, and the result also accords with Eqs. (24) and (25).

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. The absorption Re[ɛT] as a function of (δ − ωb)/ωb and coupling strength J, where ɛpu = 800ωb, and the other parameters are the same as those in Fig. 2. The inset is the front view.

For a more general case, we discuss the absorption of the triple-OMIT with two mechanical resonators slightly different in frequency. As illustrated in Fig. 7, compared to those in the ω_d = ω_b case, the absorption curves move rightward (leftward) in the case of ω_d < ω_b (ω_d > ω_b). As the transparency frequency of the probe field is determined by the condition ω_pr − ω_pu ∼ ω_d, when enlarging (diminishing) the frequency of the mechanical resonator d, the transparency of the probe field will move rightward (leftward). The principal frequency of the pumping field in cavities a and c is determined by the condition ω_a − ω_pu ∼ ω_b, with ω_a ∼ ω_c, when ω_d ≠ ω_b, the windows will split into three windows asymmetrically.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. The absorption Re[ɛT] as a function of (δ − ωb)/ωb for identical and different mechanical resonator frequencies: ωd = ωb (black solid line), ωd = 1.1ωb (red dashed line), ωd = 0.9ωb (blue dotted-dashed line). The other parameters are the same as those in Fig. 2.

We have demonstrated the generation of a triple-OMIT for the probe field. The system we considered is a two-cavity optomechanical system, and the two cavities couple to each other via a common waveguide. Based on the quantum interference effects, under the exciting of a strong pump field, three transparency windows of the output field will appear at the probe frequency. It can be analyzed as a combinatorial effect, which is composed of the coupled-cavity-induced transparency effect and the optomechanically induced transparency effect. We also find that the power of the pump field and the coupling strength of the two cavities are two significant factors for the triple-OMIT. The width of the transparency windows is proportional to both of them. Moreover, different from other multiple optomechanically induced transparency systems, the two mechanical resonators in our scheme are identical, and they lead to different quantum interference pathways. Our work provides a new approach to produce multi-OMIT in multi-cavities optomechanical systems.