Cite this Article
Yuan Hong-Chun, Xu Xue-Xiang, Xiao Jin, Xiong Chao, Zhu Xi-Fang. Higher-order nonclassical effects generated by multiple-photon annihilation-then-creation and creation-then-annihilation coherent states. Chinese Physics B, 2016, 25(5): 054202  
Permissions
Higher-order nonclassical effects generated by multiple-photon annihilation-then-creation and creation-then-annihilation coherent states
Yuan Hong-Chun1, 3, †, , Xu Xue-Xiang2, Xiao Jin1, Xiong Chao1, Zhu Xi-Fang1, 3
College of Electrical and Optoelectronic Engineering, Changzhou Institute of Technology, Changzhou 213002, China
College of Physics and Communication Electronics, Jiangxi Normal University, Nanchang 330022, China
Changzhou Institute of Modern Optoelectronic Technology, Changzhou 213002, China

 

† Corresponding author. E-mail: yuanhch@126.com

Project supported by the National Natural Science Foundation of China (Grant Nos. 11447002 and 11447202), the Natural Science Foundation of Jiangxi Province of China (Grant No. 20151BAB202013), and the Research Foundation for Changzhou Institute of Modern Optoelectronic Technology of China (Grant No. CZGY15).

Abstract
Abstract

We explore two observable nonclassical properties of quantum states generated by repeatedly operating annihilation-then-creation (AC) and creation-then-annihilation (CA) on the coherent state, respectively, such as higher-order sub-Poissonian statistics and higher-order squeezing-enhanced effect. The corresponding analytical expressions are derived in detail depending on m. By numerically comparing those quantum properties, it is found that these states above have very different nonclassical properties and nonclassicality is exhibited more strongly after AC operation than after CA operation.

PACS: 42.50.Dv;42.50.–p;03.65.–w;
Keyword:non-Gaussian operation;sub-Poissonian statistics;higher-order squeezing;
1. Introduction

Gaussian states, such as coherent and squeezed states, play an important role in quantum optics and quantum information processing with continuous variables.[1] However, with rapid development in the area of quantum information theory, the de-Gaussification process has attracted much interest in order to overcome the limitations of Guassian light fields. De-Gaussification[2–4] can be realized in a simple manner by adding (subtracting) photons to (from) a Gaussian field and the resulting states are known to exhibit non-classical properties such as sub-Poissonian statistics,[5] higher-order squeezing,[6] antibunching,[7] and negativity of Wigner function.[8] The photon-added coherent state (PACS), first proposed by Agarwal and Tara,[9] was obtained by repeated application of the photon creation operator to the coherent state (CS) and exhibited highly nonclassical properties.[10] Briefly, a photon-added squeezed CS[11] was introduced and its nonclassical properties related to the coherent amplitude were discussed. Nha’s group has recently presented the coherent superposition of photon subtraction and addition,[12] ta + ra†, as well as other coherent superpositions of second-order operations,[13] ta2 + ra†2, for quantum state engineering. Particularly, they performed the coherent superposition on two-mode squeezed vacuum for enhancing quantum entanglement or non-Gaussian entanglement distillation.[14,15] Later, the generalized photon-added CS[16,17] was presented by repeatedly applying a† + a to the coherent state and the generalized photon modulated thermal state[18] was obtained by repeatedly acting ta + ra† on the thermal state.

In another development, much attention has been paid to the sequential operations, such as annihilation-then-creation a†a (AC) and creation-then-annihilation aa† (CA), on a given state. Among them, Yang and Li[19] also analyzed the operation ala†k and its inverse aka†l on an arbitrary state. Wang et al.[20] also investigated the nonclassicality generated by the operation ala†k on the CS. On the other hand, Lee’s group[21] investigated the properties of these states obtained by repeatedly applying (a†a)m and (aa†)m to the CS and thermal state, respectively. Very recently, our group also studied repeatedly applying (a†a)m and (aa†)m to the thermal state[22] and squeezed vacuum state[23] and compared their nonclassical and non-Gaussian properties. However, in Ref. [21], their discussion was restricted to study the single-photon ACCS and the corresponding Mandel Q factor. In the present paper, we focus our study on the higher-order nonclassical effects of two kinds of quantum states, denoted by MPACCS and MPCACS, generated by operating (a†a)m and (aa†)m on the CS, respectively. Due to the noncommutativity between creation and annihilation operator, these states generated by AC operation and CA operation have clearly different nonclassical properties. We first derive the analytical expressions of normalization factors, mean photon number, and photon number distribution (PND) of MPACCS and MPCACS, respectively. Next, two observable nonclassical properties are explored and numerically compared in terms of higher-order sub-Poissonian statistics and squeezing-enhanced effect. Particularly, we investigate how AC and CA operations affect those nonclassical properties. It is shown that their nonclassicality is exhibited more strongly after AC operation than after CA operation.

2. MPACCS and MPACCS

To begin with, let us introduce multiple-photon annihilation-then-creation coherent state (MPACCS) and multiple-photon creation-then-annihilation coherent state (MPCACS). Theoretically, MPACCS is obtained by repeated application of a†a to the coherent state, i.e.,

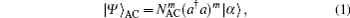
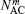
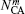
where denotes the normalization constants to be determined, m may be any non-negative integer, |α〉 = exp(−|α|2/2 + αa†)|0〉 and a†,a are the creation and annihilation operation, respectively, obeying [a,a†] = 1. Similarly, by repeatedly operating aa† to the coherent state |α〉, one can generate another non-Gaussian state, i.e., MPCACS,

where is also the normalization constant. As mentioned below, |Ψ〉AC and |Ψ〉CA exhibit entirely different nonclassicality due to [a,a†] = 1.

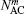
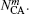
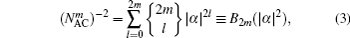
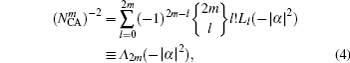
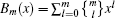
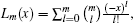
To fully describe two kinds of quantum states, we want to calculate the normalization constant and Noting the operator identities (see Eqs. (A5) and (A8) in Appendix A), we have

and

where is just the Bell-polynomial,[24] and we have considered 〈α|ama†m|α〉 = m!Lm(−|α|2) with the Laguerre polynomial which is just the normalization constants of PACS.

We see from Eqs. (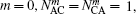3) and (4) that their normalization factors are different due to the noncommutativity. In particular, for the case of no-photon-operation with and both |Ψ〉AC and |Ψ〉CA reduce to coherent state as expected. For m = 1, and as expected. Since the normalization factors of the MPACCS and MPCACS are related to the Bell polynomial and the Laguerre polynomial, respectively, it is very convenient for further analytically studying and comparing their nonclassical properties of the states generated by AC and CA operations.

For instance, according to 〈n〉 = Tr(a†aρ), from Eqs. (3) and (4) we easily have mean photon numbers of MPACCS and MPCACS, respectively,

and

By using Eqs. (1) and (A5) and considering and a†a|n〉 = n|n〉, the probability of finding n photons in |Ψ〉AC is given by

which is just photon number distribution (PND) of MPACCS. Similarly, using Eqs. (2) and (A8) we also have the PND of MPCACS

For the especial case, when becomes Poisson distribution, which is just the PND of CS.

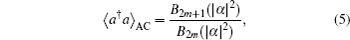
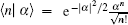
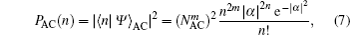
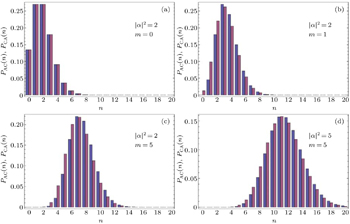
According to Eqs. (7) and (8), in Fig. 1 we plot the PNDs of MPACCS and MPACCS in the same bar graph versus n for several different values of |α|2 and m. It is apparent from the plots that the positions of peaks of PAC(n) and PCA(n) depend on m and the value of coherent state initially. By increasing the number of photon-operation, we are able to move the peak along the increasing photon number (see Figs. 1(a)–1(c)). In addition, when m = 0, PAC(n) is the same as PCA(n) in Fig. 1(a), which just describes the PND of CS. For m ≠ 0, AC operation has a larger PND than CA operation before reaching the peak position, conversely after the peak position AC operation has a smaller PND than CA operation (see Figs. 1(b)–1(d)).

Fig. 1. PND of the states |Ψ〉AC ((a), (c)) and |Ψ〉CA ((b), (d)) versus n for several different values of |α|2 and m.
3. Higher-order sub-Poissonian statistics

The sub-Poissonian statistics is a key characteristic of every optical field. We now examine the higher-order sub-Poissonian statistics of MPACCS and MPCACS in terms of factorial moment, which is defined by[25,26]

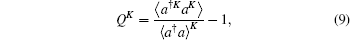
where K is a positive integer. For all K ≥ 2, QK = 0 corresponds to the Poisson distribution. The negative or positive values of QK parameter K > 2 indicates higher-order sub-Poissonian or higher-order super-Poissonian statistics. In fact, this class includes the case of K = 2 related to Mandel Q parameter as QK = 2 = Q/〈a†a〉. Similarly, the negativity of Q parameter refers to sub-Poissonian statistics. All Fock states result in Q = −1, and all coherent states have Q = 0.

For the MPACCS, using Eqs. (1) and (A5), we directly calculate

where we have set and used the integral formula[27]

with Hm,n(η,ξ) being the two-variable Hermite polynomial. However, in the MPCACS, using Eqs. (2) and (A8), 〈a†paq〉CA is given by

From Eqs. (10) and (12), we easily obtain the results of 〈a†2a2〉AC and 〈a†2a2〉CA when p = q = 2. Substituting it into Eq. (9) yields the QK parameters of MPACCS and MPCACS (as shown in Fig. 2), respectively. In particular, when m = 0, QK = 0 is the Poisson distribution, which is just the case of CS. For K = 2, noticing that a†2a2 = (a†a)2 − a†a = (aa†)2 − 3aa† + 2, we simplify

and

According to the definition of Mandel’s Q parameter,[28] we have

and

respectively.

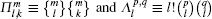
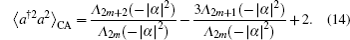
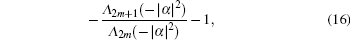
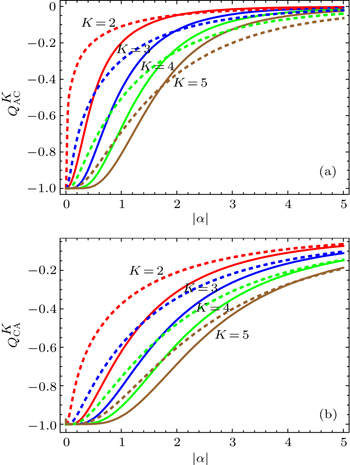Fig. 2. Parameter QK of (a) |Ψ〉AC and (b) |Ψ〉CA as a function of |α| with m = 1 (solid line) and m = 5 (dashed line) for different values of K = 2,3,4,5, respectively.

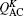
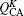
In Fig. 2, we display the dependence of parameter QK as a function of |α| for different values of K in MPACCS and MPCACS and in Fig. 3 we also depict their parameters Q as a function of |α| for different values of m. For α ≠ 0,m ≠ 0, the value of QK is negative for all |α| and m, which absolutely exhibits a significant amount of higher-order sub-Poissonian statistics. For a given |α|, and become more and more negative with the increase of K. This indicates that the higher-order sub-Poissonian character (K = 3,4,5) is more pronounced than the usual sub-Poissonian behavior (K = 2) and the degree of higher-order sub-Poissonian behavior becomes bigger with the increase of K. For the small values of |α|, the increasing m may produce stronger higher-order sub-Poissonian statistics (such as m = 1 and m = 5 in Fig. 2). Comparing Figs. 2(a) and 2(b) (or Fig. 3) shows that MPACCS exhibits slightly stronger nonclassicality than MPCACS.

Fig. 3. Parameter Q of |Ψ〉AC and |Ψ〉CA as a function of |α| for different values of m = 1,2,3,4, respectively.
4. Higher-order squeezing-enhanced effect

As another example of the nonclassical effect, we explore how the squeezing quantitatively changes when AC and CA operations act on the coherent state. For this purpose, we consider the quadrature operator Xθ = aN e−iθ + a†N eiθ, and the squeezing is characterized by the minimum value[29] 〈:Δ2Xθ: 〉min < 0 with respect to θ, where : : denotes normal ordering, ΔO = O − 〈O〉 represents a quantum fluctuation, and θ is a phase angle. Upon expanding the terms of 〈: (ΔXθ) : 〉, one proposed the optimized nonclassical depth of squeezing Smin over the whole phases, which is given by[30]

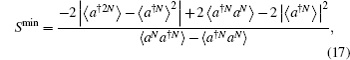
and its negative value only in the range [−1,0) exhibits higher-order squeezing (or nonclassicality). The ideal squeezing corresponds to Smin = 1. N is the order of squeezing, and N = 1 is the case of quadrature squeezing,[31] and N = 2 corresponds to amplitude-squared squeezing.[32] Note that Smin < 0 is also only a sufficient condition for the state to be nonclassical, not a necessary one.

In a similar way to derive Eqs. (10) and (12), we finally get

and

where in the last equation we have used In addition, for the term 〈a†NaN〉 in Eq. (17), it is obtained from Eqs. (10) and (12) in a straightforward manner, namely, p = q = N. Thus, based on Eq. (17), the nonclassical depth of squeezing Smin of MPACCS and MPCACS changing with |α| for several different N and m is depicted in Fig. 4. The squeezing occurs only when |α| is big enough, and in the limit of the big values of |α|, Smin tends to be zero and the squeezing disappears. It is clearly shown from Fig. 4 that the degree of squeezing at a fixed m becomes smaller when N increases, whereas the degree of squeezing for a given N increases with increasing m. In addition, we get more squeezing after AC operation than after CA operation when |α| is big enough. These indicate that the MPACCS and MPCACS exhibit higher-order squeezing-enhanced effect.

Fig. 4. (colour online) Squeezing depth Smin of |Ψ〉AC (solid lines) and |Ψ〉CA (dashed lines) as a function of |α| for different values of (a) N = 1,2,4 with m = 2 and (b) m = 1,2,4 with N = 2, respectively.
5. Conclusions

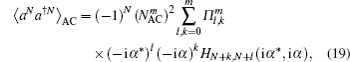
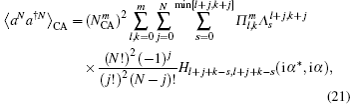
In summary, we introduce two kinds of quantum state (MPACCS and MPCACS) by repeatedly operating AC and CA operation on the CS and then numerically investigate their higher-order nonclassicality. Their normalization factors are analytically derived in compact expressions, where the former turns out to be the Bell-polynomial and the latter is related to Laguerre polynomial. Based on this, we also obtain mean photon number and photon number distribution of MPACCS and MPCACS, respectively. Furthermore, we shall explore their observable higher-order nonclassical properties such as higher-order sub-Poissonian statistics and higher-order squeezing-enhanced effect, which exhibits their highly nonclassical behaviors depending on m. By comparing their quantum characters, we conclude that the nonclassical states generated by AC operation can present stronger nonclassicality than those generated by CA operation.

Reference
1Dodonov V V 2002 J. Opt. B: Quantum Semiclass. Opt. 4 R1
2Hu L YXu X XWang Z SXu X F 2010 Phys. Rev. 82 043842
3Meng X GWang ZFan H YWang J S 2012 J. Opt. Soc. Am. 29 3141
4Wang ZLi H MYuan H C 2014 J. Opt. Soc. Am. 31 2163
5Short RMandel L 1983 Phys. Rev. Lett. 51 384
6Hong C KMandel L 1985 Phys. Rev. Lett. 54 323
7Kimble H JDagenais MMandel L 1977 Phys. Rev. Lett. 39 691
8Hillery MO’Connell R FScully M OWigner E P 1984 Phys. Rep. 106 121
9Agarwal G STara K 1991 Phys. Rev. 43 492
10Duc T MNoh J 2008 Opt. Commun. 281 2842
11Xin Z ZDuan Y BZhang H MHirayama MMatumoto K 1996 J. Phys. 29 4493
12Lee S YNha H 2010 Phys. Rev. 82 053812
13Lee S YNha H 2012 Phys. Rev. 85 043816
14Lee S YJi S WKim JNha H 2011 Phys. Rev. 84 012302
15Ji S WLee S YNha H 2012 Phys. Rev. 85 013839
16Yuan H CXu X XFan H Y 2010 Chin. Phys. 19 104205
17Li H MXu X F 2012 Chin. Phys. 21 024202
18Xu X XYuan H CHu L YFan H Y 2011 J. Phys. A: Math. Theor. 44 445306
19Yang YLi F L 2009 J. Opt. Soc. Am. 26 830
20Wang ZYuan H CFan H Y 2011 J. Opt. Soc. Am. 28 1964
21Lee S YPark JJi S WOoi C H RLee H W 2009 J. Opt. Soc. Am. 26 1532
22Xu X XYuan H CWang Y 2014 Chin. Phys. 23 070301
23Xu X XYuan H CZhou L 2015 Opt. Commun. 335 133
24Riordan J1980An Introduction to Combinatorial AnalysisPrincetonPrinceton University Press
25Lee C T 1990 Phys. Rev. 41 1721
26Agarwal G STara K 1992 Phys. Rev. 46 485
27Li H MYuan H C 2010 Int. J Theor. Phys. 49 2121
28Mandel LWolf E1995Optical Coherence and Quantum OpticsLondonCambridge University Press
29Hong C KMandel L 1985 Phys. Rev. 32 974
30Lee JKim JNha H 2009 J. Opt. Soc. Am. 26 1363
31Loudon RKnight P L 1987 J. Mod. Opt. 34 709
32Hillery M 1987 Phys. Rev. 36 3796
33Fan H YLu Y L 2012 Front. Phys. 7 261
34Rennie B CDobson A J 1969 J. Combinatorial Theor. 7 116
35Fan H Y 2003 J. Opt. B: Quantum Semiclass. Opt. 5 R147