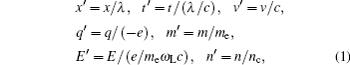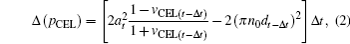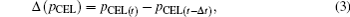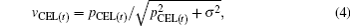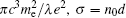School of Science, Shanghai Institute of Technology, Shanghai 201418, China
† Corresponding author. E-mail: fcwang@sit.edu.cn
Project supported by the Shanghai Provincial Special Foundation for Outstanding Young Teachers in University, China (Grant No. yyy10043).
1. IntroductionThe laser intensities up to the order of 1022 W/cm2 can now be obtained in the experiments with the development of the laser technology.[1,2] High-energy ions can be accelerated by the intense laser plasma interaction, which can be applied in fast ignition for initial confinement fusion,[3,4] medical therapy,[5,6] proton imaging,[7] etc. Generally, radiation pressure acceleration (RPA)[8–26] may be used to get a mono-energetic ion beam, because the ponderomotive force is stable. There are two electric field peaks due to the two components of the ponderomotive force of the linearly polarized (LP) laser. One is the non-oscillating part −(e2/4meω2)∇E2(x), and the other is the oscillating part −(e2/4meω2)[cos(2ω0t)]∇E2(x), where e is the electron charge, me is the electron mass, ω0 is the laser frequency, and E is the laser electric field. However, the detail dynamics of the oscillating part of the ponderomotive force is not clear. How to reduce the oscillating force and improve the proton acceleration by the linearly polarized pulse should be considered.
Previously, a quasi-equilibrium on the compressed electron layer (CEL) has been investigated.[12] Two balance conditions were studied. One is the balance between the laser pressure and the electrostatic charge-separation field forces,[10,12] aL(1 + η)1/2 ≈ (n0/nc)(l0/λ), where η is the reflecting efficiency,  is the critical density, λ is the laser wavelength and n0 and l0 are the initial foil density and thickness, respectively. The other condition is the phase stable acceleration (PSA),[12] aL < (n0/nc)(2πl0/λ). These two conditions give static solutions at the end of the hole-boring stage neglecting the effects of the ion motion.
is the critical density, λ is the laser wavelength and n0 and l0 are the initial foil density and thickness, respectively. The other condition is the phase stable acceleration (PSA),[12] aL < (n0/nc)(2πl0/λ). These two conditions give static solutions at the end of the hole-boring stage neglecting the effects of the ion motion.
In this paper, the dynamic of the proton acceleration by a linearly polarized laser is investigated. Dynamics of the CEL is studied both by a one-dimensional (1D) dynamic model and particle-in-cell (PIC) simulations. It is found that the CEL disperses in a few cycles of the laser duration, because the CEL comes back with a large velocity in the opposite direction of the laser. A larger wavelength laser can be used to reduce the turbulence of the CEL to a certain extent to get the more stable proton acceleration. The proton acceleration driven by the LP laser is very important under the present laboratory conditions. Surely, the CP laser can produce the proton beam with mono-energetic spectra. However, it requires critic experimental conditions, such as high laser intensity, high laser contrast, and super thin foil. In fact, the LP laser can be more easily generated compared with the CP laser. The LP laser may be efficient for the practical experiments if the spectrum of the proton beam is not required to be super mono-energetic.
2. Theoretical analysisThe 1D dynamic model of the CEL is shown in Fig. 1. The incident laser pulse is totally reflected, corresponding to η = 1. A dense compressed electron layer is built up when the laser pulse illuminates the foil. The maximum electrostatic charge-separation field is E0 = 4πen0d for the case of fixed ions. The total electrostatic force on the CEL is  where the density conservation relationship is np0(l − d) = n0d.[10] Here l − d(l < l0) is the temporal thickness of the CEL. The incident laser pressure in the instantaneous frame of the foil is (2I/c)(c − vCEL)/(c + vCEL), where vCEL is the velocity of the CEL surface. Then CEL dynamics is obtained by analyzing the total electrostatic force and the laser pressure force. Here we use the model of sharp-front laser interaction, where the ions cannot catch up the CEL during the hole-boring stage. In general, the instabilities can be reduced to a certain extent by using the sharp-front laser.
where the density conservation relationship is np0(l − d) = n0d.[10] Here l − d(l < l0) is the temporal thickness of the CEL. The incident laser pressure in the instantaneous frame of the foil is (2I/c)(c − vCEL)/(c + vCEL), where vCEL is the velocity of the CEL surface. Then CEL dynamics is obtained by analyzing the total electrostatic force and the laser pressure force. Here we use the model of sharp-front laser interaction, where the ions cannot catch up the CEL during the hole-boring stage. In general, the instabilities can be reduced to a certain extent by using the sharp-front laser.
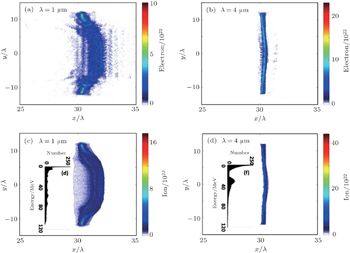
In this paper, the variables are normalized as
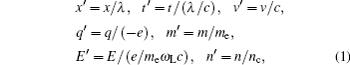
where
x,
t,
v,
q,
m,
E, and
n are the length, time, velocity, charge, mass, field, and density, respectively. To be concise, the prime of the normalized variable is omitted. Then the relativistic equations of the CEL dynamics are obtained as
[27,28]
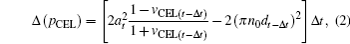
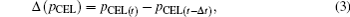
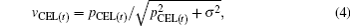

where
pCEL =
σγvCEL is the areal momentum of the CEL normalized by
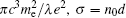
is the areal density of the foil, and Δ
t is the time step. The amplitude of the incident laser pulse at the CEL surface (
x =
dt−Δt) is
at = (
a0/
tup)(
t −
dt−Δt) for
t −
dt−Δt <
tup and
at =
a0 for
t −
dt−Δt ≥
tup. The shape of the laser pulse can be changed with the form of
at. The first term on the right-hand side of Eq. (
2) is the laser pressure and the second term is the electrostatic force.
Then the dynamics of the CEL driven by the linearly polarized pulse can be obtained by Eqs. (2)–(5). Figure 2 shows the velocity of the CEL (ve), laser pressure, and laser intensity a on the surface of the CEL at different times. The laser pulse is linearly polarized. The laser intensity linearly rises up to a = 50 within 1T, remains constant a = 50 for 8T, then linearly decreases to 0 within 1T. Here T = λ/c is the laser period and λ = 1 μm is the wavelength of the laser. The density of the foil n = 40nc. The thickness of the foil is 0.8 μm.
From Fig. 2, it can be found that the interaction begins at t = 50T. The velocity of the CEL ve increases with the increase of laser intensity a, which means that the CEL is accelerated. Such acceleration is driven by the laser pressure, as shown in Fig. 2. Then the laser intensity decreases at about t = 50.5T, which is due to the oscillation of the LP pulse. The laser pressure also decreases at the same time. The CEL is dragged back by the charge-separation field, leading to the decrease of the velocity of the CEL. We can find that the velocity decreases so fast, and ve ∼ −0.8c is obtained at about t = 50.6T. At the same time, the electric field of the laser changes from positive to negative, and the laser pressure increases again. However, the CEL travels in the opposite direction of the incident laser pulse, which may enlarge the laser amplitude on the surface of the CEL by a factor of (1 − vCEL)/(1 + vCEL). For the CEL velocity ve ∼ −0.8c, the laser intensity on the CEL is enlarged to 9at. The corresponding laser pressure is enlarged by a factor of 81. The huge laser pressure pushes the CEL to the velocity of 0.5c within 0.1T (see Fig. 2), which may produce the remarkable turbulence of the CEL.
3. Simulations and discussionThe model of Eqs. (2)–(5) is compared with 1D PIC simulations. A LP laser pulse with a linearly rise-up front (duration 1T) irradiates the target. As the laser amplitude rises up to a = 50, a flat-top amplitude is maintained. Then the intensity linearly decreases to 0 within 1T. The foil is located in the region x = 50λ–50.8λ. The foil is assumed to be fully ionized to electrons and protons, and the foil density is n = 40nc. The length of the simulation box size is 100λ. The numbers of the spatial grids and the particles are 2×104 and 2×106, respectively. To clearly and simply compare the results from the model and the simulation, the ions are fixed firstly, which is reasonable due to the fact that the ions cannot catch the CEL until the ions reach the back side of the target in our case.
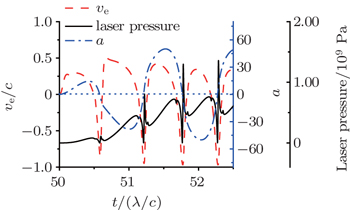
Figure 3 shows the 1D simulation results. It is found that the electrons remain in the compressed layer for the first half cycle of the laser duration (t ∼ 50T–50.5T). The CEL begins to disperse at about t = 50.6T (see Fig. 3(a)), mainly because of the laser pressure acceleration of the coming back CEL. The velocity of the CEL can reach −0.86c, which is almost consistent with the theoretical result in Fig. 2. The huge change of the laser pressure on the CEL will lead to the remarkable turbulence of the CEL, which is also consistent with the theoretical results in Fig. 2. The dispersion of the CEL will become serious as the time goes on when more burger changes of the laser pressure appear. The theoretical model fails when the CEL totally disperses, as shown in Fig. 3(a). Both the theoretical results in Fig. 2 and the simulation results in Fig. 3 show that the oscillating part of the laser pressure of the LP laser produces the dispersion of the CEL, which is bad for the spectra of the laser-driven proton acceleration.
Two-dimensional simulations are used to confirm the predictions from the theoretical model and the 1D simulations. The laser peak amplitude is a = 50. The duration of the pulse is the same as that of the 1D case in Fig. 3. The transverse shape of the laser is four-order super Gaussian, and the size of the focal spot is 10 μm. The foil density is n = 40nc. The foil is located in the region of x = 30 μm–30.5 μm and y = −14 μm–14 μm. The size of the simulating box is 60 μm×60 μm. There are 8000 cells in the x direction and 4800 cells in the y direction. There are 10 macro particles in each cell. The foils are assumed to be fully ionized to protons and electrons before the interaction with the laser pulse in the simulation.
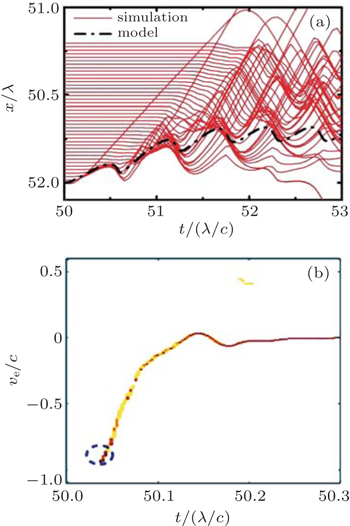
The density distributions of electrons and protons driven by the 1-μm wavelength laser are shown in Figs. 4(a) and 4(c). It can be found that the electrons have dispersed at t = 40T, which has been predicted by the model (see Fig. 2) and the 1D simulation (see Fig. 3). In this case the protons cannot be stably accelerated during the acceleration progress. Figure 4(c) shows that the proton beam also disperses at t = 40T. The corresponding spectrum is broadened and there is no mono-energetic proton beam generated.
The density distributions of electrons and protons driven by the 4-μm wavelength laser are shown in Figs. 4(b) and 4(e). It is found that a larger wavelength of the laser can produce a more stable electron and proton layer. The electron disturbance is much reduced in the case of λ = 4 μm, while the proton energy decreases. The main reason is that a shorter wavelength means more serious instability (see Fig. 3(b)) of electrons, leading to the much greater decrease of the electron temperature. However, an obvious quasi-mono energetic peak appears in the spectrum for λ = 4 μm. Such quasi-mono energetic proton beam is needed for the medical therapy, or the special dealing of proton imaging.
4. ConclusionThe dynamic of the proton acceleration by the LP laser is investigated. Dynamics of the CEL are studied by a simple model, 1D and 2D PIC simulations. It is found that the compressed layer disperses in a few cycles of the laser duration. The CEL comes back with a large velocity in the opposite direction of the laser incident. A larger wavelength laser may be used to reduce the turbulence of the CEL to a certain extent to obtain more stable proton acceleration by modulating the spectra of the proton beam.