Cold atomic physics has achieved great success in the last 30 years. It is hoped that this idea will be extended to molecules,^[1] to improve precision measurements and study novel physics.^[2] The quest to create cold molecules has been ongoing for over 20 years. Electric fields,^[3,4] magnetic fields,^[5,6] and optical fields^[7,8] have been used to slow molecules. However, for all of these methods, the potentials are conservative, so you can slow the molecules, but you cannot increase the phase space density of molecules. Due to this weakness, molecules can only be slowed to mK temperatures, and have a relatively low phase space density.^[1] In the last few years, a new method, laser cooling of polar molecules, has been proposed^[9,10] and realized in experiments with SrF,^[11] YO,^[12] and CaF.^[13] The scattered photons carry out the entropy, so the total entropy of the system can be reduced and the phase space density can increase. Compared with atoms, laser cooling of polar molecules requires more lasers and sophisticated energy level selections. The complicated energy levels of molecules make the laser cooling and trapping of molecules more challenging.

In the atomic case, the magneto-optical trap (MOT) is the starting point for most cold atom experiments, since an MOT can cool and trap a significant number of atoms. Extending this capability to polar molecules is a long-sought goal in the field. After realizing laser cooling of polar molecules,^[11] the Yale group realized a three-dimensional (3D) MOT by using a traditional MOT scheme.^[14,15] A few hundred molecules are trapped and cooled down to around 1 mK, but the spring constant of the MOT force is much weaker than expected. The multi-level model calculation showed that the distribution of molecular populations approaches a “balanced state”, and makes the MOT force very weak.^[16] One way to overcome this problem is switching the MOT.^[12] By quickly switching both the magnetic field and the laser polarization, the populations in each state continuously evolve and the force is not balanced, so a high trapping force can be achieved.

Another progress came from JILA, where the laser cooling of polar molecules was extended to molecules with more intermediate states.^[17,18] For the YO molecule, the Δ state lies lower in energy than the ²Π_1/2 state, and the molecule can decay to the Δ state, then decay back to the ground state. Because of the three-photon decay, the parity of molecules changes when they go back to the ground state. Hence, they decay back to N = 0 and N = 2 states, and they are dark states. In order to close the rotational state transition, two microwaves are added to remix all N = 0, 1, 2 states. This Δ state leakage also happens for other molecules, such as BaF. In JILA’s work, microwaves are used to plug the leakage of the Δ state, and demonstrate the slowing of molecules. Inspired by this work, we further extend this idea to trapping and cooling, and propose to use a microwave-mediatedMOT (μ-MOT), which uses the microwaves to remix the lower states, making the MOT force maintain a high level.

In order to gain some insights into the challenges of making a molecular MOT, one needs to look closely at the molecular energy levels. Here we take BaF as an example, as shown in Fig. 1(a). The main cooling laser connects to the transition X²Σ to A²Π, and sidebands are induced to cover the hyperfine sub-states. A Δ state lies lower in energy than the A²Π state, and molecules can decay through the Δ state to the ground state with rotational numbers N = 0 and N = 2. Two microwaves are introduced to remix these dark states.^[17]

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. (a) Energy structure involved in the laser cooling of BaF. The Δ state leakage means N = 0 and N = 2 should be included in the cycling transition. (b) The simplified 7-level model of μ-MOT. The upper states are nearly degenerate, while the lower states have regular Zeeman splittings, and are coupled with each other through the microwave state |7〉.

Figure 1(a) shows two main features that limit the operation of the molecular MOT.^[16] One is the number of Zeeman states. For traditional MOTs with alkali atoms, we usually operate with F_u > F_l, where F_u and F_l are the angular momentum numbers of the upper and lower states, so there are cycling transitions such as m_F → m_F+1 or m_F → m_F − 1. This was called “Type-I” MOT. For the molecule case, F_u ≤ F_l is the more typical scenario, and we call it “Type-II” MOT. As shown in Fig. 1(a), for BaF, F_u = 0,1 and F_l = 0,1,2, so there will be dark states. For example, if σ + light is used to pump F_l = 1 to F_u = 1, then the m_F = 1 state is a dark state. Once molecules are pumped to the dark states, they no longer interact with the light. Another issue is the small Zeeman splitting of the upper states. Up to now, the molecules that can be cooled all associate with the transition of X²Σ⁺ to A²Π_1/2. Because the spin and orbital angular momenta are nearly equal, but have opposite signs for the A²Π_1/2 state, the total magnetic moments are very close to zero, which means that the effective g-factors for the A²Π_1/2 state are usually small. For example, it is –0.088 for SrF and –0.065 for YO. BaF has a relatively high value, –0.199. The small g factor of the upper state makes the MOT beams balance the force with each other, and results in a small MOT force.

Our proposal to solve these problems is to use a μ-MOT. Physically, microwaves couple the lower states, remix the populations, and break the dark state. In order to reach a sufficient repopulation, the microwave coupling Rabi frequencies should be larger than the upper state decay rate (Ω > Γ).

We numerically analyze a simple one-dimension (1D) case. Figure 1(b) shows the simplified 7-level model. It captures the main features of molecular MOT. The upper states |1,2,3〉 have a small g factor. The lower states |4〉, |5〉, and |6〉 have a normal Zeeman splitting with g_l = 1. The upper states and the lower states are coupled by the cooling laser with σ+ and σ− polarization in one dimension. The state |7〉 can couple to |4〉, |5〉, and |6〉 with microwaves. In order to simplify the calculation, we assume that the Rabi frequencies of the microwave coupling from |7〉 to |4〉, |5〉, and |6〉 are the same,

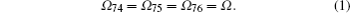
In order to perform numerical calculation, we need to assume that some branching ratios of the upper state decay, as shown in Fig. 2. Because molecules have very complex molecule energy levels, the branching rules for atoms do not apply for molecules. Here, we assume the branching ratio from |2〉 (m = 0) to |5〉 (m = 0) is not zero. Variation of the branching ratios will change the exact numerical results slightly, but the main conclusions are still valid.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. The branching ratios of the 7-level model. Here we make the simple assumption that the branching ratios are equal to every possible decay channel. At the same time, because of the complex energy structure of molecules, we assume that the branching ratio from |2〉 (m = 0) to |5〉 (m = 0) is 1/3.

With this model, we obtain the rate equations,

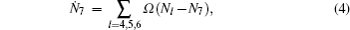
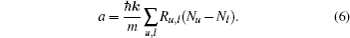
If no microwaves are added, we gain a traditional MOT scheme. In Fig. 3(a), we calculate the population evolutions at position x₀, with μ_BB(x₀) = −5 MHz for zero velocity molecules. The lower states are initially equally populated, then they reach a steady state quickly. At this steady state the trap force is zero, which is a balanced state. The molecules accumulate in |6〉 as shown in Fig. 3(a), because at position x₀, the transition from |6〉 to |2〉 is detuned more. In Fig. 3(b), we plot the associated trapping force. It decays quickly with a decay rate ∼Γ.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. The evolution of (a) the populations and (b) the corresponding force without microwaves. The populations quickly reach a steady state, at which the force is balanced for two counterpropagating beams. Both decay time constants are determined by Γ.

When the microwaves are applied, the MOT force changes. In Fig. 4, we plot the MOT force for both trapping and cooling with different microwave power (Ω = 2π × {0, 0.02, 0.1, 1, 5, 20} MHz). A clear enhancement of theMOT force is evident even when the microwave coupling is small. This is easy to understand: as the microwaves remix the population, the force is not balanced any more, thus the MOT force persists.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. The μ-MOT force for 1D geometry. (a) The trapping force. (b) The cooling force. From bottom to top, the microwave coupling power are Ω = 2π × {0, 0.001, 0.01, 0.1, 1, 10} MHz ({black, red, green, deep blue, dark blue, pink}), respectively.

We can also see that, once Ω reaches a certain value, the MOT force saturates. Physically, the population of each state involved in the microwave coupling becomes the same. In order to study this saturation, we can plot the maximum force versus the microwave Rabi frequency Ω. As shown in Fig. 5, the dramatic change happens from 0.1Γ to Γ. Once Ω approaches Γ, the MOT force saturates. For most molecules, Γ is about a few MHz. Because polar molecules usually have large dipole moments, it is easy for Ω to reach a few MHz experimentally. Here we evaluate the typical value of the microwave coupling strength. For a 1 mW/cm² microwave with an effective dipole moment of 1 Debye, the Rabi frequency is

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. The maximum trapping force versus the microwave Rabi frequency Ω. Even when Ω is much smaller than Γ, huge effects show up. When Ω is comparable with Γ, the trapping force saturates.

Here we compare the μ-MOT with the switching MOT. The switching MOT was used to deal with the “Type-II” MOT structure, and was first realized with molecules in two dimensions,^[12] then extended to the three-diminsional (3D) case.^[19] Using the rate equation, we can calculate the population evolution and thus the force evolution. Figure 6(a) shows the time sequence used in our calculation. The B field and the laser polarizations are switched at the same time with the same phase. We assume that the switching time is much smaller than 1/Γ, so it is non-adiabatic. To get a large MOT force, the period of the switching should be on the same order of the upper state decay time. We choose τ = 1.0 μs, and calculate the MOT force at position x₀. As we can see from Fig. 6(b), the MOT force is the largest at the beginning of each cycle, and then decay exponentially. Every time after switching, the MOT force revives, and the MOT persists. Note that the force curve in Fig. 6(b) is not symmetric for different phases, because at position x₀, the detunings are asymmetric for different phases.

Fig. 6.

Figure Option ViewDownloadNew Window

Fig. 6. (a) The switching sequence used in our calculation. Both the B field and laser polarizations are switched every 1 μs with the same phase. We assume that the switching speed is fast enough. (b) The corresponding force in the switching scheme. The force reaches the maximum value at each cycle. Then the laser coupling makes the populations evolve towards the balanced state, the force decays and is revived again in the next period.

We can average the force to plot the B field and velocity-dependent forces. We plot them together with μ-MOT in Fig. 7. As we can see, the μ-MOT can enhance the MOT force significantly compared with the normal MOT scheme, and recover 60%–70% of the force of the switching MOT. One may naively think that because of averaging, the MOT force of switchingMOT is about half of the bestMOT force. For the μ-MOT, the distribution of the populations at saturation becomes equal. They are not optimized for the largest MOT force, and it is attenuated by the number of states. Hence, the μ-MOT force is lower than the switching MOT force.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. Comparison of the normal MOT, the μ-MOT, and the switching MOT. (a) The trapping force. (b) The cooling force. The normal MOT does not work, since the trapping force is zero. The switching MOT has large trapping and cooling forces. The μ-MOT (Ω = 2π × 20 MHz) has a slightly reduced force.

In conclusion, we have proposed a new scheme for realizing a microwave-mediated molecular MOT. We use a 7-level model to model a 1D system and show that the scheme leads to good MOT operation. The advantage of this scheme is its simplicity. For some molecules like YO and BaF, microwaves are already introduced for laser cooling and slowing. The only additional thing that needs to be done is to broaden the microwaves. Compared with the switching MOT, the μ-MOT has a slightly smaller MOT force, but due to the simplicity, should find applications as a suitable technique for cooling and trapping polar molecules.