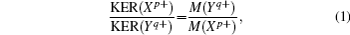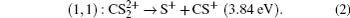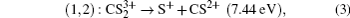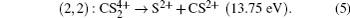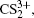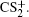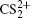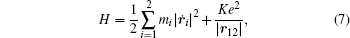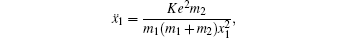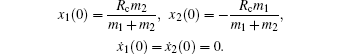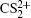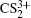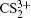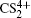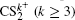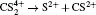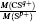1. IntroductionWith the dramatic development of ultrashort laser technique in the past few decades, the ultrashort intense laser field has brought out some unprecedented physical phenomena, such as multi-photon ionization (MPI),[1–3] enhanced ionization (EI) or charge-resonance enhanced ionization (CERI),[4–9] above-threshold ionization (ATI),[10] dissociative ionization,[11–14] Coulomb explosion (CE),[15–23] and so on. As is well known, when the laser intensity is up to 1014 W/cm2, the laser field magnitude is comparable to the Coulomb field generated by an atomic nucleus, the molecular geometry structure can be modified, and thus the molecular chemical bond will be broken by the strong Coulomb repulsive force. Several experimental results indicated that the chemical bond will be stretched from the equilibrium nuclear distance (Re) in the neutral molecule to a critical distance (Rc), and the CE process occurs at this critical distance.[6,23–28] Schmidt et al.[29] explained this phenomenon on the basis of a laser-induced stabilization, and found that the bond elongation is mainly determined by the molecule itself. Based on this viewpoint, Corkum et al.[4] proposed a theoretical model of laser-induced electron localization enhanced ionization, which concluded that the ionization of the parent ion will be dramatically enhanced around the critical distance Rc since the electron can directly tunnel through the narrow internal barrier to the continuum. Similarly, Bandrauk et al.[5,6] presented a charge resonance enhanced ionization model, and showed that the enhanced ionization probability at the critical distance Rc is attributed to the transitions between a pair of charge-resonant states that are strongly coupled to the laser field.
As a prototypical linear triatomic molecule, the photoionization and photodissociation of CO2 and CS2 molecules under the intense femtosecond laser fields have been extensively studied. As a representative study of the CO2 molecule, Wu et al.[30,31] studied the three-body fragmentation dynamics of CO2 molecule in intense laser fields by using a triple ion coincidence technique, and showed that the geometric structure of  before fragmentation is close to that of neutral CO2, and both the sequential and non-sequential fragment processes can occur in the parent ions
before fragmentation is close to that of neutral CO2, and both the sequential and non-sequential fragment processes can occur in the parent ions 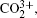 while the parent ions
while the parent ions  can only produce the non-sequential fragment process. In the studies of the CS2 molecule, Graham et al.[32] measured the angular distributions of those fragment ions from the CE process of parent ions, and found that the distribution of fragment ions Sm+ is perpendicular to that of fragment ions Cn+. Mathur et al.[33] defined CS2 molecule as the boundary between a “heavy” molecule (like I2 or its derivatives) and a “light” molecule (like H2 or N2), and showed that the geometric alignment mechanism dominates for the 100-fs laser pulses, while dynamic alignment occurs for the 35-ps laser pulses. Yamanouchi et al.[18–20] utilized a triple coincidence momentum imaging technique to study both sequential and non-sequential three-body CE processes, i.e.,
can only produce the non-sequential fragment process. In the studies of the CS2 molecule, Graham et al.[32] measured the angular distributions of those fragment ions from the CE process of parent ions, and found that the distribution of fragment ions Sm+ is perpendicular to that of fragment ions Cn+. Mathur et al.[33] defined CS2 molecule as the boundary between a “heavy” molecule (like I2 or its derivatives) and a “light” molecule (like H2 or N2), and showed that the geometric alignment mechanism dominates for the 100-fs laser pulses, while dynamic alignment occurs for the 35-ps laser pulses. Yamanouchi et al.[18–20] utilized a triple coincidence momentum imaging technique to study both sequential and non-sequential three-body CE processes, i.e.,  and demonstrated that the significant structural deformation occurs for
and demonstrated that the significant structural deformation occurs for  along both bending and stretching coordinates. In previous studies, this coincidence measurement technique can identify a specific single event of Coulomb explosion from a single parent ion, but it has relatively high requirement for the chamber vacuum pressure and sample vapor temperature. Recently, the DC-sliced ion imaging technique has shown to be a well-established tool to study the molecular photoionization and photodissociation process, where both the speed and angular distributions of the produced ions can be directly measured without any mathematical transformation, and so can provide a more intuitive method. In this paper, we experimentally investigate the CE process of CS2 molecule under an intense near-infrared (800 nm) femtosecond laser field by the DC-sliced ion imaging technique. The DC-sliced images of four ions S+, S2+, CS+, and CS2+ by breaking one C–S bond are measured, and their Coulomb explosion channels are assigned by calculating kinetic energy release (KER) and their angular distributions are extracted from the DC-sliced images. The dissociation dynamics of parent ions
along both bending and stretching coordinates. In previous studies, this coincidence measurement technique can identify a specific single event of Coulomb explosion from a single parent ion, but it has relatively high requirement for the chamber vacuum pressure and sample vapor temperature. Recently, the DC-sliced ion imaging technique has shown to be a well-established tool to study the molecular photoionization and photodissociation process, where both the speed and angular distributions of the produced ions can be directly measured without any mathematical transformation, and so can provide a more intuitive method. In this paper, we experimentally investigate the CE process of CS2 molecule under an intense near-infrared (800 nm) femtosecond laser field by the DC-sliced ion imaging technique. The DC-sliced images of four ions S+, S2+, CS+, and CS2+ by breaking one C–S bond are measured, and their Coulomb explosion channels are assigned by calculating kinetic energy release (KER) and their angular distributions are extracted from the DC-sliced images. The dissociation dynamics of parent ions  is numerically simulated by using a Coulomb energy approximation, and it is shown that the dissociation time decreases when the charge number increases.
is numerically simulated by using a Coulomb energy approximation, and it is shown that the dissociation time decreases when the charge number increases.
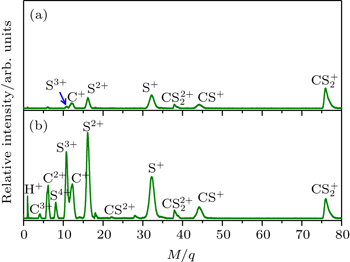
3. Results and discussionFigure 1 shows two typical TOF mass spectra of CS2 molecule irradiated by the 800-nm femtosecond laser field with a laser central wavelength of 800 nm and the pulse duration of 70 fs for the laser intensity of 4.9 × 1013 W/cm2 (see Fig. 1(a)) and 1.3 × 1014 W/cm2 (see Fig. 1(b)). In our experiment, the laser polarization direction is always perpendicular to the TOF axis. When the laser intensity is set at 4.9 × 1013 W/cm2, as shown in Fig. 1(a), these fragment ions C+, Sm+ (m = 1–3), CS+,  and
and 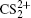 can be observed, which indicates that the two C–S bonds can be broken in this lower laser intensity. When the laser intensity is increased to 1.3 × 1014 W/cm2, as shown in Fig. 1(b), some highly charged fragment ions C2+, C3+ and S4+ appear, which shows that the appearance potential of fragment ion Cm+ is higher than that of fragment ion Sm+ with the same charge number. Generally, the generation of highly charged ions (such as C2+, C3+, S2+, S3+, S4+) indicates the participation of the CE processes in our experiment. In addition to the two parent ions
can be observed, which indicates that the two C–S bonds can be broken in this lower laser intensity. When the laser intensity is increased to 1.3 × 1014 W/cm2, as shown in Fig. 1(b), some highly charged fragment ions C2+, C3+ and S4+ appear, which shows that the appearance potential of fragment ion Cm+ is higher than that of fragment ion Sm+ with the same charge number. Generally, the generation of highly charged ions (such as C2+, C3+, S2+, S3+, S4+) indicates the participation of the CE processes in our experiment. In addition to the two parent ions  and
and  no other multiply charged parent ions are observed at the full range of our laser intensities, which may be due to the instability of the highly charged parent ions. In this work, we aim to explore the formation mechanism of fragment ions S+, S2+, CS+, and CS2+ by breaking one C–S bond.
no other multiply charged parent ions are observed at the full range of our laser intensities, which may be due to the instability of the highly charged parent ions. In this work, we aim to explore the formation mechanism of fragment ions S+, S2+, CS+, and CS2+ by breaking one C–S bond.
When the polyatomic molecules are subjected to an intense femtosecond laser field, the fragment ions can be produced from different photoionization and photodissociation channels. With the help of DC-sliced image technique, we can clearly discriminate these different dissociative ionization channels of the fragment ions with same mass-to-charge ratio. Figure 2 presents the pseudo-color DC-sliced images of fragment ions S+, S2+, CS+, and CS2+. One can see that each fragment ion involves more than one dissociative ionization channel. Usually, the fragment ions with high KER should result from the CE process, while those with low KER should result from the multi-photon dissociative ionization process. Here we focus on the CE process of the four fragment ions. As is well known, in the two-body CE model, the two partner ions should meet with the momentum conservation condition. In other words, the KERs of the two fragments should satisfy the following relationship:[27,35,36]
where
X and
Y represent the partner fragment ions,
M is the mass of corresponding fragment ions, and
p,
q are charge numbers of the two fragment ions. Figure
3 shows the velocity distributions of the four fragment ions S
+, S
2+, CS
+, and CS
2+, and the calculated kinetic energies of these different peaks are also labeled. In order to facilitate the discussion below, these peaks from low to high kinetic energy are respectively labeled with the symbols P
x (
x = 1–3). According to Eq. (
1), it can be deduced that P
1 peak in the fragment ion S
+ and P
2 peak in the fragment ion CS
+ should come from the two-body CE process,
Applying the same method, P
3 peak in the fragment ion S
+ and P
2 peak in the fragment ion CS
2+ can be assigned to the two-body CE process,
while the P
1 peak in the fragment ion S
2+ and P
3 peak in the fragment ion CS
+ can be attributed to such a two-body CE process,

Similarly, the P
2 peak in the fragment ion S
2+ and P
3 peak in the fragment ion CS
2+ can be verified as the two-body CE process below,
However, we cannot find a corresponding peak in Fig.
3 to match P
3 peak in fragment ion S
2+, whose partner ion might experience further dissociation or CE process.
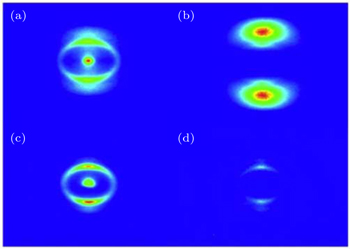
Table 1 lists the mass ratio M(CSq+)/M(Sp+), KER ratio (Sp+)/KER(CSq+), and relative experimental error Δ. Considering the experimental condition and data processing, if the experimental error Δ is less than 5%, the above listed channel assignments are considered to be correct. As can be seen, both the channels (1,2) and (2,1) result from the CE process of parent ion 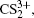 but their total KERs are different, which can come from the different precursor states. In addition, there is a spot in the central position for the fragment ions S+ and CS+, which can be assigned to the (1,0) and (0,1) dissociative ionization channels of parent ion
but their total KERs are different, which can come from the different precursor states. In addition, there is a spot in the central position for the fragment ions S+ and CS+, which can be assigned to the (1,0) and (0,1) dissociative ionization channels of parent ion 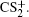 Here, we do not discuss this dissociation process since our focus is the CE process.
Here, we do not discuss this dissociation process since our focus is the CE process.
In addition to the KER distribution, the angular distribution of fragment ions also plays an important role in assigning the dissociation channels. The two fragment ions from the same dissociation channel should have the similar angular distribution. Figure 4 presents the angular distributions of four pairs of fragment ions mentioned above. As expected, each pair of fragment ions has a similar angular distribution, which can further verify the above CE channel assignments. Furthermore, one can see that the fragment ions that result from the dissociation process of the higher parent ions will show a narrower angular distribution.
It has been proved that the total KER Etotal from the CE process and the critical distance Rc should satisfy the following relationship:[23,26]

The calculated
Rc values for the four channels are also shown in Table
1. It can be found that the chemical bond fusion in all these channels takes place at the critical distance
Rc between 3.66 and 4.19 Å, which is about 2.3–2.7 times longer than the equilibrium distance of C–S bond (1.56 Å). It is noted that the bond elongation is larger for the parent ion with a larger charge number, and this phenomenon has been observed in diatomic and triatomic molecules.
[37–41] The bond elongation has been explained by an enhanced ionization at a critical distance
Rc where the ionization rate would be greatly enhanced, and the intense Coulomb repulsive energy will lead to the dramatic fragmentation process by converting the Coulomb energy into the KERs of the two separated fragment ions.
[4–6]To better understand this energy conversion process, we use a Coulomb potential approximation to theoretically simulate the dissociation process of parent ions, and here the doubly charged parent ion 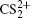 is used as an example for detailed illustration. Assuming that the initial momentum of fragment ions S+ and CS+ are both zero, the critical distance Rc of parent ion
is used as an example for detailed illustration. Assuming that the initial momentum of fragment ions S+ and CS+ are both zero, the critical distance Rc of parent ion  is known as 3.75 Å, and the two fragment ions S+ and CS+ move along the Coulomb potential. Here, we introduce the Hamiltonian in the center-of-mass coordinate system as follows:
is known as 3.75 Å, and the two fragment ions S+ and CS+ move along the Coulomb potential. Here, we introduce the Hamiltonian in the center-of-mass coordinate system as follows:
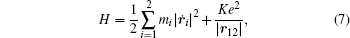
where
K = 1/4
πɛ0, and subscript 1 and 2 represent the two fragment ions S
+ and CS
+, respectively. By simplifying, equation (
7) can be further written as follows:
[28]
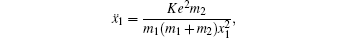

with the initial conditions,
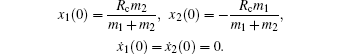
In our simulation, equation (
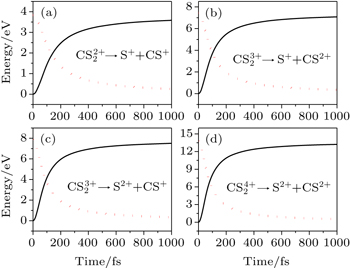
8) is solved numerically, and the time evolution of Coulomb energy and KERs in the above four channels can be obtained, as shown in Fig.
5. Obviously, the Coulomb energy dramatically decreases while KER accordingly increases for all these channels. In order to intuitively understand the energy conversion, the time requirements for different percentages of Coulomb energy to KERs in each channel are listed in Table
2. We assume that the time requirement for the energy conversion percentage of 90% is defined as the dissociation time of the parent ion,
[28] which means that the C–S bond is completely broken and the parent ion

dissociates into two fragment ions S
p+ and CS
q+ within that time, and thus the dissociation time of these parent ions
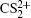
(channel (1, 1)),
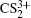
(channel (1, 2)),
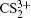
(channel (2, 1)), and
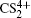
(channel (2, 2)) are about 666, 498, 456, and 396 fs, respectively. It is noteworthy that the time requirement for the dissociation becomes shorter with the increase of the charge number of the parent ion. That is to say, the higher charge number will yield the stronger Coulomb repulsive force, which will accelerate the Coulomb explosion and quickly dissociate into fragmentation ions, and so the higher KER and narrower angular distribution of the fragment ions will be observed. This gives a good explanation for the experimental observation in Figs.
3 and
4 that the fragment ions with the higher KER and narrower angular distribution come from the higher parent ions. Moreover, the change tendency of the dissociation time can help us understand why no highly charged parent ions
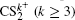
are observed in our experiment, as shown in Fig.
1.
Table 2.
Table 2.
 Table 2. Time requirement for different percentages of Coulomb energy to KERs in the four CE channels. .
| Channels |
10% |
30% |
50% |
70% |
90% |
| (1,1) |
41 |
84 |
136 |
237 |
666 |
| (1,2) |
30 |
62 |
100 |
176 |
498 |
| (2,1) |
27 |
56 |
94 |
162 |
456 |
| (2,2) |
24 |
49 |
91 |
140 |
396 |
| Table 2. Time requirement for different percentages of Coulomb energy to KERs in the four CE channels. . |