Sulfur-containing species have received growing attention due to their important role played in the air pollution and acid rain.^[1–7] Among various sulfur-containing compounds, the HS₂ radical is one of the most important species, which is responsible for the oxidation of reduced forms of sulfur, the reaction in combustion^[8–10] and biochemistry.^[11,12] Therefore, extensive studies on the HS₂ radical have been carried out both theoretically and experimentally for decades.

Among a vast array of theoretical studies, Sannigrahi et al.^[13] performed CI calculations and provided both structural and vibrational information of the electronic ground and excited states of HS₂. Zhou et al.^[14] carried out investigations on the geometries and spectroscopic parameters of the XS₂ (X = H, F, Al, and Br) radicals using the split-valence plus polarization function and larger basis sets at the self-consistent field (SCF) and the second order Møller–Plesset (UMP2). By employing the CCSD(T) theory, the equilibrium structure and vibrational frequencies were reported by Owens et al.^[15] for the X₂H hydrides (X = Al, Si, P, and S) at their global minima. Subsequently, more accurate structural and thermodynamic properties of the HS₂ radical were obtained by Denis^[16] using the CCSD(T) and B3LYP levels of theory. Later, the accurate three-dimensional, near-equilibrium potential energy and dipole moment functions for both the ground and the first electronic excited states of HS₂ were constructed by Peterson et al.^[17] by using highly correlated coupled cluster methods with explicit basis set extrapolation. Song et al.^[18] reported an accurate double many-body expansion (DMBE) potential energy surface (PES) for ground-state HS₂ based on ab initio energies extrapolated to the complete basis set limit. Quite recently, Qin et al.^[7] calculated the equilibrium geometry of the first excited electronic state of HS₂ by time-dependent density functional theory using the hybrid functional B3LYP with the aug-cc-pVQZ (AVQZ) basis set.

The vibrational frequencies of the ground state (X²A″) and the excited state (A²A′) of HS₂ were investigated by Holstein et al.^[19] By studying the microwave spectroscopy of the ground electronic state of HS₂, Yamanoto and Saito^[20] reported the lowest energy structure. Ashworth et al.^[21] first observed the far infrared laser magnetic resonance (LMR) spectrum of the ground state of HS₂. Subsequently, Isoniemi et al.^[22] investigated more refined structural information of HS₂ radical in Ar matrix following the 266 nm photolysis of H₂S₂. The S–H stretching and the S–S–H bending modes were observed at 2463 cm⁻¹ and 903 cm⁻¹, respectively. Ashworth and Fink^[23] analyzed the X–A band system through high-resolution Fourier-transform measurements of the chemiluminescence spectra of both HS₂ and DS₂. Entfellner and Boesl^[24] presented the photodetachment-photoelectron spectra of the ground and the first excited states of HS₂ and DS₂ with a conventional time of flight photoelectron spectrometry.

Indeed, as far as we are aware, there is no work toward obtaining a global PES for the first electronic excited state of HS₂(A²A′) reported, which would be of interest to the investigations of the H(²S) + S₂(a¹Δ_g)→ SH(X²Π) + S(³P) reaction. Thus, the major goal of the present work is to obtain a high quality global PES of HS₂(A²A′) based on the DMBE^[25–28] methodology.

This paper is organized as follows. Section 2 describes the ab initio calculations employed in the present work. Section 3 presents a brief description of the analytical DMBE formalism. Then the major topographical features of the HS₂(A²A′) PES are discussed in Section 4. The concluding remarks are summarized in Section 5.

The ab initio calculations have been carried out at the multi-reference configuration interaction level^[29,30] of theory, including the Davidson correction [MRCI(Q)],^[31] using the full valence complete-active-space self-consistent field (CASSCF)^[32] wave function as the reference. The AVQZ basis set of Dunning^[33,34] is employed, and the ab initio calculations are performed using the Molpro 2012 package.^[35] A grid of 2767 ab initio points is chosen to map the PES over the H–S₂ region defined by 2.5 ≤ R_S2/a₀ ≤ 5.5, 0.2 ≤ r_H−S2/a₀ ≤ 15, 0° ≤ γ/≤ 90°, and for the S–SH interactions, 2.0 ≤ R_SH/a₀ ≤ 4.0, 0.6 ≤ r_S−SH/a₀ ≤ 15, 0° ≤ γ/≤ 180°, where R, r, and γ are the atom–diatom Jacobi coordinates. The C_s point group symmetry is employed in the ab initio calculations, which holds two irreducible representations A′ and A″. For HS₂(A²A′), seven A′ and two A″ symmetry molecular orbitals (MOs) are determined as the active space, amounting to 214 (136A′ + 78A″) configuration state functions. The MOs which correlate with the 3s and 3p atomic orbitals of each S and the 1s orbital of the H atom are utilized to determine the valence space.

The ab initio energies calculated in this way have been subsequently corrected using the double many-body expansion-scaled external correlation method (DMBE-SEC)^[36] to account for the excitations beyond singles and doubles, most importantly, for incompleteness of the basis set. According to the DMBE-SEC scheme, the total DMBE-SEC interaction energy is written as

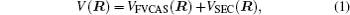
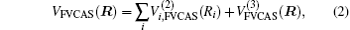
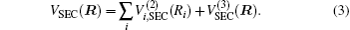
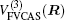
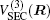
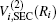
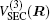
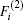
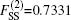
In the framework of DMBE methodology, the single-sheeted PES can be written as

3.1. Two-body energy terms

The diatomic potential energy curves (PECs) of S₂(a ¹Δ_g) and SH(X²Π), which show the correct behaviors at the asymptotic limits R→ 0 and R → ∞, have been modeled using the EHF approximate correlation energy method.^[40,41]

The EHF-type energy term is written as

where

Here r = R − R_e is the displacement from the equilibrium diatomic geometry; D, a_i (i = 1,…,7), and γ_i (i = 0,1,2) are adjustable parameters to be obtained from a least-square fitting procedure.

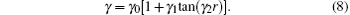
In turn, the dc energy term is written as^[42]

with the damping functions for the dispersion coefficients assuming the form

where A_n = α₀n^−α₁ and B_n = β₀exp(−β₁n) are auxiliary functions. The α₀, β₀, α₁, and β₁ are universal dimensionless parameters for all isotropic interactions: α₀ = 16.36606, α₁ = 0.70172, β₀ = 17.19388, and β₁ = 0.09574. Moreover, ρ/a₀ = 5.5 + 1.25R₀, where is the LeRoy parameter,^[43] and and are the expectation values of the squared radii for the outermost electrons in atoms A and B, respectively.

3.2. Three-body energy terms

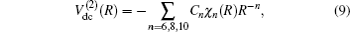
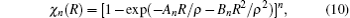
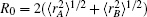
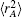
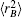
As usual,^[44,45] the three-body dc energy term is written in the following functional form:

where R_i is the corresponding diatomic internuclear separation, r_i is the distance between atom A and the center-of-mass of diatom BC, and θ_i is the angle between these two vectors. f_i(R) = {1 − tanh[ξ (ηR_i − R_j − R_k)]}/2 is a switching function. As was done in Ref. [37], we have used η = 6 and ξ = 1.0a₀⁻¹. The χ_n(r_i) in Eq. (11) is a damping function, which is written in the functional form employed elsewhere.^[37,44] As was done for NH₂(2²A″),^[46] the parameters of are taken from Ref. [18] for the ground electronic state of HS₂.

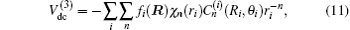
For a given triatomic geometry, by removing the sum of the two-body energy terms from the corresponding interaction energies, one obtains the total three-body energy. Then by subtracting the three-body dc contribution from the total three-body energy, the three-body EHF energy contribution is obtained. It can be modeled in the three-body distributed-polynomial^[47] form

where P^j(Q₁,Q₂,Q₃) is the j-th polynomial up to six-order in symmetry coordinates, which is defined as

In the above equation, , , and , with Q_i (i = 1,2,3) being the symmetry coordinates defined as

In turn, are the reference geometries and are the nonlinear range-determining parameters, which are optimized via a trial-and-error least-squares fitting procedure^[48,49] that minimizes the root-mean-squared deviation (rmsd) error while warranting the proper behavior in the asymptotic region. The complete set of parameters totals 150 linear coefficients, 9 nonlinear ones, and 9 reference geometries. Table 1 shows the rmsd values of the final DMBE/SEC PES with respect to all the fitted ab initio energies. As shown in Table 1, a total of 2676 points have been used for the calibration procedure, thus covering a range up to 400 kcl·mol⁻¹ above the HS₂ global minimum.

Table 1.

Table 1.

Table 1. Root-mean-square deviations (in kcal·mol−1) of the PES. . Energy/kcal·mol−1 Na rmsd 10 24 0.206 12 20 65 0.491 14 30 133 0.925 34 40 217 1.046 54 50 321 1.103 91 60 769 1.221 148 70 1157 1.279 193 80 1286 1.321 224 90 1703 1.276 307 100 1807 1.289 333 200 2520 1.341 443 300 2631 1.371 463 400 2676 1.406 46 a Number of points in the indicated energy range. b Number of points with an energy deviation larger than the rmsd.

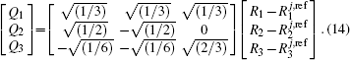
Table 1. Root-mean-square deviations (in kcal·mol−1) of the PES. .

The fitted potential energy curves of S₂(a ¹Δ_g) and SH(X²Π) and the deviations from the MRCI(Q)/AVQZ energies are displayed in Fig. 1. As shown in Fig. 1, the modeled PECs show smooth behaviors and accurately mimic the ab initio energies, with the maximum error being smaller than 0.05 kcal · mol⁻¹. Parameters gathered in Table 2 include the equilibrium geometry (R_e), dissociation energy (D_e), harmonic vibrational frequency (ω_e), non-harmonic vibrational frequency (ω_ex_e), and rotational constants (α_e and β_e). Excellent agreement can be found in Table 2 between the results obtained from the modeled PECs and the experimental data. For SH(X²Π), the deviations for R_e, D_e, ω_e, ω_ex_e, α_e, and β_e are calculated to be 0.0002 a₀, 0.3948kcal · mol⁻¹, 5.736 cm⁻¹, 0.447 cm⁻¹, 0.0346 cm⁻¹, and 0.1304 cm⁻¹, respectively, while the corresponding deviations for S₂(a ¹Δ_g) are 0.0199 a₀, 0.15 cm⁻¹, 0.845 cm⁻¹, 0.00017 cm⁻¹, and 0.0033 cm⁻¹. Good agreement is also found compared to other theoretical results.^{[17,18,50–53]}

Fig. 1.

	Figure Option ViewDownloadNew Window
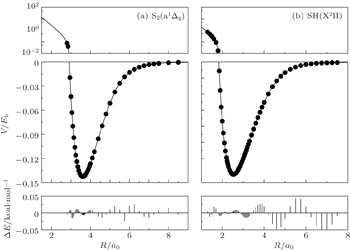	Fig. 1. Potential energy curves of (a) S2(a 1Δg) and (b) SH(X2Π), and the differences between the fitted PECs and the ab initio points.

Table 2.

Table 2.

Table 2. Spectroscopic constants of SH and S2 diatoms, Re is in the units of a.u., De is in the units of kcal · mol−1, and ωe, ωexe, αe, and βe are in the units of cm−1. . Re De ωe ωexe αe βe SH(X2Π) This work 2.5337 87.7448 2701.536 59.453 0.3046 9.5965 Theor.[18] 2.5354a 87.77a 2697.5a – – – Theor.[17] 2.5325b 87.56b 2701.2b – – – Theor.[58],c 2.5376 87.13 2699.8 47.706 0.2639 9.4414 Exp.[59,60] 2.5339 87.35±0.7 2695.8 59.9 0.270 9.4611 S2(a 1Δg) This work 3.6079 89.5674 702.20 3.935 0.0019 0.2893 Theor.[50] 3.6007 89.5322 700.81 3.921 0.0019 0.2905 Theor.[51] 3.5972 89.0832 699.68 3.102 0.0017 0.2911 Theor.[52] 3.6050 – 746 – 0.0014 0.2897 Theor.[53] 3.6070 – 697.0 – – – Exp.[59] 3.588 – 702.35 3.09 0.00173 0.2926 a Obtained from HS2(X 2A″) PES. b The dissociation energies are calculated by De = D0 + ωe/2. c Obtained at CCSD(T)/AV5Z level of theory.

Table 2. Spectroscopic constants of SH and S2 diatoms, Re is in the units of a.u., De is in the units of kcal · mol−1, and ωe, ωexe, αe, and βe are in the units of cm−1. .

Figures 2–4 illustrate the major topographical features of the HS₂(A²A′) DMBE/SEC PES, and the corresponding structural parameters of the stationary points are collected in Table 3, including our ab initio values calculated at the MRCI(Q)/AVQZ level of theory and other theoretical and experimental results. The global minimum obtained from the present DMBE/SEC PES locates at R₁ = 3.937a₀, R₂ = 2.540a₀, and R₃ = 4.836_a0 (R₁ is the SS interatomic separation, while R₂ and R₃ are the two SH interatomic separations), differing only 0.025a₀, 0.002a₀, and 0.003a₀ from the MRCI(Q)/AVQZ results, respectively. Compared with the theoretical works of Peterson et al.^[17] and Denis,^[16] the maximal differences occur in R₃, which are only 0.043 a₀ and 0.025 a₀, respectively. Since the DMBE-SEC method is employed to model the ab initio energies, the well depth of the global minimum is 0.0078E_h lower than that of MRCI(Q)/AVQZ. As for the harmonic frequencies, the DMBE/SEC PES from the present work predicts values of 2714.19 cm⁻¹, 504.45 cm⁻¹, and 812.27 cm⁻¹, which are in good agreement with the most recent experimental values given by Qin et al.,^[7] which are 2585 ± 81 cm⁻¹, 490 ± 41 cm⁻¹, and 741 ± 41 cm⁻¹, respectively. Table 3 also gathers the properties of three saddle points (SP): SP1 (D_∞v), SP2 (C_∞v), and SP3 (C_∞v), and two transition states (TS): TS1 (C_2v) and TS2 (C_∞v).

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Contour plots of HS2 (A2A′) potential energies for the four H–S–S angles (a) 0°, (b) 45°, (c) 90°, and (d) 135°. Contours are equally spaced by 0.006Eh, starting from −0.1668Eh in panel (a), −0.1977Eh inpanel (b), −0.2294Eh in panel (c), and −0.2006Eh in panel (d).

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Minimum energy paths for HS2(A2A′) PES at four H–S–S angles.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. The spherically averaged isotropic (V0) and leading anisotropic potentials (V2): (a) for H + S2 interaction, with RSS = 3.6079a0; (b) for S + SH interaction, with RSH = 2.5337a0.

Table 3.

Table 3.

Table 3. Properties of stationary points on the fitted HS2(A2A′) PES (harmonic frequencies in cm−1). . Feature R1/a0 R2/a0 R3/a0 E/Eh ωH − S ωS − S ωbending Global minimum DMBE/SEC PES 3.937 2.540 4.836 −0.2298 2714.19 504.45 812.71 MRCI(Q)/AVQZ 3.962 2.538 4.833 −0.2220 2640.73 425.84 862.64 Theor.[17] 3.923 2.536 4.790 – 2674.1 513.0 770.5 Theor.[16] 3.942 2.538 4.808 – 2683 501 765 Theor.[15] – – – – 2706 517 794 Exp.[23] – – – – 504.5 808 ± 10 Exp.[24] – – – – 2550 ± 200 750 ± 200 Exp.[7] – – – – 2585 ± 81 490 ± 41 741 ± 41 TS1 (C2v) DMBE/SEC PES 3.987 2.965 2.965 −0.1889 1406.44 481.93 1823.40i MRCI(Q)/AVQZ 3.933 2.928 2.928 −0.2006 1932.39 541.41 1395.79i TS2 (C∞v) DMBE/SEC PES 3.891 6.445 2.555 −0.1667 2446.84 478.52 712.60i MRCI(Q)/AVQZ 3.991 6.829 2.838 −0.1476 1154.95 309.25 407.15i SP1 (D∞v) DMBE/SEC PES 5.870 2.935 2.935 −0.1241 1756.21i 385.43 225.78i MRCI(Q)/AVQZ 6.042 3.021 3.021 −0.1153 2668.31i 295.29 273.13i SP2 (C∞v) DMBE/SEC PES 3.652 4.265 7.917 −0.1288 219.85i 724.26i 628.07 SP3 (C∞v) DMBE/SEC PES 5.457 2.537 7.994 −0.1392 474.65i 193.09i 2656.44

Table 3. Properties of stationary points on the fitted HS2(A2A′) PES (harmonic frequencies in cm−1). .

The contour maps for the H(²S) + S₂(a¹Δ_g) → SH(X ²Π) + S(³P) reaction in internal coordinates at four H–S–S angles (∠HSS = 0°, 45°, 90°, and 135°) are shown in Fig. 2. The contours are equally spaced by 0.006E_h, starting at −0.16681E_h for 0°, −0.19773E_h for 45°, −0.22936E_h for 90°, and −0.20061E_h for 135°. The notable feature observed is that there are two valleys in each map: the left upper valley corresponds to H(²S) + S₂(a¹Δ_g) asymptote, while the valley at the right bottom corresponds to SH(X²Π) + S(³P) asymptote. It can also be seen in Fig. 2 that deep wells connect the two asymptotes. For a better understanding of the characteristics of the present PES, the minimum energy paths (MEPs) of the H(²S) + S₂(a¹Δ_g) → SH(X ²Π) + S(³P) reaction at the four H–S–S angles are shown in Fig. 3. These MEPs represent the potential energies of HS₂(A²A′) as a function of a suitable reaction coordinate defined as R_S2 − R_SH, where R_S2 and R_SH are the S–S and S–H internuclear distances, respectively. The R_S2 approaches the S₂ equilibrium distance when the reaction coordinate is large, whereas a large positive reaction coordinate corresponds to R_SH approaching the SH equilibrium distance. The exothermicity of the H(²S) + S₂(a¹Δ_g)→SH(X²Π) + S(³P) reaction is 3.6 kcal · mol⁻¹. The salient feature when ∠HSS = 0°, 45°, 90°, and 135° is that there exist the deep wells at 17.30 kcal · mol⁻¹, 36.85 kcal · mol⁻¹, 56.45 kcal · mol⁻¹, and 38.56 kcal · mol⁻¹ relative to the H + S₂ reactant, respectively. As shown in Fig. 3, there also exist barriers when ∠HSS = 0°, 45°, 90°, and the highest barrier (6.459 kcal · mol⁻¹ relative to H + S₂ reactant) is obtained when ∠HSS = 0°, locating at R_S2 = 3.652a₀ and R_SH = 4.265a₀.

Figure 4 shows the spherically averaged isotropic (V₀) and leading anisotropic potentials (V₂) for H + S₂ and S + SH scattering processes. The V_L (L = 0,2) potentials are obtained by expressing the interaction energies in a Legendre expansion^[54–56]

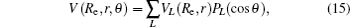
A global accurate PES is reported for HS₂(A²A′) by fitting the MRCI(Q)/AVQZ energies which are scaled by the DMBE-SEC method. The resulting PES is realistic over the entire configuration space. The various topographical features of the current DMBE/SEC PES have been examined in detail and compared with the previous theoretical and experimental results. The properties, including geometries, energies, and vibrational frequencies, have been characterized on the current HS₂(A²A′) DMEB-SEC PES. The results show good agreement with the previous high quality theoretical studies and the available experiment data. Thus, the PES constructed here can be used for dynamic studies of reactions and also as a building block for the PESs of larger molecular systems containing the HS₂ fragment.