† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 61403143), the Natural Science Foundation of Guangdong Province, China (Grant No. 2014A030313739), the Science and Technology Foundation Program of Guangzhou City, China (Grant No. 201510010124), and the Excellent Doctorial Dissertation Foundation of Guangdong Province, China (Grant No. XM080054).
This paper aims at developing a novel method of constructing a class of multi-wing chaotic and hyperchaotic system by introducing a unified step function. In order to overcome the essential difficulties in iteratively adjusting multiple parameters of conventional multi-parameter control, this paper introduces a unified step function controlled by a single parameter for constructing various multi-wing chaotic and hyperchaotic systems. In particular, to the best of the authors’ knowledge, this is also the first time to find a non-equilibrium multi-wing hyperchaotic system by means of the unified step function control. According to the heteroclinic loop Shilnikov theorem, some properties for multi-wing attractors and its chaos mechanism are further discussed and analyzed. A circuit for multi-wing systems is designed and implemented for demonstration, which verifies the effectiveness of the proposed approach.
Chaos control refers to purposefully eliminating or weakening chaotic behavior of a system through some control methods when the chaotic motion is harmful. Since the Ott–Grebogi–Yorke (OGY) method was proposed in 1990,[1] much effort has been devoted to the study of controlling chaos. However, not all chaotic behaviors are harmful, and recent research has shown that chaos can actually be useful under certain circumstances, such as chaos-based multimedia encryption and decryption.[2,3] Therefore, chaotification by making an originally non-chaotic dynamical system chaotic, enhancing existing chaos, or extending the number of saddle focus equilibria for generating multi-wing or multi-scroll chaotic and hyperchaotic systems has attracted some special attention in recent years.[4–13]
Compared with the double wing chaotic system, the multi-wing chaotic system is a new type of generalized Lorenz system characterized by multiple wings which are distributed in a single direction or in multiple directions, the phase portrait for multi-wing chaotic attractor is formed with nested wing, the number and the grid distribution of the wing can be adjusted by parameters.[10] In contrast to the double-wing chaotic system, the multi-wing chaotic system possesses the following features that have potential applications in secure communication: i) the phase trajectories of multi-wing chaotic attractors can randomly jump in all wings with ergodic property, so that the dynamical behavior is more complicated than those of Lorenz system and Chen system, and the statistical properties can be improved; ii) by introducing a nonlinear-function controller, several key parameters of multi-wing chaotic attractors can be easily adjusted, including the width of each segment, amplitude, slope, equilibrium, and turning points. As a result, one can easily control the system equilibrium, the number of scrolls, the shapes and sizes of the scrolls, the spatial distribution of the scrolls, and even the phase trajectories.
It is noticed that, up to now, multiple parameter nonlinear function switching controllers, such as duality-symmetric multi-segment linear function and multi-segment quadratic function, have usually been considered for generating multi-wing chaotic attractors from autonomous three-dimensional (3D) quadratic double-wing chaotic systems as shown in Fig.
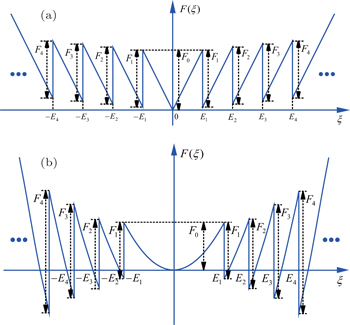 | Fig. 1. Multiple parameter nonlinear functions: (a) multi-segment linear function and (b) multi-segment square function. |
To cope with the above-mentioned issues, this paper introduces a new step function control method with a single parameter ε, which is characterized by the following two aspects.
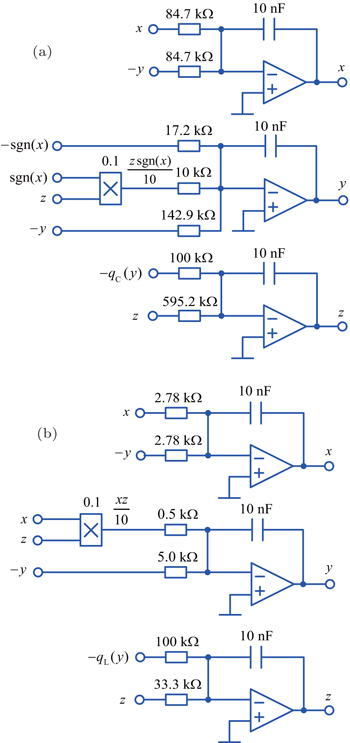
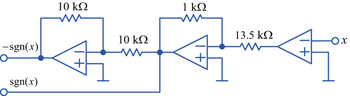
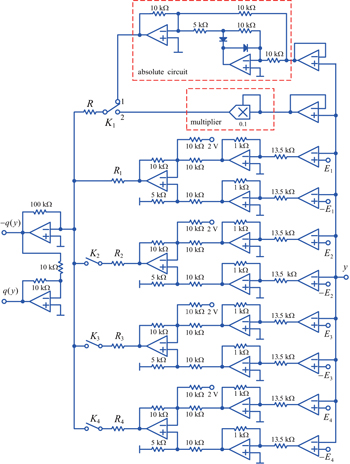
Based on this single parameter ε step function control method, this paper constructs an absolute value piecewise linear 3D multi-wing chaotic system, a square 3D multi-wing chaotic system and a square four-dimensional (4D) multi-wing hyperchaotic system, respectively. According to the heteroclinic loop Shilnikov theorem,[14] the chaos mechanism of absolute value piecewise linear 3D multi-wing chaotic system is analyzed, a circuit for both absolute value piecewise linear and square 3D multi-wing chaotic systems is designed and implemented.
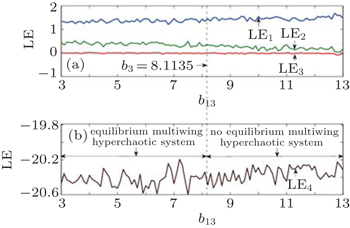
Most reported chaotic systems, i.e., Lorenz system, Chen system, etc, have a limited number of equilibria.[15–18] Therefore, chaos in these systems can be proved by using conventional Shilnikov theorem, in which at least one unstable equilibrium point for emergence of chaos is required. However, it is impossible to use the conventional Shilnikov theorem to verify the chaos in non-equilibrium systems. According to Shilnikov theorem, one or more saddle focus equilibria are keys to the formations of heteroclinic orbit and heteroclinic loop in a chaotic system.[14] For example, double-wing chaotic attractors are formed from saddle or saddle focus equilibria in generalized Lorenz system family,[15–18] and multi-wing chaotic attractors can be constructed by extending the number of saddle focus equilibria.[10–12] As is well known, heteroclinic orbit and heteroclinic loop cannot be formed if there is no equilibrium point. It is noticed that a 4D multi-wing chaotic system was recently found to have no equilibrium point.[19] However, to the best of the authors’ knowledge, there has been no report about a 4D multi-wing hyperchaotic system without equilibrium point so far. One may ask whether there is a possible way further to find a non-equilibrium 4D multi-wing hyperchaotic system. This paper gives a positive answer to the question.
In spite of the fact that a simple non-equilibrium chaotic system was found in 1994,[20] studies on chaotic systems without equilibrium have only bloomed recently.[21,22] It is worth noting that such a chaotic system without equilibrium is categorized as a chaotic system with hidden attraction because its basin of attraction does not intersect with small neighborhoods of any equilibrium.[23] Owing to their academic significance and practical importance, studying systems with hidden attractors has received significant attention.[24]
The rest of the paper is organized as follows. Construction of multi-wing chaotic and hyperchaotic systems via a unified single parameter ε step function control is introduced in Section 2. Some properties of a multi-wing system are discussed and analyzed in Section 3. Circuit design and implementation are demonstrated in Section 4. Finally, in Section 5 some conclusions are drawn.
In this section, two types of double-wing chaotic systems and one type of double-wing hyperchaotic system are first considered. Then, the corresponding multi-wing chaotic system and hyperchaotic system based on a unified single parameter ε step function control are introduced, and the construction criterion for the unified step function is also given.
According to the generalized Lorenz system family,[13–16] two types of double-wing chaotic systems and one type of double-wing hyperchaotic system are given at first. From these systems, one can further obtain the corresponding multi-wing chaotic and hyperchaotic systems by a unified step function switching control.
The n (n = 3,4)-dimensional double wing chaotic or hyperchaotic system is in the form of
According to Eq. (

It is noticed that the third equation in Eq. (
According to Eq. (

It is noticed that the third equation in Eq. (
According to Eq. (
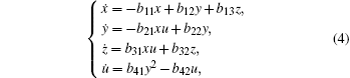
It is noticed that the fourth equation in Eq. (
Based on Eqs. (
According to Eqs. (
Based on Eq. (
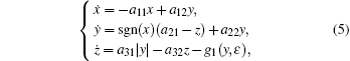
Based on Eq. (
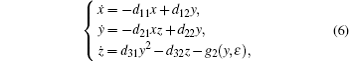
Based on Eq. (
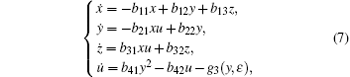
Among Eqs. (
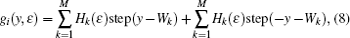
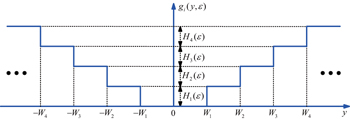
Given Wk (k = 1,2, …,M), the construction criterion for unified single parameter ε even-symmetric step function is described by the following two aspects.
As for g1(y, ε) in Eq. (
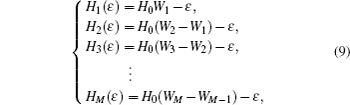
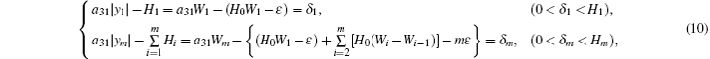
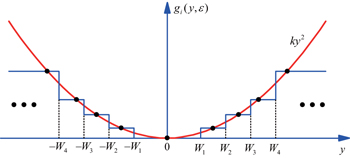
As for g2(y, ε) and g3 (y, ε)in Eqs. (
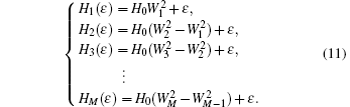
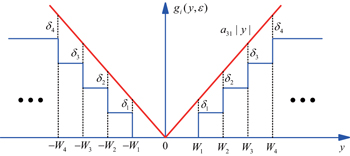 | Fig. 4. Schematic diagram of disjunction between absolute value function a31|y| and step function g1(y, ε). |
For g2 (y, ε), let H0 = d31, W1 = 0.3, W2 = 0.45, …, Wm − Wm−1 = 0.15 (m = 2,3, …,M), and ε = 1.3. For g3 (y, ε), let H0 = b41, W1 = 1.0, W2 = 1.5, …, Wm − Wm−1 = 0.5 (m = 2,3, …,M), and ε = 1.3. When Hk(ε) are determined, to ensure that there is an intersection between square function ky2(k ∈ {d31,b41}) and step function gi (y, ε)(i = 1,2) in each interval (Wi−1, Wi) as shown in Fig.
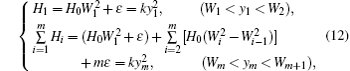
Let M = 4, according to Eqs. (
In this section, the dynamical properties of multi-wing chaotic and hyperchaotic systems generated by the unified step function control are analyzed, including the equilibria of three types of multi-wing systems, non-equilibrium square 4D multi-wing hyperchaotic system, the mechanism analysis for piecewise linear 3D double wing and multi-wing chaotic system, mirror symmetry of multi-wing chaotic system, and the solution of absolute value piecewise linear 3D multi-wing chaotic system.
According to Eq. (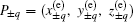
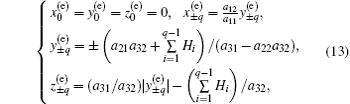

According to Eq. (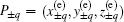
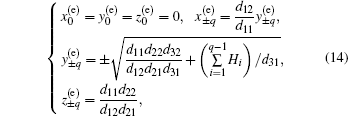
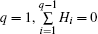
According to Eq. (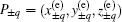
According to Eq. (
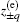
Similarly, according to Eq. (
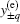
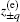
In Eq. (

However, in Eq. (
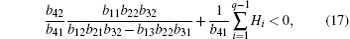
From inequality (
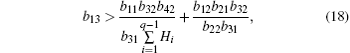
Substituting the above-mentioned parameters into inequality (
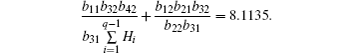
As is well known, the equilibrium point is very important for a chaotic system. Based on the Shilnikov theorem, the key to forming heteroclinic orbit or heteroclinic loop is the existence of one or more saddle focus equilibria in the chaotic system. For example, in a generalized Lorenz system family, double-wing chaotic attractors can be formed from the saddle points or saddle focus points, and multi-wing chaotic attractors can be further formed from extending the number of saddle-focus equilibria. However, without equilibria, the homoclinic orbit or heteroclinic loop cannot be formed. The mechanism for such a kind of non-equilibrium hyperchaotic system needs to be further investigated in depth.
In this section, according to the heteroclinic Shilnikov theorem, the chaotic mechanism analyses for absolute piecewise linear 3D double wing and multi-wing systems are given.
From Eqs. (
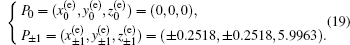
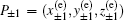
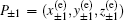
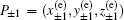
According to heteroclinic Shilnikov theorem, 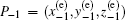
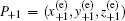
The 1D stable manifold ES(P+1) and the 2D unstable manifold EU(P+1) of 
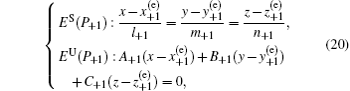
Similarly, the 1D stable manifold ES(P−1) and the 2D unstable manifold EU(P−1) of 
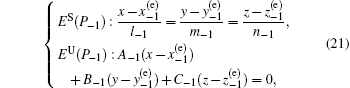
According to Eqs. (
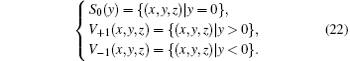
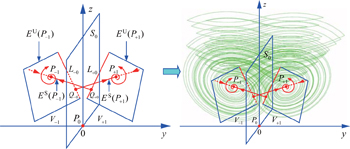 | Fig. 9. Heteroclinic loop connecting two equilibria in absolute piecewise linear 3D double-wing chaotic system. |
If Q+0 lies on L+0, there is a heteroclinic orbit HL1 = EU(P+1) ∪ Q+0 ∪ ES(P−1) from P+1 to P−1. Similarly, if Q−0 lies on L−0, there is a heteroclinic orbit HL2 = EU(P−1) ∪ Q−0 ∪ ES(P+1) from P−1 to P+1. By choosing ai j in Eq. (
Equipped with the controller g1 (y, ε), system (
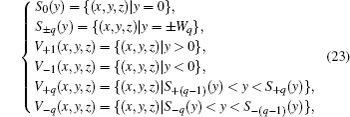
According to Eqs. (

In system (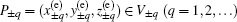
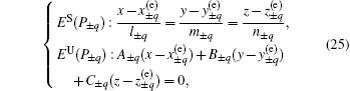
Based on Eq. (
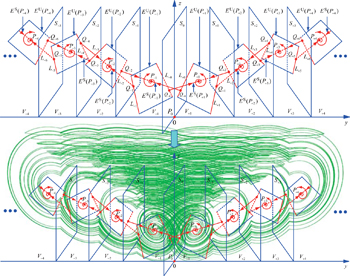 | Fig. 10. Multiple heteroclinic loops connecting multiple adjacent equilibria in absolute piecewise linear 3D multi-wing chaotic system. |
By choosing ai j in Eq. (
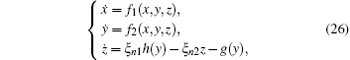
If the corresponding conversion of Eq. (

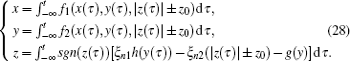
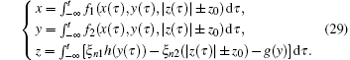

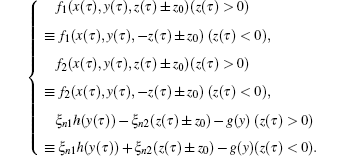
According to Eqs. (
For example, by using the mirror symmetry conversion, system (
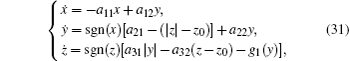
In absolute value piecewise linear 3D double-wing chaotic equation (
It is noticed that the absolute value piecewise linear 3D multi-wing chaotic equation (

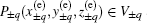
Based on Eqs. (
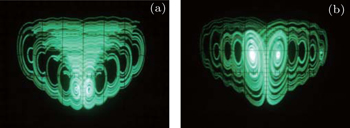
| Table 1. Resistance values and the types of chaotic system in Fig. |
| Table 2. Comparative voltages and the types of chaotic system in Fig. |
| Table 3. On-off for switch linkages K2–K4 and numbers of wings in Fig. |
In this paper, we introduce a novel method of constructing multi-wing butterfly chaotic and hyperchaotic systems via a unified single parameter ε even-symmetric step function control, to overcome the essential difficulties in iteratively adjusting multiple parameters for a conventional multi-parameter control method. By using the proposed strategy, we further find a non-equilibrium 4D multi-wing hyperchaotic system, which is valuable for future investigation due to the significance in basic research and importance in practical application. In addition, some properties for the multi-wing attractor and its chaos mechanism are also discussed and analyzed. The circuits for absolute piecewise linear 3D multi-wing system and for square 3D multi-wing system are designed and implemented for demonstration, respectively.