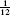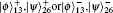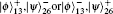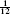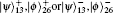† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 61571105), the Prospective Future Network Project of Jiangsu Province, China (Grant No. BY2013095-1-18), and the Independent Project of State Key Laboratory of Millimeter Waves, China (Grant No. Z201504).
Multi-hop teleportation has significant value due to long-distance delivery of quantum information. Many studies about multi-hop teleportation are based on Bell pairs, partially entangled pairs or W state. The possibility of multi-hop teleportation constituted by partially entangled pairs relates to the number of nodes. The possibility of multi-hop teleportation constituted by double W states is 

Quantum teleportation plays a significant role in the quantum communication and has drawn more and more attention in recent decades due to its potential applications.[1–6] Quantum teleportation, first proposed by Bennett et al. in 1993,[7] could transmit quantum information from a source particle to a destination particle by quantum entanglement. Shared entanglement can be achieved by generating an EPR pair and distributing this pair to the source and destination in advance.[8] The first experiment was realized in 1997, and a quantum teleportation distance of 143 kilometers has been achieved by Ma et al.[9]
Long-distance delivery of quantum information is an essential challenge in the future quantum network. Considering the quantum entanglement state can be generated and distributed between smaller segments, quantum repeaters are used as a router to share and distribute quantum entanglement.[10] In recent decades, lots of innovative approaches have been proposed in the quantum teleportation domain.[11–15] In recent years, some significant research works have been done in the domain of multi-hop quantum teleportation. Wang et al.[16] analyzed the multi-hop teleportation based on arbitrary Bell pairs using EPR-pair bridging. The possibility of multi-hop teleportation based on partially entangled state 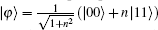

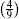
In this paper, we proposed a multi-hop quantum transmission scheme using the combination of W state and EPR pairs and proved its feasibility. The quantum information is transmitted hop by hop via intermediate nodes through the quantum channel established by W state and EPR pairs. We assume that the sender intends to teleport an unknown two-level quantum state: |ψ⟩ = α |00⟩ + β |11⟩ to the receiver. Firstly, we deduce the possibility of successful transmission after one hop teleportation. The recovered qubits are used as the teleported states for the next-hop teleportation. Based on the results of one-hop and two-hop teleportation, we make an assumption about multi-hop possibility and use mathematical induction to prove this assumption. Finally, we obtain a higher possibility of 
The rest of the paper is organized as follows. In Sections 2 and 3, the details of the multi-hop teleportation are discussed and proved, including one-hop, two-hop, and multi-hop teleportation. The conclusions are presented in Section 4. Operations of the Pauli operator used in this paper are introduced in Appendix A.
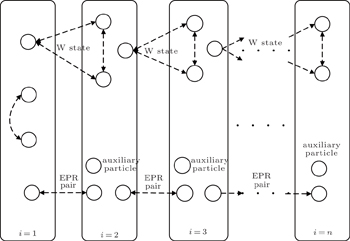
The fidelity of the quantum entanglement decreases as the distance increases in the long-distance quantum transmission. It is practical to transmit quantum states from source to destination in a multi-hop way with more than one intermediate state. In the following two sections, a multi-hop transmission method based on W state and EPR pairs is presented and its validity is verified.
There are two nodes in Fig. 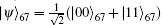
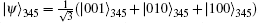
The process of quantum state transmission is described as follows.
According to this process, the entire quantum circuit is given in Fig.
The entire system can be represented as

Considering the following equation:
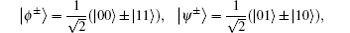
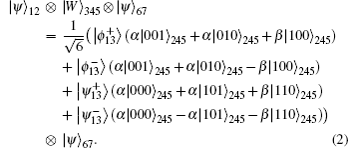
After the Bell measurement on particles 1 and 3, the possibility of getting 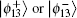
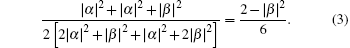
The possibility of getting 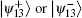
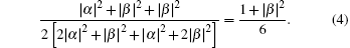
Assuming the measurement result is 
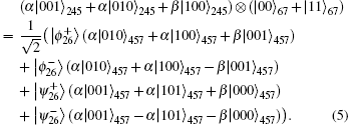
The possibility of getting 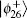

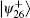
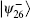
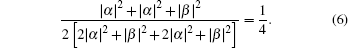
Assuming the measurement result is 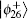
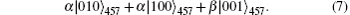
At last, after the measurement, if the |0⟩4 is obtained with the possibility of 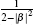
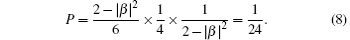
Every destination state can be turned into

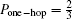
| Table 1. Results of one-hop teleportation for |ψ⟩ 12 ⊗ |W⟩ 345 ⊗ |ψ⟩ 67. . |
As shown in Fig.
From the deduction of one-hop teleportation, after the first teleportation, the four possible states of particles 5 and 7 are: α|10⟩57 ± β|01⟩57, α|01⟩57 ± β|00⟩57, α|00⟩57 ± β|11⟩57, and α|01⟩57 ± β|10⟩57. Assuming that α|00⟩57 + β|11⟩57 (same as α|00⟩57 − β|11⟩57) is achieved at node Bob after one-hop teleportation, the system state can be represented as
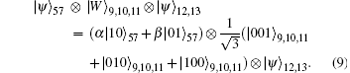
Considering the following equation:

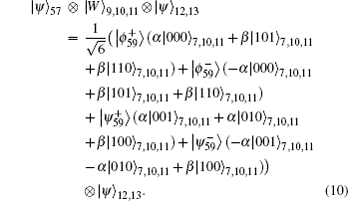
The expression (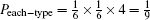
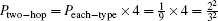
| Table 2. Two-hop teleportation flow charts. . |
According to the results of the 1-hop and 2-hop cases, we consider that the system gets the four-type results: α|10⟩ ± β|01⟩, α|01⟩ ± β|00⟩, α|00⟩ ± β|11⟩, and α|01⟩ ± β|10⟩ after (n−1)-hop teleportation and we assume that the possibility of each type is 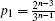

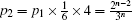
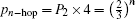
We assume that quantum information at the source node is teleported through a multi-hop quantum channel based on W state and EPR pairs and we deduce the expression of each type of the results at the destination node and its possibility. We also introduce an auxiliary particle and give the corresponding operation of the Pauli operator to recover the message. The possibility of each type is 
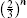
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 |