Random numbers play an important role in many fields, such as statistical analysis, computer simulations, cryptography,^[1] and quantum key distribution (QKD).^[2] Traditionally, there are two different types of random number generators: pseudo random number generators (PRNGs) and true random number generators (TRNGs). Pseudo random number generators require an initial seed as an input, which means that the underlying mathematical algorithm is deterministic. Additionally, as the entropy depends on the length of the random seed, the pseudo random number is not truly random, which limits the actual applications for PRNGs.^[1]

On the other hand, TRNGs use a random sequence which is based on fundamental physical processes, such as a chaotic physical process,^[3,4] a quantum physical process,^[5,6] air turbulence,^[7] radioactive decay,^[8] and random phases.^[9] The indeterministic laws of physics make the output sequences of a random number generator virtually impossible to predict.

In recent years, the probabilistic nature of the quantum physical process is utilized to construct quantum random number generators (QRNGs) whose output is unpredictable. For instance, beam splitter schemes are realized by measuring the path selection of single photons arriving at a 50/50 beam splitter (BS).^[10] The bit rate is another important factor that is exploited to produce high-efficiency QRNGs. Those schemes include vacuum state fluctuations^[11,12] and quantum phase fluctuations,^[13,14] and so far, the fastest TRNGs scheme has already reached 68 Gbps,^[14] which is based on quantum phase fluctuations.

Another natural method to achieve QRNGs is based on the random distribution of the time interval between photons emitted from a single-photon-like source.^[6,15–17] Many current designs based on the arrival time have demonstrated outstanding results.^[18–21] Our group has invested significant effort to overcome some of the limitations of our previous approach.^[17] However, there are still some drawbacks, such as instability, insufficient coding efficiency, a low random bit rate, and a faulty experimental setup.

Furthermore, most of the QRNG schemes that already exist are based on only one random number source.^[9] In those schemes, the properties of the random number source establish the quality of the random number generation. However, it is quite difficult to obtain a satisfactory random number sequence. Additionally, in order to achieve a high-efficiency QRNG, post-processing becomes increasingly complex.^[22] Therefore, it is difficult to make significant improvements to QRNGs with a single random number source. However, another method that can be used is to merge several independent random number sequences, which may already exist as low-efficiency sequences. This makes a high-efficiency QRNG available without requiring complicated processing.

In this paper, we present a hybrid QRNG scheme which combines multiple random number sources. These sources are based on the time of arrival of single photons. Compared with previous studies based on arrival time, the proof-of-concept experiments show that our scheme is simple with a well-performing random nature. It is also practical and fast.

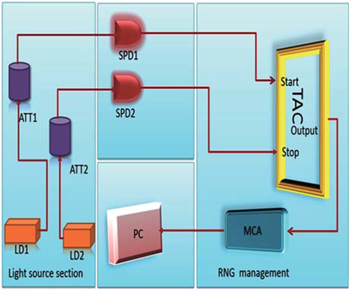
The schematic setup is shown in Fig. 1. For the initial random number source, the arrival times of the dark count or the photons, or both, are suitable for our scheme. The light source section is formed from two independent light sources. Each source consists of a laser diode, an attenuator, and a beam splitter. A pulsed laser diode with a wavelength of 1550 nm, a bandwidth of 3 nm, and a repetition rate of 1 MHz, was used to generate photons. The signals from the laser diode are attenuated so that the average number of photons per pulse is of the order of 0.1. The photons are then connected to two single-photon detectors (SPDs). Note that when the dark count is chosen as the source of the randomness, a light source is not required. The SPD (IDQ, id210-SMF1) performs detection using a fiber-pigtailed InGaAs/InP APD detector which works in Geiger mode with random frequencies ranging from 0 Hz to 1 MHz. The output signals from the SPD are input into a time-to-amplitude converter (TAC) (ORTEC, mod 567). In our scheme, the outputs of SPD1 serve as the start signals and the outputs of SPD2 as the stop signals. This simple configuration merges the two random number sources together, accomplishing the most important aspect of our scheme. Finally, the TAC signals are input into the multichannel analyzer (MCA) (ORTEC, TRUMP-PCI-8K) consisting of m channel addresses. The presence of the variable m enables the channels to be decomposed to almost arbitrary parts by secondary software programming, with every part representing a finite voltage (time) range. In other words, the value of m represents the size of the time interval. Thus, after many repetitions, the probability distribution corresponding to the time of photon arrival can be obtained. At the same time, raw bits can be read into a personal computer (PC) via software connected to the MCA.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Experimental setup of our scheme. LD: laser diode; ATT: attenuator; SPD: single-photon detector; TAC: time-to-amplitude converter; MCA: multichannel analyzer; PC: personal computer.

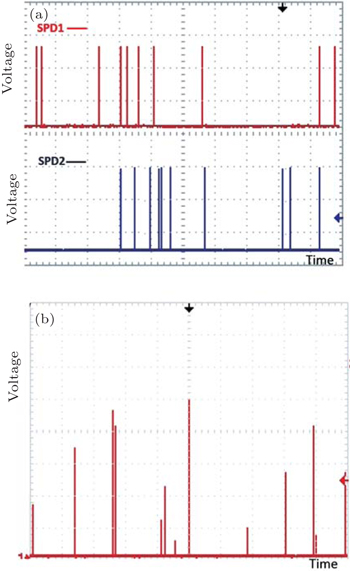
In the first experimental demonstration, the distribution of the time interval of the photons is observed. Figure 2(a) presents the original oscilloscope trace of each random photon of each individual SPD, when the pulsed laser is strongly attenuated to behave like a single-photon source. Intuitively, the time interval between two adjacent signals for every SPD is entirely random. Additionally, the time interval of contiguous photons from two different SPDs is also random. Multiple random sources are combined over the same time period in Fig. 2(b), which shows the original oscilloscope trace of the TAC output, demonstrating the conversion of the time intervals between two different SPDs into voltage pulses. The variation in height of the pulses represents the discrepancy between time intervals, which is completely random.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. (a) Original oscilloscope trace of the photons from each individual SPD. The red line represents the output of the first SPD, while the blue line represents the second one. (b) Original oscilloscope trace of the random photon interval time from the TAC when multiple random number sources are combined together. The height differences correspond to the discrepancies in time intervals.

The data stream from the TAC flowing into the MCA is schematically shown in Fig. 3. When the signal reaches the MCA, the MCA determines the appropriate channel for each count, and adds to the sum of counts at that channel, depending on the voltage value. Furthermore, the PC software acquires the channel information for every single count in real time. Figure 3 demonstrates sampling from the TAC. During actual operation, a frequency of 1 MHz is used for the detector, while the TAC range is set at 200 ns*10. Compared to the theoretical value of 1/8192, it can be clearly observed that the raw data from our scheme follows a uniform distribution very closely. Additionally, the counts in each individual channel also display excellent randomness, which illustrates the randomness of the entire sequence to some extent.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Counts for every channel as seen on the MCA at a frequency of 1 MHz. Number of bins m is 8192 which represents time resolution. The red line represents the average count rate or the ideal uniform distribution, which is equal to 1/m.

Experiments show that the frequencies of SPD and the full-scale time limit (FSTL) of the TAC are the two elements which have the largest effect on the count rate. A diagram for each channel is shown in Fig. 4(a). The three different frequencies are 1 MHz, 100 kHz, or 10 kHz, while the FSTL is 200 ns. Clearly, the distribution for each frequency is almost uniform and higher frequencies have even more uniform distributions. However, the counts at different frequencies have significant discrepancies over the same time span. For the FSTL of the TAC, we select 50 ns*10, 100 ns*10, 200 ns*10 for an SPD frequency of 100 kHz. The corresponding diagram is shown in Fig. 4(b). The distributions of the three different FSTLs are also almost homogeneous. Although the FSTL also has an influence on the counts, this influence is not as dramatic as the frequency. As a result, in order to improve the random bit rate of our QRNG system, higher count rate detectors and more width of FSTL are useful.

Fig. 4.

	Figure Option ViewDownloadNew Window
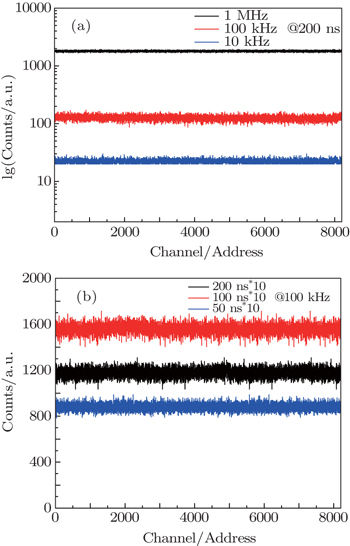	Fig. 4. (a) The counts at different frequencies while the TAC’s FSTL is 200 ns. (b) Number of photons for different FSTL values of the TAC when the SPD frequency is 100 kHz.

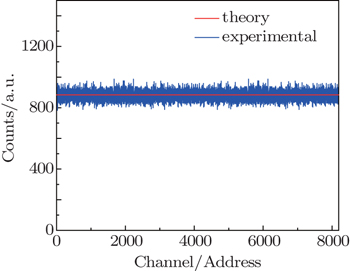
Another way to achieve higher bit rate is to design a high-efficiency coding system. Hence, we carefully coded the data based on the channels where each single output of the TAC was located. As shown in Fig. 5, because the counts and the probability of the time interval distribution for every single channel are almost the same, the coded system can be created according to the channels. For the first step, the number of bits that can be transformed from each individual channel is chosen, denoted by “n”. The scope of n is determined by

This is equivalent to

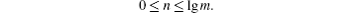
Here m represents the sum over all channels. In our scheme, the variable m is set to 8192, so the variable n must be less than 13. The channels can then be divided into k = m/2³ parts. For each part, the coding scheme is the same as shown in Fig. 5.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. To explain the coding scheme, several points have been extracted from Fig. 3 randomly. Here, taking n = 3 for example, eight (8 = 23) channels are randomly selected from m channels, and can be seen as a group. Channels can be coded in a binary way as shown in the above graph. In this way, m channels can be divided into k = m/2n parts.

For the variable n, practical requirements determine its suitability. In Fig. 5, n = 3 is taken, for example. The MCA allows the status of every channel and every count to be accessed, and allows binary encoding of information in a channel. Finally, by combining the two sets of statistics together, the final random sequence is obtained.

The raw random bits from our QRNG are contributed by both the quantum signal and the classical noise. In order to guarantee that the generated random number is only quantum, the effect of classical noise is also analyzed.

As demonstrated above, the QRNG system which is based on combining multiple random number sources is very stable. Additionally, it can be intuitively observed that the randomness of the raw data is excellent. In order to test the randomness of the raw data, we employed an ENT statistical test suite.^[23] Approximately 10 Gbit of raw data were passed through the ENT tests. One set of results is shown in Table 1.

Table 1.

Table 1.

Table 1. The standard statistical test of ENT. For each scheme, more than 10 Gbit of raw data were tested with the parameter n set to 3. The raw data sequence at three different frequencies corresponds to the data shown in Fig. 4(a). . Static test Ideal value 1 MHz 100 kHz 10 kH Entropy 1 1 0.9999 0.99999 Mean value 0.5 0.4997 0.5057 0.4991 Chi-square 5%–95% 23% 65% 33.93% Monte Carlo value π 3.1459 3.1500 3.1423 Serial correlation 0 0.0011 0.0167 0.0011 Results pass pass pass pass

Table 1. The standard statistical test of ENT. For each scheme, more than 10 Gbit of raw data were tested with the parameter n set to 3. The raw data sequence at three different frequencies corresponds to the data shown in Fig. 4(a). .

In summary, we have designed a scheme for a hybrid random number generator based on the arrival time of photons, which combines multiple random number sources. We have experimentally verified the randomness of the sequences for every step. Compared to our previous QRNG design, which was based on time intervals, the randomness has improved dramatically and the random sequence is almost uniformly distributed. Moreover, with the help of MCA and ENT methods, the scheme has been tested both qualitatively and quantitatively. With the utilization of multiple random number sources, our schemes demonstrate excellent efficiency, which makes QRNG suitable for various circumstances. More importantly, by using a hybrid-type scheme, existing low-efficiency schemes can be profitably used to generate high-efficiency QRNGs.