Information theory provides a constructive criterion for building probability distributions based on partial knowledge, and prospers a kind of statistical subject which is called the maximum-entropy estimation.^[1] Information entropy proposed by Shannon to measure the uncertainty has become a universal concept of statistical physics.^[2] Information capacity is shown to be equal to the supremum over all processes of the input–output information rate. It is defined as the limiting information rate (in units of information per unit time) that can be achieved with arbitrarily small error probability.^[3]

Multiple-input multiple-output (MIMO) technology has been used for increasing the channel capacity and information transmission rate, and has been widely investigated in cooperative communication,^[4] wireless sensor networks,^[5,6] terahertz communication systems,^[7] fuzzy systems,^[8] etc.

The application of time reversal (TR) was demonstrated first in acoustics detection, and then it was introduced into electromagnetics^[9] and now it has been widely adopted in subwavelength focusing, super-resolution imaging,^[10–12] and MIMO wireless communication.^[13] With inherent spatial–temporal focusing property, TR can compress channel delay spread and alleviate inter-symbol interference which promotes itself as an ideal candidate in wideband or ultra-wideband communication.^[14,15] Moreover, TR is a perfect paradigm for green wireless communication by exploiting the multi-path propagation from the surrounding environment.^[16] Referring to the channels in the TR MIMO system, they often default for statistical uncorrelation. However, in realistic circumstances, the statistical correlation of channels caused by antenna mutual coupling will probably exist.^[17]

Antenna mutual coupling will change the antenna radiation patterns and electrical current distribution. Two contradictory conclusions have been drawn from these research works about mutual coupling. One conclusion is that the induced radiation pattern caused by mutual coupling with reduced antenna separation may induce angle diversity: this may provide a new dimension for MIMO communication with improved power collection capability.^[18] Another contradictory conclusion is that the channel correlation which is excited by mutual coupling will worsen the ill condition of the channel matrix. In this manner, antenna mutual coupling will become detrimental to systematic information capacity.^[19]

In wideband TR MIMO system, the TR technique is to pre-code the information symbols with the conjugated and transposed channel information before transmission. The symbols can be viewed as experiencing an equivalent stochastic channel whose response is the convolution of the original propagating channel and its conjugate transposition.^[20] Thus, traditional channel capacity of MIMO system is correlated with the eigenvalue of the MIMO channel matrix,^[21] while the information capacity of TR MIMO system relates to the square of the eigenvalue of the channel matrix. Thus the different relationships with eigenvalues of the propagating channel matrix in MIMO system invoke our research with or without using TR. To our knowledge, it is the first time that the channel statistical correlation caused by antenna mutual coupling in wideband TR MIMO system has been investigated.

In this paper, we first derive the whole symbol transmission process in wideband TR MIMO system. Then the mutual impedances are calculated for dipoles with different distances. The wideband channels are divided into frequency flat sub-channels, and the corresponding correlation coefficient is calculated in each sub-channel based on the self- and mutual impedances of dipoles. Channel capacities are derived based on the correlation coefficients in each sub-channel combined with the statistically independent wideband Rayleigh channel.^[22] It can be concluded that mutual coupling reduces the channel capacity slightly, but it makes the channel capacity steady in a small range, while the channel capacity with the wideband Rayleigh channel is distributed in a larger range which presents greater randomness and depends on the channel condition. This work provides a method of designing relatively optimal wideband TR MIMO system according to specific channels in realistic communications.

The rest of this paper is organized as follows. In Section 2 the wideband TR MIMO system and its computation method of information capacity are presented. In Section 3, the self- and mutual impedance matrix of dipole antennas are calculated by the CST Microwave Studio, then correlation coefficient matrix and channel matrix are calculated accordingly in each sub-channel, subsequently the channel capacity of the entire wideband TR system are computed. In Section 4 the results are analyzed. In Section 5 some conclusions are drawn from the present investigation.

Throughout this paper, we use the following notations: bold uppercase (lowercase) letters indicate the matrices (row or column vector); (·)^T, (·)*, (·)^H, and (·)⁻¹ denote the matrix transpose, conjugate without transpose, conjugate transpose, and inverse matrix respectively.

The TR has gained plenteous attention in wireless communications. Apart from coping with the large delay spread of wideband or ultra-wideband channel thus mitigating inter-symbol interference,^[23] it can also achieve better performance with lower transmitted power and increase the channel capacity tremendously.

2.1. Wideband data links

In this paper, wideband multipath channel and the sampled channel model can be expressed as

where L is the longest time delay length, h_l is the amplitude of the l-th path, and T_s is the sampled time interval. Then the time reversed pre-coding sequence is^[20]

Obviously, the range of the variable k is k= 0,1,…,L.

In the MIMO system, assuming there are M_t transmitting antennas and M_r receiving antennas, then we can use M_r × M_t dimension matrix H[l(l= 0,1,…,L − 1)] to represent the channel, where L is the longest delay length among all of M_r × M_t SISO communication links. The channel impulse response between the i-th receiver antenna and j-th transmitter antenna is h_{i j} [l] (i= 1,2,…,M_r, j= 1,2,…,M_t).

At the k-th moment, (M_r × 1)–dimensional receiving signal vector y[k] can be denoted as

where

E_s is the total symbol energy, n[k] is the M_r × 1 noise vector at moment k and is expressed as

On all the M_t transmitting antennas, the transmitted symbol vector after TR precoding at moment k is

Obviously, . Then we can express the j-th transmitting signal vector in Eq. (2) as

Here we use S to indicate the symbol matrix before time reversed pre-coding in Eq. (5). The symbol vector expression before TR operation in Eq. (5) can be denoted as

Thus, transmitting symbol matrix S can be described as

Using column vector g_j to denote the j-th row vector of the left multiplication matrix in Eq. (5), that is, g_j = [g_j,1 g_j,2 … g_j,Mr]^T, j = 1,2,…,M_t, and substituting Eqs. (5) and (6) into Eq. (2), we have

By successive matrix multiplication, it can eventually be obtained that each receiving antenna has its corresponding maximal received signal flow (i.e. the i-th symbol flow has a maximal signal intensity on the i-th receiving antenna). On the condition that continuous P symbols are detected on all the receiving antennas, each receiving antenna will receive continuous maximal P symbols of its corresponding symbol flow, although the P symbols are accompanied by many interfering symbols of other moments.

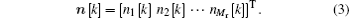
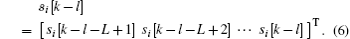
From the MIMO data link expressions, we can see that each data flow is the total channel effect of the corresponding receiver antenna to all the transmitter antennas. Then each signal flow on the corresponding antenna can be detected by a decision threshold, thus omitting the complex channel equalization process.^[15]

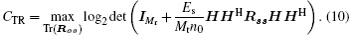
According to circuit theory, the correlation coefficient matrix R_Tx at transmitters and R_Rx at receivers can be obtained as^[24]

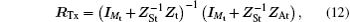
Although the Kronecker channel model has many deficiencies, it is still applicable to the situation where antenna number is small and the signal-to-noise ratio (SNR) is low. Hence, the number of dipoles and the SNR are both small in all of our capacity simulations. In this regard, the Kronecker model fits our research very well.^[25,26] In the Kronecker model, the correlation channel can be expressed by the separated correlation properties of both link ends

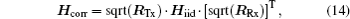
Substituting Eq. (14) into Eq. (11), the channel capacity of coupled wideband TR system can be derived as^[21,27]

Applying singular value decomposition to each sub-channel matrix, , where Λ_n = diag(λ_n,1,λ_n,2,…,λ_n,r) represents the diagonal matrix composed of singular values of each sub-channel matrix, and r is the corresponding maximal number of matrix rank among all sub-channels. Then equation (15) can be turned into

In this section, all the simulation results are presented about how antenna mutual coupling affects the information capacity of TR MIMO wideband system. First we consider a 2 × 2 MIMO system. The simulations are implemented by using the following parameter values: all antennas are parallel dipole antennas, the working frequency band of dipole is 2.8–3.15 GHz, the central frequency is 3 GHz, and λ is the central wavelength. All the impedance values are calculated by the CST Microwave Studio.

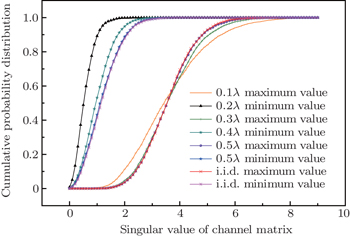
Figure 1 shows the correlation coefficients calculated by the values of self- and mutual impedances at a frequency of 3 GHz. We change the normalized distance (taking λ as a reference value) between two parallel dipole antennas, then calculate the self- and mutual impedances correspondingly. Finally, using these self- and mutual impedance values, we calculate the corresponding correlation coefficients according to Eqs. (12) and (13).

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. variation of the correlation coefficient of two dipoles with normalized distance at a central frequency of 3 GHz. The inset shows the variations of the real part and imaginary part of self- and mutual impedances of the two dipoles with the normalized distance. Z11 and Z12 are the self- and mutual impedance values of the two parallel correspondingly.

In Fig. 2, the variations of the correlation coefficient with frequency in the operating frequency range of two parallel dipoles are described. The normalized distance between two parallel dipoles varies from 0.1λ to 0.8λ in steps of 0.1λ. Apparently, due to the fact that the match degree between the dipole impedance and excitation source varies in the whole working frequency bandwidth, the correlation coefficient of two parallel dipoles changes with normalized distance in the whole bandwidth. The two parallel dipoles with 0.1λ normalized distance have large correlation coefficient comparatively. The dipoles with 0.2λ distance have larger correlation than those with other normalized distance values, but smaller than 0.1λ. Dipoles with other normalized distances have fluctuant correlation coefficients, but they are small as a whole. This variation is in accordance with the changing rules shown in Fig. 1.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Variations of correlation coefficient with frequency of two dipoles for different normalized distances.

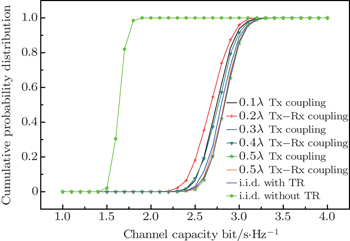
Figure 3 displays the cumulative probability distributions of the maximum and minimum singular values by decomposing the 2 × 2 MIMO channel matrix under different conditions. The first six curves denote the maximum and minimum singular values for the cases that the normalized distances between two parallel dipoles are 0.1λ, 0.2λ, and 0.5λ, respectively. The last two curves present the maximum and minimum singular value distributions for the i.i.d. channels without coupling. From Fig. 2, two dipoles with a normalized distance 0.1λ have the largest correlation coefficient, and the ones with a normalized distance of 0.2λ have the second largest correlation coefficient. The results show that when the correlation coefficient becomes smaller, the singular value distribution turns closer to the independent channels.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Plots of cumulative probability distribution versus singular value of channel matrix in a 2 × 2 MIMO system for different maximum and minimum singular values in a 2 × 2 MIMO system, on the conditions that the normalized distances of the two dipoles are 0.1λ, 0.2λ and 0.5λ at both ends respectively and the last two conditions correspond to the i.i.d. channels without coupling at both ends.

The cumulative probability distributions of channel capacity with a 2 × 2 MIMO system in several different cases are shown in Fig. 4. All capacity simulations in this paper are on the condition that SNR is 0 dB. Here, 0.1λ Tx coupling means that the distance between transmitting dipoles is 0.1λ, while the receiving dipoles are assumed to be ideally independent without coupling. Comparatively, 0.1λ Tx–Rx coupling indicates that both transmitting and receiving dipoles are 0.1λ apart. The 0.2λ and 0.5λ cases have similar meanings. Moreover, i.i.d. with TR denotes the 2 × 2 MIMO system with independent Rayleigh channels combining with TR technology. Conversely, i.i.d. without TR has the same meaning except for using the TR method.

Fig. 4.

Figure Option ViewDownloadNew Window

Fig. 4. Plots of cumulative probability distribution versus channel capacity in a 2 × 2 MIMO system with different normalized distances. 0.1λ is the distance between two dipoles Tx coupling indicates that the transmitting dipoles are 0.1λ apart but the receiving dipoles are independent; Tx–Rx coupling signifies that both the transmitting dipole distance and receiving dipole distance are 0.1λ. The others have the same meanings as shown elsewhere. In addition, i.i.d. with TR means independent 2 × 2 MIMO channel with TR, and i.i.d. without TR refers to independent 2 × 2 MIMO channel without TR.

The most apparent conclusion is that adopting TR in a 2 × 2 MIMO system can gain much larger capacity than in situations without TR. This is because the channel capacity of a TR MIMO system is correlated with the biquadrate of the channel singular values whereas the MIMO system without TR is just related to the square of singular values.^[19,20] When the singular values are larger than one, they contribute to the capacity increase of a TR MIMO system. Another phenomenon is that although coupling will reduce the channel capacity of TR system, its effect is very limited due to a similar reason.

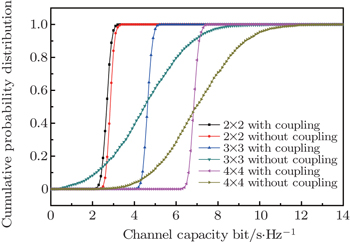
The cumulative capacity distributions of the 2 × 2 parallel dipoles with different normalized distances both at the transmitting and receiving terminals are shown in Fig. 5. The SNR in the whole simulation process is 0 dB. Obviously, the larger the correlation coefficients, the smaller the value range of the channel capacity is. The results in Fig. 5 coincide with the outcomes in Fig. 2.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Variations of cumulative probability distribution with channel capacity in a 2 × 2 MIMO system with different normalized distances.

How the capacities of the 2 × 2 parallel dipoles with different normalized distances both at the transmitting and receiving terminals change with SNR is demonstrated in Fig. 6. The variation tendency is in accordance with that in Fig. 5. Owing to the limited applicability of the Kronecker correlation channel model as we have mentioned before, the simulated range of SNR is from 0 to 8 dB.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Variations of channel capacity with SNR under different dipole configurations.

In Fig. 7, we extend our 2 × 2 system to 3 × 3 and 4 × 4 MIMO systems. The 2 × 2 MIMO system with coupling means that the distances between two dipoles at transmitter and receiver are both 0.1λ, while the 2 × 2 without coupling denotes that the simulated channels are independent Rayleigh channels. The 3 × 3 and 4 × 4 MIMO systems have just the same parameters except for the number of dipoles. Obviously, the variation range of the channel capacity in the coupled TR system is smaller than that in the TR system without coupling. In other words, the TR MIMO system with antenna mutual coupling has a more stable channel capacity distribution, i.e., the channel capacities in 3 × 3 or 4 × 4 MIMO system with TR are less susceptible to the channel condition than without TR. Here in our 3 × 3 and 4 × 4 TR MIMO systems, the capacity with coupling has about half probability larger than that without coupling.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. Plots of cumulative probability distribution versus channel capacity under different antenna combinations, i.e., 2 × 2, 3 × 3, and 4 × 4 MIMO systems with coupling at both ends or i.i.d. channels.

In this paper, the influence of antenna mutual coupling on the capacity in a wideband time reversal MIMO system combined with stochastic channels is investigated for the first time. By dividing the wideband frequency selective stochastic channel into frequency flat sub-channels, the statistical correlation coefficient matrixes related to the mutual impedance matrixes caused by antenna coupling are calculated accordingly in each sub-channel. The singular value cumulative distributions of channel matrix in different situations are compared, so are the information capacities in different MIMO communication settings. Conclusions can be summarized below. For one thing, by taking time reversal technology in a wideband MIMO system, the information capacity can be enlarged dramatically compared to the case without time reversal; for another thing, in a time reversal wideband MIMO system, channel statistic correlation caused by antenna mutual coupling stabilizes the information capacity distribution into a smaller range, which means that the mutual coupling weakens the randomness in the capacity of the channel, whereas the channel capacity with statistically independent channels is much more dependent on the channel.