Cite this Article
Zhang Yi, Ye Wen-Jun, Yuan Ping, Zhu Huan-Cheng, Yang Yang, Huang Ka-Ma. Analysis and experiments of self-injection magnetron. Chinese Physics B, 2016, 25(4): 048402  
Permissions
Analysis and experiments of self-injection magnetron
Zhang Yi, Ye Wen-Jun, Yuan Ping, Zhu Huan-Cheng, Yang Yang†, , Huang Ka-Ma
College of Electronics and Information Engineering, Sichuan University, Chengdu 610065, China

 

† Corresponding author. E-mail: yyang@scu.edu.cn

Project supported by the National Basic Research Program of China (Grant No. 2013CB328902) and the National Natural Science Foundation of China (Grant No. 61501311).

Abstract
Abstract

Magnetrons are widely used in microwave-based industrial applications, which are rapidly developing. However, the coupling between their output frequency and power as well as their wideband spectra restricts their further application. In this work, the output frequency and power of a magnetron are decoupled by self-injection. Moreover, the spectral bandwidth is narrowed, and the phase noise is reduced for most loop phase values. In order to predict the frequency variation with loop phase and injection ratio, a theoretical model based on a circuit equivalent to the magnetron is developed. Furthermore, the developed model also shows that the self-injection magnetron is stabler than the free-running magnetron and that the magnetron’s phase noise can be reduced significantly for most loop phase values. Experimental results confirm the conclusions obtained using the proposed model.

PACS: 84.40.Fe;85.40.Qx;88.80.hp;
Keyword:self-injection magnetron;frequency and power decoupling;feedback loop;noise reduction;
1. Introduction

Nowadays, many microwave-based industrial applications are rapidly developing, such as plasma and microwave chemical vapor deposition, which require high intensive electromagnetic fields.[1,2] Meanwhile, microwave wireless power transmission systems and space solar power satellite/station systems need high continuous microwave power.[3–7] The energies of single microwave sources can hardly meet these demands. An attractive method of generating high continuous microwave power is coherent, magnetron-based power-combination since magnetrons are low-cost and highly efficient.[3–5] However, the coupling between a magnetron’s output frequency and power presents one of the significant obstacles to coherent power-combination, because both the frequency and power vary with the anode current of the magnetron. Hence, it is difficult to adjust each magnetron to exactly the same frequency and power to achieve a high combined efficiency.[8–10] On the other hand, free-running magnetrons produce wideband spectra with high noise, restricting the applications of magnetrons in communications and other scientific fields.[11]

The conventional methods of addressing the coupling between the output frequency and power as well as reducing the noise of the free-running magnetron spectra include external-injection locking, power supply system improvement, and the combination of these two techniques.[6,11–16] Usually, external-injection locking can lock the output frequency of a magnetron at the injection frequency, thus improving the phase noise. However, the locking bandwidth depends greatly on the injection ratio. Therefore, expensive solid-state drivers are required to achieve wide locking bandwidths for high-power magnetrons.[12–15] Furthermore, the power supply system also significantly affects the output performance of a magnetron. Therefore, previous researchers also studied the combination of external-injection locking and using an improved power supply system to reduce the injection ratio and to improve the noise performance.[6,11] However, all these systems contain microwave active circuits, and thus are costly and fragile.

In this study, we develop a novel way of controlling a magnetron’s output frequency and power individually by introducing a feedback loop, which contains no microwave active device. Moreover, the output spectrum of the self-injection magnetron is narrowed, and the phase noise is reduced for most loop phase values. In order to predict the frequency variation with loop phase and injection ratio, a theoretical model based on a circuit equivalent to a magnetron is developed. Numerical analysis indicates that the frequency variation with loop phase can be approximated by a sine curve with a stretched declining region and a compressed rising region. Furthermore, the self-injection magnetron is found to be more stable than the free-running magnetron except that the loop phase is around (2k + 1)π. The phase noise is also reduced when the magnetron is stabler. Experimental results demonstrate that the frequency of the self-injection magnetron changes with loop phase, while the output power remains steady under a stable anode current. The spectral bandwidth of the self-injection magnetron is also narrowed for most loop phase values except for π and 5π/4. The phase noise in the narrowed spectra is also reduced compared with that of a free-running magnetron spectra. The experimental results well match the theoretical predictions.

The rest of this paper is organized as follows. In Section 2, the relation between frequency and noise performance of the self-injection magnetron is obtained based on the equivalent circuit model. Numerical analyses are also performed to investigate the effects of loop phase and injection ratio on the frequency and noise performance in this section. Experiments are carried out to test the theoretical predictions. The experimental system is depicted in Section 3. The experimental results as well as their comparison with the theoretical predictions are discussed in Section 4. Finally, some conclusions are drawn from the present investigation in Section 5.

2. Theoretical analysis
2.1. Frequency and power decoupling

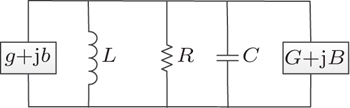
The equivalent circuit model for the magnetron which has the pulling and pushing effects is shown in Fig. 1.[12] The resonant cavity of a magnetron can be equivalent to an RLC circuit. The electron interaction in the cavity is represented by electronic conductance g and electronic susceptance b. The characteristic of the load is equivalent to the load conductance G and load susceptance B.

Fig. 1. Equivalent circuit model of magnetron.

The oscillation equation of the circuit is shown as

where is the resonance frequency of the unloaded cavity and Qext is the quality factor of the external load. When the magnetron is operated with an injection signal, the equation of the injected magnetron can be written as[12]

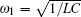
Therefore, the phase differential equation of an injection magnetron can be obtained from Eqs. (1) and (2) as follows:[12]

where ωi and ωf are the frequencies of the injection signal and the free running magnetron, respectively, θ is the phase difference between the injection signal and the magnetron output and denotes the injection ratio.[12]

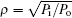
For a self-injection magnetron, the injection signal is just a portion of the output of the magnetron itself. Therefore, the injection frequency ωi is exactly the same as the output frequency ωout of the magnetron. Moreover, θ always remains constant in the steady state. Hence, the steady-state equation of a self-injection magnetron can be expressed as follows:

Equation (4) indicates that the output frequency is related to the phase delay of the feedback loop. Besides, the equations derived above are independent of the anode current.[17] Furthermore, the output power of a magnetron is controlled by the anode current.[8] These facts guarantee, at least theoretically, the decoupling between the frequency and power by self-injection. The output power and frequency can be adjusted individually by controlling the anode current and the loop phase, respectively.

Even though the output power and frequency can be decoupled by self-injection, the detailed relationship between the output frequency and the system parameters should be studied further by using Eq. (4). Through the analyses above, it can be concluded that the frequency varies with the loop phase. In turn, the frequency variation results in further loop phase change. However, in the steady state, the loop phase can be expressed as θf(ωout/ωf), where θf and θ are the loop phases under the free-running frequency ωf and the output frequency of the self-injection magnetron ωout, respectively. Since the physical length of the feedback loop remains constant, the frequency variation can be expressed as a function of the self-injection magnetron system parameters as follows:

2.2. Noise performance

The stability of self-injection oscillators has been analyzed previously.[18] A magnetron is also a type of oscillator, and the circuit equivalent to a magnetron is the same as the analyzed parallel-resonant circuit in Ref. [18]. Therein, it was reported that the stability requirement for a self-injection parallel-resonant oscillator can be expressed as

where δ is a small fluctuation in the phase difference and θ is the loop phase value.[16]

However, it was also reported that the loop phase was assumed to be constant in the analyses and that the effects of the oscillator frequency shift and loop phase variation should be carefully studied in the future.[16] Therefore, if the frequency shift is considered, the loop phase of a self-injection magnetron in a steady state can also be expressed as θf(ωout/ωf). Then, equation (6) can be written as

which is derived from Eq. (5).

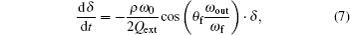
Equation (7) demonstrates the stability of a self-injection magnetron. First,

is expressed as k for convenience in the rest of the paper. If k is negative, the fluctuation δ of the phase difference between the magnetron output and the self-injection signal approaches to zero, and the phase difference is stable. Otherwise, if k is positive, δ increases with time increasing. A self-injection magnetron cannot stabilize its phase nor frequency under this condition. The numerical analyses of k as a function of loop phase and injection ratio are presented in Subsection 2.3, Figs. 3 and 5.

The phase noise is the ensemble average of the phase fluctuation power spectral density. With small phase fluctuation, the phase noise will be low.[18,19] To further analyze the relationship between the phase noise of a free-running magnetron and a self-injection magnetron, Bn(t) is introduced to represent the time-varying noise susceptance.[19] Then the equation of the self-injection magnetron with noise can be described as

where φout and φinj are the instantaneous phases of the output signal and injection signal of magnetron, respectively.

Assuming that the noise is a small perturbation to a noise-free solution, we can write

where the quantity with the symbol hat ̂ is a steady-state quantity, the δφout(t) and δφinj(t) describe the small phase fluctuations of the output and injection signal of the magnetron, respectively. Moreover, it is reported that the relationship can be expressed as[19]

where * is the convolution symbol, h(t) is the time-domain transfer function of the feedback loop, and H(ω) is its frequency-domain transfer function. For the self-injection magnetron, the feedback loop just delays the output signal. Therefore, H(ω) can be described as e−jωTfd, where Tfd is the loop delay time and can be calculated from θf/ωf.[19] Then equation (8) can be expressed as

where is the steady state phase delay of the feedback loop, which can be described as θf (ωout/ωf).

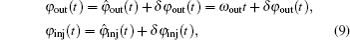
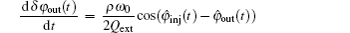
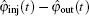
To convert the time-domain phase fluctuations into a frequency-domain phase noise, we can perform the Fourier transform of Eq. (11) as

where ωm is the offset frequency and the tilde (˜) denotes a transformed variable.

The power spectrum of the magnetrons phase fluctuation is calculated from , where the notation 〈 〉 represents an ensemble average. Besides, the results of are the same as the results of . Moreover, in the absence of the self-injection signal (ρ = 0), derived from Eq. (12) is the phase noise of the free-running magnetron, which is represented as . Then the relationship between the phase noise of the self-injection magnetron and that of the free-running magnetron can be expressed as

In previous studies, to conduct theoretical analyses, the output frequency ωout was approximated as being equal to the free-running frequency ωf of the oscillator, and the loop phase was also approximated as a constant. The previous researchers stated in the conclusions that the frequency shift and loop phase variation should be carefully studied in the future.[19] If equation (13) is solved numerically using the output frequency derived from Eq. (5), accurate analyses can be performed. The numerical results and discussion are given in Subsection 2.3 and Fig. 6.

2.3. Numerical analysis

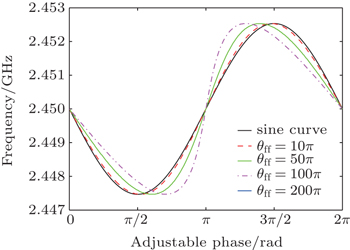
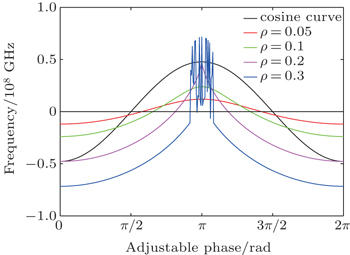
Equation (5) shows the relationship between the output frequency and the system parameters such as the loop phase and injection ratio. To investigate the effect of the feedback loop length on the output frequency, the loop phase can be split into a fixed part and an adjustable part θfa, i.e., θf = θff + θfa. Here, the phase of the coaxial cable and the waveguide in the feedback loop, and the phase shift in the feedback loop are represented. The numerical results are shown in Figs. 2 and 3, which are obtained using a free-running frequency of 2.45 GHz and a frequency tuning bandwidth of 10 MHz for a power injection ratio of 0.1.[14,17,20,21]

Fig. 2. Frequency variations with adjustable phase for different loop phases.

The frequency variation with adjustable loop phase θfa can be approximated by a sine curve with a stretched declining region and a compressed rising region as shown in Fig. 2. The width of the rising region becomes smaller as θff increases from π to 100π. Moreover, if the fixed feedback loop exceeds 200λf, the frequency starts to fluctuate. The frequency fluctuation indicates that the magnetron is not very stable in this case. In Fig. 2, the fluctuations occur when the adjustable loop phase is nearly π, which is in accordance with the result of the magnetron stability analysis and will be discussed in detail later.

Figure 3 shows the frequency variation with adjustable phase for different injection ratios. The frequency tuning bandwidth increases with injection ratio increasing. Moreover, the rising regions become more compressed as the injection ratio increases. Again, frequency fluctuations appear near an adjustable loop phase value of π.

Fig. 3. Frequency variations with phase for different injection ratios.

The stability of a self-injection magnetron is described by Eq. (7), which shows that a self-injection magnetron is stabler if k is negative. The numerical results for the coefficient k are shown in Figs. 4 and 5. In the previous analysis, the output frequency of the self-injection magnetron is approximately the same as that of a free-running magnetron, and the loop phase is also assumed to be constant.[18] Therefore, the variations of k with adjustable loop phase exhibit cosine function shapes as shown in Figs. 4 and 5. With considering the frequency shift and the loop phase variation, the range of the negative k values is found to be larger than π.

Figure 4 shows the variations of the coefficient k with loop phase. As the fixed loop phase increases from 10π to 200π, the range of the negative k values widens. Fluctuations also appear when the fixed loop phase reaches 200π because of the frequency fluctuations.

Fig. 4. Variations of k with adjustable phase loop phase for different values of θf (k < 0: noise reduced).

Figure 5 shows the variations of the coefficient k with adjustable phase for different injection ratios. As the injection ratio increases from 0.05 to 0.3, the range of the negative k widens. Fluctuations also appear when the injection ratio reaches 0.3 because of the frequency fluctuations.

Fig. 5. Variations of k with adjustable phase for different injection ratios (k < 0: noise reduced).

Figures 4 and 5 demonstrate that a self-injection magnetron cannot be stabilized if the adjustable loop phase approaches to zero because of the positive k value, which is in accordance with the previous parallel resonant oscillator analysis results.[18] Moreover, with the increase of total loop length or injection ratio, the range of the negative k values widens. Nevertheless, certain limitations are necessary on the total loop length and the injection ratio, because if the feedback loop is too long or the injection ratio is too large, the output frequency will fluctuate, and frequency fluctuations may result in positive k values. In addition, longer loops cause higher insertion losses, which is also inadvisable in practice.

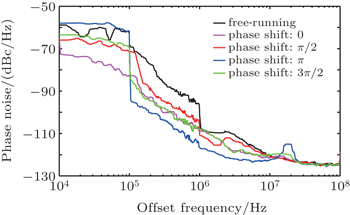
The phase noise of a magnetron is closely related to its stability. With increasing magnetron stability, the fluctuation of the phase difference between the magnetron output and self-injection signal approaches to zero, and the phase noise decreases. Moreover, the relationship between the phase noise of a self-injection magnetron and a free-running magnetron is described in Eq. (13), and the numerical results are shown in Fig. 6.

Fig. 6. Plots of phase noises versus offset frequency for free-running magnetron and different θfa values of self-injection magnetrons.

The spectral characteristics of the phase noise in a self-injection magnetron are shown in Fig. 6. The free-running magnetron phase noise follows the ideal 1/f2 dependence. As the adjustable loop phase increases from 0 to 3π/2, the phase noise decreases at low offset frequencies except that the adjustable loop phase is π. For the self-injection magnetron with an adjustable loop phase of π, a peak occurs in the phase noise. Meanwhile, at high offset frequencies, the phase noise of the self-injection magnetron is the same as that of the free-running magnetron. With considering the frequency shift and loop phase variation, the loop phase range in which the phase noise can be reduced becomes larger than those presented in previous reports in which frequency shift and loop phase variations were ignored.

3. Self-injection magnetron experimental setup

The experimental system of the self-injection magnetron is depicted in Fig. 7. The test magnetron was a Panasonic CW magnetron 2M244-M1, which produces an output power of 1000 W around 2.45 GHz with an anode current of 350 mA. The injection power was coupled by a 10-dB directive coupler and adjusted by an attenuator. The majority of the output power was absorbed by water load1. The two circulators separated the injection power from the reflection power. The separated reflection power was absorbed by load2. Therefore, the injection power could also be measured using the directive coupler. The loop phase was adjusted by a phase shifter placed in the feedback loop that could adjust the phase from 0 to 5π/2 in intervals of π/4 at a frequency of 2.45 GHz. A coaxial cable with a power capacity of 150 W connects the coupled port to the injection port.

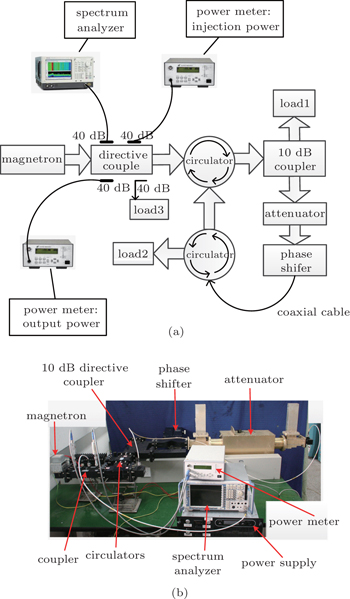Fig. 7. (a) Experimental setup of self-injection magnetron system, and (b) photograph of experimental self-injection system.

The output spectrum and power were coupled by a double directive coupler and measured by a Tek RSA6100B spectrum analyzer and an AV2433 power meter, respectively. The RSA6000 Series provides the functionality of a high-performance spectrum analyzer, wideband vector signal analyzer, and the unique trigger-capture-analyze capability of a real-time spectrum analyzer all in a single package. The DPX spectrum of the Tek RSA6100B spectrum analyzer provides an intuitive understanding of time-varying RF signals with color-graded displays based on frequency of occurrence.[22]

4. Results and discussion

To measure the output frequency and power as well as noise performance of the free-running magnetron, the injection port and the output port of the phase shifter are terminated with matched loads. The variations of output frequency and power with the anode current are shown in Fig. 8. Obviously, both the output frequency and power increase with anode current. The output frequency increases by 11 MHz and the output power increases from 427 W to 1000 W as the anode current increases from 170 mA to 370 mA.

Fig. 8. Variations of frequency and power with anode current in free-running magnetron.

To measure the performances of the self-injection magnetron, a coaxial cable was used to connect the coupled output power to the injection port. The anode current was maintained at 350 mA, while the phase shift was changed from 0 to 5π/2 in steps of π/4. The variations of frequency and power are shown in Fig. 9 for an injection power of 50 W.

Fig. 9. Variations of frequency and power with phase shift, where the power remains steady under stable anode current, while the frequency varies with the loop phase.

It is clear that frequency and power are decoupled as shown in Fig. 9. Because the frequency can be adjusted by changing the loop phase, the output power remains steady. Although the frequency tuning bandwidth reaches 19.7 MHz dramatically, the output power remains around 1020 W with a fluctuation less than ±10 W.

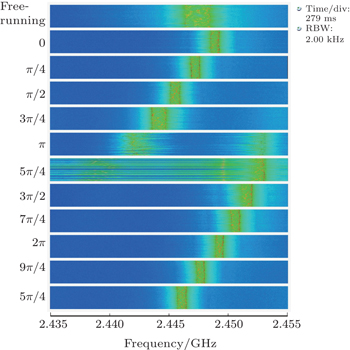
To test the theoretical frequency prediction, the theoretical frequency curve with a fixed loop phase around is shown in Fig. 9. The loop phase value is reasonable because the coaxial cable and BJ26 waveguide were about 1.5 m and 1.3 m long, respectively. Consequently, the experimental results well match the theoretical predictions. The rising region in the frequency curve is compressed, and the declining region is stretched just as indicated in Eq. (5) and Fig. 2.

The spectrogram function of the Tek RSA6100B spectrum analyzer can display the variations of frequency and amplitude with time. A spectrogram of the self-injection magnetron is shown in Fig. 10. The frequency of occurrence is color-graded, indicating the transient frequency in red and background noise in blue.[22]

Fig. 10. Spectrograms of self-injection magnetron with different phase shifts.

In Fig. 10, as the phase shift changes, it is clear that the range in which the frequency is declining turns much larger than that in which the frequency is rising. These results agree with the theoretically predicted frequency variations with loop phase. Moreover, the output frequency bandwidth of the self-injection magnetron is narrower than that of the free-running magnetron except that the phase shift is π or 5π/4. When the phase shift is π or 5π/4, the colored points appear across a wide range, indicating that the frequency has a wide bandwidth. Therefore, the self-injection magnetron is not very stable under these loop phase values.

The experimental results in Fig. 10 also confirm the theoretical predictions regarding self-injection magnetron stability. The numerical results show that the self-injection magnetron is not very stable when the loop phase is around 2kπ and that the frequency is always rising if the loop phase is increasing around 2kπ. In other words, the self-injection magnetron is unstable if the output frequency is rising with increasing loop phase, which is in accordance with the experimental results in Fig. 10. Furthermore, the phase shift range in which the magnetron is unstable is much narrower than that reported previously (π).

Fig. 11. DXP spectra of free-running and self-injection magnetrons: (a) DXP spectra of free-running magnetron, (b) DXP spectra of self-injection magnetron with phase shift of π/4, and (c) DXP spectra of self-injection magnetron with phase shift of π.

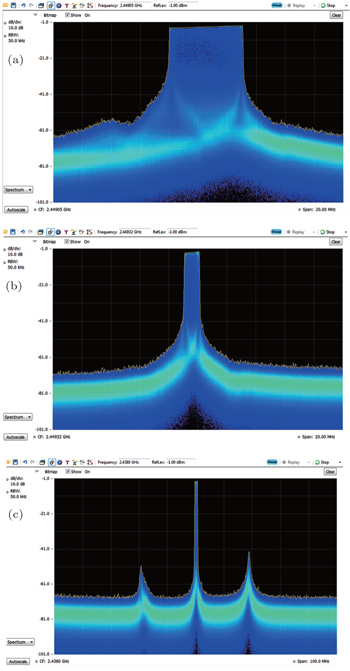
The DXP spectra of the free-running and self-injection magnetrons are compared in Fig. 11. The colored parts indicate the frequency occurrence. The center frequency and span are shown below the spectra. The free-running magnetron produces a wideband spectrum as shown in Fig. 11(a). For the self-injection magnetron, the output frequency is narrower if the magnetron is stabler as shown in Fig. 11(b). However, if the self-injection is not stabilized, the output spectrum cannot be narrowed, and the side band signal also appears at an offset frequency of approximate 20 MHz. The stability and spectral bandwidth are also closely related to the phase noise, which is shown in Fig. 12.

Figure 12 shows the plots of phase noise versus offset frequency for the free-running and self-injection magnetrons. For self-injection magnetrons with phase shifts of 0, π/2, and 3π/2, the phase noise is significantly reduced at low offset frequencies (less than 107 Hz). If the offset frequency is very high (exceeding 107 Hz), the phase noise of the self-injection magnetron is the same as that of the free-running magnetron. For the self-injection magnetron with a phase shift of π, the phase noise cannot be reduced compared with that of the free-running magnetron if the offset frequency is less than 105 Hz. Moreover, there is also a peak around an offset frequency of 20 MHz, which is similar to the DXP spectrum result. These features verify the theoretical analyses and numerical predictions.

Fig. 12. Variations of phase noise with offset frequency for free running magnetron and different phase shifts of self-injection magnetrons.
5. Conclusions

By introducing a feedback loop into a magnetron system in this study, the output frequency and power can be decoupled. The output power is controlled by the anode current, and the frequency can be adjusted by changing the loop phase. Meanwhile, the output frequency bandwidth is narrowed, and the phase noise of the self-injection magnetron is reduced for most loop phase values. Moreover, a theoretical model based on a circuit equivalent to a magnetron is developed. The frequency variation with changing loop phase can be approximated by a sine curve with a stretched declining region and a compressed rising region. Furthermore, more accurate stability and noise performance analysis are performed for a self-injection magnetron with considering the frequency shift and loop phase variation. The self-injection magnetron is stabler except that the loop phase value is around (2k + 1)π. The phase noise can also be reduced if the magnetron is stabler.

Self-injection magnetron provides the basis for a new coherent power-combining approach because it can adjust each individual magnetron to the same values of output frequency and power without external-injection locking. After the frequency of each magnetron is adjusted to the same value, the phase difference between the sources of the power-combining system can be adjusted by a pulse of biased frequency. This work is still ongoing. On the other hand, since the self-injection technique can narrow the output frequency bandwidth and reduce the magnetron phase noise, it can broaden the areas in which magnetrons can be applied to critical noise required fields such as communications and scientific fields.

Reference
1Teragi TMitani SWang CIto T 2002 J. Crystal Growth 235 287
2Hong Y CUhm H S 2006 Phys. Plasmas 13 113501
3Sasaki STanaka KMaki K I 2013 Proc. IEEE 101 1438
4Strassner BChang K 2013 Proc. IEEE 101 1379
5Matsumoto H 2002 IEEE Microw. Mag. 3 36
6Bergsrud CStraub J 2014 Acta Astronautica 103 193
7Shinohara NMatsumoto H 2010 Electr. Eng. Jpn. 173 1119
8Gilmour A S2012Klystrons, traveling wave tubes, magnetrons, crossed-field amplifiers and gyrotronsBeijingNational Defence Industry Press378334378–334
9Ha T 1980 IEE Proceedings G (Electronic Circuits and Systems) 127 148
10Chen XYu CPan WCao XZhang S 2010 High Power Laser and Particle Beams 22 2407 (in Chinese)
11Tahir IDexter ACarter R 2005 IEEE T. Electron Dev. 52 2096
12Slater J C1947 “The phasing of magnetrons” Ph. D. Dissertation (Massachusetts Institute of Technology)
13Thal H LLock R G 1965 IEEE Trans. Microwave Theory Tech. MIT-13 836
14Yue SZhang Z CGao D P 2014 Chin. Phys. 23 088402
15Yue SZhang Z CGao D P 2013 Acta Phys. Sin. 62 178401 (in Chinese)
16Chen S C 1990 IEEE T. Plasmas Sci. 18 570
17Pengvanich PNeculaes V BLau Y YGilgenbach R MJones M CWhite W MKowalczyk R D 2005 J. Appl. Phys. 98 114903
18Chang H C 2003 IEEE Trans. Microwave Theory Tech. 51 1989
19Chang H C 2003 IEEE Trans. Microwave Theory Tech. 51 1994
20Woo JBenford JFittinghoff DHarteneck BPrice DSmith RSze H 1989 J. Appl. Phys. 65 861
21Xie WMeng L1994J. Electron. Sci. Technol.23393(in Chinese)
22Tektronix LtdSpectrum Analyzers RSA6000 Series Datasheet www.tek.com