† Corresponding author. E-mail:
In this paper, the time evolution of the quantum mechanical state of a polaron is examined using the Pekar type variational method on the condition of the electric-LO-phonon strong-coupling and polar angle in RbCl triangular quantum dot. We obtain the eigenenergies, and the eigenfunctions of the ground state, and the first excited state respectively. This system in a quantum dot can be treated as a two-level quantum system qubit and the numerical calculations are performed. The effects of Shannon entropy and electric field on the polaron in the RbCl triangular quantum dot are also studied.
With the exponential advancement of nanotechnology during recent years, the study of quantum computing and quantum information processing has generated widespread interest. The two-level system is usually employed as the elementary unit for storing information. Quantum computation will be based on the laws of quantum mechanics. Several schemes have been proposed for realizing quantum computers in recent years.[1–8] Owing to the fact that quantum computers have an edge over classical computers, they will need to carry thousands of qubits. Consequently, these quantum computers with a large number of qubits will be most feasible as solid-state systems. Self-assembled quantum dots (QDs) have attracted substantial attention due to their perfect crystal structures. Therefore, they become one of the most popular solid-state quantum information research fields that qubits can be realized by solid-state devices. Many schemes with widely varying content have been proposed for carrying out research on quantum dots.[1,2,9,10] Zhores and Leo[11] gave an overview of the quantum-dot cellular automata (QCA) architecture along with a summary of the experimental demonstration of QCA devices. Sun et al.[12] reported quantitative results on the electron–phonon coupling strength in CdSe quantum dots (QDs) and rods, which were obtained by low-temperature scanning tunneling microscopy. Rozhkov and Franco[13] generalized the known solution of the Schrödinger equation, describing a particle confined to a triangular area, for a triangular graphene quantum dot with armchair-type boundaries. The quantization conditions, wave functions, and the eigenenergies were determined analytically. As an application, they calculated the corrections to the energy levels of quantum dot due to distortions of the carbon-carbon bonds at the edges of the quantum dot. Seo et al.[14] experimentally investigated the charge (isospin) frustration induced by a geometrical symmetry in a triangular triple quantum dot. They observed the ground-state charge configurations of six-fold degeneracy, the manifestation of the frustration. The frustration resulted in omnidirectional charge transport, and it was accompanied by nearby nontrivial triple degenerate states in the charge stability diagram. Their work demonstrated a unique controllable way of studying geometrical frustration. More recently, using a Modified Lee Low Pine method, Feng et al.[15] have studied the temperature effects on the excited state of a strong-coupling polaron in an asymmetric RbCl quantum dot. Sun et al.[16] have studied the temperature effects on the vibrational frequency and ground state energy of the strong-coupling polaron in symmetry RbCl quantum dots. Xiao[17] used the same method to study the effects of electric field and temperature on RbCl asymmetry quantum dot qubit. However, the joint effect of electric field and Shannon entropy on the polaron in a triangular QD has not yet been studied.
In this present work, eigenenergies of the ground state and the first-excited state, the eigenfunctions of the ground state and the first-excited state are obtained by using the variational method of the Pekar type on the condition of electric-LO phonon strong coupling in RbCl triangular quantum dot. This system in quantum dot may be employed as a two-level quantum system qubit. We obtain the probability density of the polaron which oscillates with a given period when it is in a superposition of the ground and first excited states in the presence of an electric field.
The rest of this paper has the following structure: in Section 2, we describe the Hamiltonian of the system and use the Pekar variational method to derive the energies of ground and first excited states. We also derive the density of probability and the Shannon entropy. In Section 3, we present results and discussion, and finally we draw some conclusions from the present study in Section 4.
We consider a system in which much more electrons are confined in the z direction than in the x or y direction. The electrons are assumed to be moving on the x–y plane. The confining potential is taken as the triangular bound potential form[18] and given as


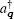
V

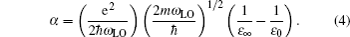
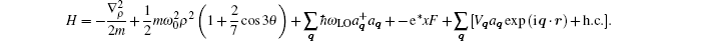
To evaluate the polaron energy, we use the Pekar variational method. To achieve our goal, we choose the trial function of strong coupling that can be separated into two parts which describe the electron and the phonon separately. The trial function cited from Ref. [19] is written as
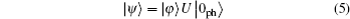
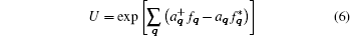

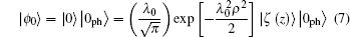
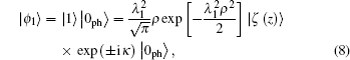

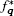
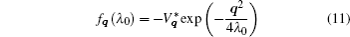

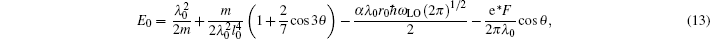
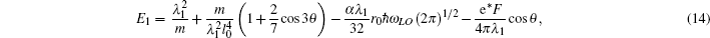




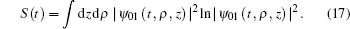
In this section we derive the numerical results of the entropy of the polaron in RbCl triangular QD. The experimental parameters used in the calculations are as follows:[20] ħωL0 = 21.45 meV, α = 3.81, and m = 0.432m0.
Figure
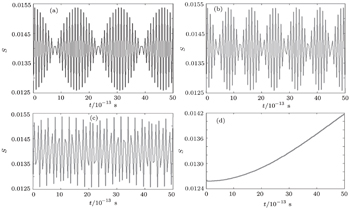 | Fig. 1. Variations of entropy as a function of time for θ = π/2, κ = 2π, l0 = 6 nm, and r = 10 nm at (a) F = 1.50 V/nm, (b) F = 10.0 V/nm, (c) F = 50.0 V/nm, and (d) F = 100.0 V/nm. |
Figure
Figure
Using the Pekar variational method, the eigenenergies and eigenfunctions of polaron in RbCl triangular QD under an electric field effect are derived. The numerical results indicate that entropy changes periodically for lower values of electric field strength and polar angle but for the higher values of electric field, the entropy increases. The increase of the entropy means the loss of information about the system; the modulation of electric field and polar angle can be carried out to control the decoherence in the system. To optimize the transmission of information, the polar angle and electric field strength need to be well modulated.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 |



