† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 51476043 and 51576053) and the Foundation for Innovative Research Groups of the National Natural Science Foundation of China (Grant No. 51421063).
An inverse estimation method and corresponding measurement system are developed to measure the apparent spectral directional emissivities of semitransparent materials. The normal spectral emissivity and transmissivity serve as input for the inverse analysis. Consequently, the refractive index and absorption coefficient of the semitransparent material could be retrieved by using the pseudo source adding method as the forward method and the stochastic particle swarm optimization algorithm as the inverse method. Finally, the arbitrary apparent spectral directional emissivity of semitransparent material is estimated by using the pseudo source adding method given the retrieval refractive index and absorption coefficient. The present system has the advantage of a simple experimental structure, high accuracy, and excellent capability to measure the emissivity in an arbitrary direction. Furthermore, the apparent spectral directional emissivity of sapphire at 773 K is measured by using this system in a spectral range of 3 μm–12 μm and a viewing range of 0°–90°. The present method paves the way for a new directional spectral emissivity measurement strategy.
The emissivity is defined as the ratio between the amount of radiation emitted by an object and that emitted by a perfect blackbody, at the same temperature and under the same geometrical and spectral conditions.[1] As a fundamental optical property, the emissivity of a material is usually strongly dependent on wavelength. As a relative physical parameter that defines the way an object emits thermal electromagnetic radiation,[2] the spectral emissivity plays an essential role in temperature measurements using radiation thermometers and in the analysis of the radiative heat transfer between objects.[3] Moreover, the spectral emissivity is highly influenced by the surface state, and depends on surface material geometry (i.e., curvature and roughness), material composition, oxidation, surface contamination, impurity, coating, thermal uniformity, etc. In other words, the spectral emissivity is a multivariate function of such factors. In particular, for a semitransparent material, due to the volumetric absorbing and scattering characteristics, the emissivity of semitransparent material is an apparent physical quantity, which strongly depends on the thickness of material and the above influence factors, and needs special consideration.
For emissivity as an important physical parameter that represents the radiative capability of materials, its accurate behavior in a wide range of wavelength and direction is of particular interest and indispensable to many applications such as remote sensing, solar energy utilization, and high-temperature measurements.[4–14] Taking non-contact high-temperature measurement (pyrometry) for example, accurate knowledge of the emissivity is required to evaluate the true temperature of a sample from the so-called radiance temperature. Uncertainty in the emissivity is the principal source of errors in determining the surface temperature from the infrared radiation measurements. Therefore, the first and most essential stage in solving the non-contact temperature measurement problems is to determine the spectral emissivity of the material accurately. In recent years, the semitransparent optical window materials, such as quartz, sapphire, zinc sulfide (ZnS), or silicon, ceramic, and inorganic composite materials, have attracted significant attention for their wide potential applications in solar heat receiver, spacecraft photoelectric detection, high-temperature measurement technology, and thermophotovoltaic applications.[5–8] The spectral emissivity values of these semitransparent materials are fundamental data of engineering design and the analyses of thermal processes and radiative transfers, which have important implications for the development of relevant engineering technology and scientific research.[9] Until now, accurate determination of the directional spectral emissivity of these semitransparent materials is still an open problem.
To accurately measure the spectral emissivity values of various materials, much effort has been made in the past several decades. Typically, the emissivity measurement approaches can be classified as two main types, namely the indirect or direct method.[15,16] The indirect measurement method is based on the measurements of other quantities related to emissivity, and these quantities can be calorimetric or radiometric. For instance, Worthing et al.[4] developed the simplest steady-state calorimetry (the filament heating method) for measuring the full wavelength hemispherical emissivity. This method however can only measure the full spectrum hemispherical emissivity.[4] Cezairliyan and Laylor[10] first established the pulse heating transient calorimetric device based on the integrating sphere reflectometry method for measuring eight thermal physical property parameters including the emissivity. Fu et al.[17] and Fu and Tan[18] developed two types of total hemispherical emissivity devices for conductive materials based on steady-state calorimetry and transient calorimetry, respectively. Consequently, the influences of surface condition, including surface roughness and oxidation state, on the total hemispherical emissivity were investigated by using improved steady-state calorimetry for iron-based alloy samples.[19] Moreover, they also developed a new method to simultaneously measure the total hemispherical emissivity and the thermal conductivity of a sample at high temperature by using steady-state calorimetry.[20] For direct measurement, emissivity is determined by comparing the emission from a sample with that from a blackbody at the same temperature and wavelength, both emissions are measured with the same detector over an identical or equivalent optical path. Since the 1990s, with the development and wide use of the Fourier transform infrared (FTIR) spectrometer, many researchers have used it to directly measure the emissivities. Lindermeir et al.[21] and Tank[22] employed the FTIR spectrometer in a direct measurement device which could measure the emissivities and temperatures of opaque materials simultaneously. The measured spectral range however is 1.3 μm–5.4 μm, the measured temperature is less than 500 K, and the maximum resolution of the spectrometer is 0.5 cm−1. Obviously, these device ranges are quite limited. Subsequently, Dai et al.[23] developed a direct measurement system of spectral emissivity, which was incorporated into an FTIR spectrometer, and extended the measured spectral range and temperature range significantly. The measurement spectral range reaches 0.6 μm–25 μm, and the measured temperature range is 333 K–1773 K.
Most of the emissivity measurement technologies introduced above are limited to opaque materials because the radiation from opaque material is only surface radiation and easily measured accurately. More recently, with the development of optical measurement and materials science, the emissivity measurements of semitransparent materials have become more and more urgent. Rigorous analyses of their radiation behaviors are hampered due to the lack of accurate values of the directional spectral emissivity. For instance, Sova et al.[24] developed a vacuum emissivity measurement device for semitransparent materials. A carbon dioxide laser was used to heat samples and the FTIR spectrometer was applied to measure the spectral radiant energy. The two-color pyrometer was used to measure the temperature of the sample. The spectral normal emissivity values of sapphire, spinel, yttria, and fused silica over the range 600 K–2000 K were measured with this device in a wave number range of 500 cm−1–5000 cm−1. González–Fernández et al.[25] used a highly accurate homemade infrared radiometer to measure the spectral normal emissivity values of atmospheric plasma sprayed (PS) YSZ films layered on Inconel 718 substrates at 603 K–1003 K based on the direct method, and the spectral range is 2.5 μm–22 μm. Rozenbaum and Meneses[26] developed a spectral directional emissivity measurement device by using a carbon dioxide laser to heat semitransparent samples. The temperatures of the samples could reach 3000 K, and the wave number range is 10–12000 cm−1. The viewing direction of the measured directional emissivity by this device was limited to a range from the normal to 60°. Lee et al.[27] developed a two-substrate method to measure the spectral directional emissivity values of semitransparent materials based on the FTIR spectrometer, and the spectral directional emissivity of alumina. However, the viewing direction was limited within a range from the normal to 50°.
In summary, most of the current emissivity measurement techniques focused on dealing with opaque materials, and most of the experimental devices could only measure the normal emissivity values. To the best of our knowledge, only a few experimental investigations have been reported on the spectral directional emissivity measurement technology for semitransparent materials. However, the existing spectral directional emissivity measurement technology for semitransparent materials is disadvantaged by limited measuring view scope and complex experimental assemblies. The directional spectral emissivities of semitransparent materials have not been thoroughly investigated and a systematic study of the directional spectral emissivity as a function of the temperature has not been found either. With this idea, the main purpose of the present work is to develop an accurate measurement technique to determine the apparent spectral directional emissivities of semitransparent materials by combining the normal spectral emissivity measurement technique for semitransparent materials with an inverse estimation method. This technique has the advantages of simple structure, high accuracy, and the excellent capability to measure the emissivity in an arbitrary direction, so that it can be widely used to measure the apparent spectral directional emissivities of various semitransparent materials. The remainder of the present study is organized as follows. The measurement principle and devices are described in Section 2. The measurement system is verified in Section 3. The apparent spectral directional emissivity measurement results of sapphire are analyzed in Section 4. In Section 5, the main conclusions are given.
To measure the arbitrary directional spectral emissivities of semitransparent materials accurately, an inverse estimation method and the corresponding measurement system are developed. The whole technical procedure can be summarized as follows. Initially, the apparent normal spectral emissivity ε⊥(λ,T) and transmissivity τ (λ,T) of the sample at the required temperature T are measured by the normal spectral emissivity measurement device. Then, with the measured emissivity and transmissivity data, the refractive index n(λ,T) and absorption coefficient κ (λ,T) of the sample are retrieved by using the pseudo source adding (PSAD) method as the direct method and the stochastic particle swarm optimization (SPSO) algorithm as the inverse method. Finally, the apparent spectral directional emissivity of the semitransparent material is predicted by the PSAD method with the input of the retrieval refractive index and absorption coefficient. In this measurement system, the measurement temperature is in a range of 300 K–1773 K, the spectral range is 2.5 μm–25 μm, and the viewing range is 0°–90°. The detailed procedures of the present technology are as shown below.
The basic principle of emissivity measurement based on the direct method is to measure the radiation energy in the normal direction of the material itself and the radiation energy in the normal direction of a reference blackbody at the same temperature; the ratio between the two values is the apparent normal emissivity of material. However, the background radiation noise and the transmission of semitransparent material make it difficult to measure the radiation energy of material itself directly, which brings great difficulty in measuring the apparent emissivity of semitransparent material. So an apparent normal spectral emissivity measurement apparatus for semitransparent material and the corresponding correction method are developed to deduce the background radiation noise first, from which the apparent normal spectral emissivity and transmissivity can be simultaneously measured. Figure
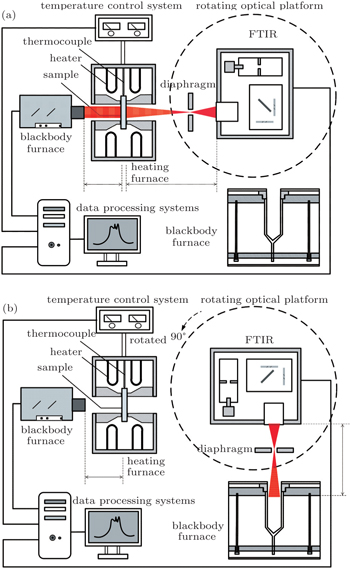 | Fig. 1. Schematic diagrams of the apparent normal emissivity measurement apparatus. (a) Radiative signal collection of the sample and (b) radiative signal collection of the blackbody. |
The emissivity measurement system is composed of an FTIR spectrometer, reference blackbody, heating furnace and its temperature control system, infrared light source, control and data processing system, and diaphragm. A standard blackbody is used for the radiometer calibration, and an FTIR spectrometer is used as a radiation detector. The furnace is heated using a silicon molybdenum heater which is controlled by a proportional-integral-derivative temperature control system. The spectrometer is fixed on an optical lift platform, which can be rotated freely from 0° to 360°. A diaphragm controls the amount of light, which is mainly used for adjusting the strength of the passing light. The high pressure mercury lamp or blackbody can be employed as an infrared source, and a high-temperature blackbody furnace is used as an infrared source in the present study. The distance between the infrared light source and the sample is L1 = 700 mm, the distance between the FTIR and the sample is L2 = 300 mm, the distance between the FTIR and the blackbody is L3 = 300 mm, the size of the heating furnace is 200 mm×200 mm×200 mm, and the diameter of the sample is 30 mm. It is worth noting that the blackbody and the sample should be viewed by the same detector over an equivalent optical path. The detailed information about the main experimental devices is listed in Table
| Table 1. Detailed information about the main experimental devices. . |
Assuming a linear response for the FTIR spectrometer to incident spectral radiance (indeed, its nonlinear response contributes to approximately 0.5% error[28] which can be approximated as a linear response), the measurement spectral radiation signal can be expressed as
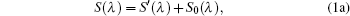
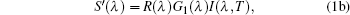
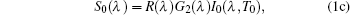
The purpose of the calibration is to determine the instrument functions G1(λ)R(λ) and G2(λ)R(λ) · I0 (λ, T0). As I(λ, T) is an essential quantity in the output signal of the FTIR spectrometer, the value of G1(λ)R(λ) is calculated from Eq. (
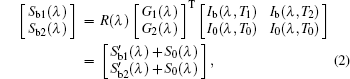
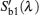
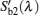
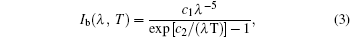
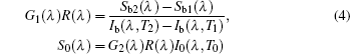
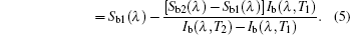
The critical problem of the apparent normal spectral emissivity and transmissivity measurement is to measure the radiative energy of the material itself in the normal direction. Therefore, the following measurement procedure is developed.
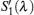
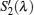
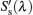
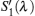
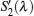
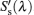
According to the above steps, the equations for the radiative signals are


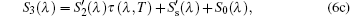
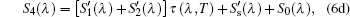
The spectral transmissivity and the real radiation signal of the semitransparent sample itself 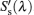
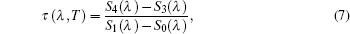

Combining Eqs. (

In addition, the spectral radiative intensity of the blackbody furnace is expressed as
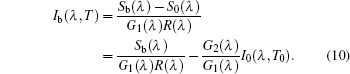
The normal spectral emissivity of the semitransparent sample without background noise interference is obtained from Eqs. (
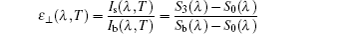

In summary, the transmissivity and apparent normal spectral emissivity of semitransparent material can be obtained according to Eqs. (
To determine the apparent spectral directional emissivity of semitransparent material, the values of the refractive index n and absorption coefficient over a wide spectral range are required to be known. In the present study, the apparent normal spectral emissivity and transmissivity measured by the measurement system serve as input for the inverse analysis. The spectral refractive indices and the absorption coefficients of the semitransparent material at different temperatures can then be retrieved by using the PSAD method as the forward method and using the SPSO algorithm as the inverse one. The apparent spectral directional emissivity of semitransparent material is then estimated by using the PSAD method with the retrieval refractive index and absorption coefficient.
The PSAD method, first developed by Huang et al.[29,30] in 1999, enables the efficient and accurate calculation of the apparent directional emissivity of semitransparent medium with known refractive index and absorption coefficient. In the present study, this method is used as the forward method to calculate the apparent spectral emissivity and transmissivity which serve as input for the inverse analysis.
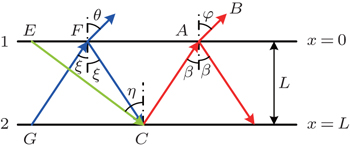
A one-dimensional non-gray semitransparent medium slab (Fig.
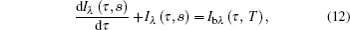
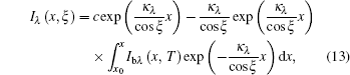
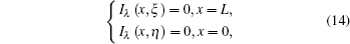
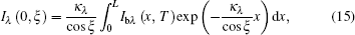
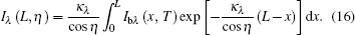
Two surface types for interface 2 are considered: one is the opaque diffuse substrate surface, and the other is the semitransparent and specular-emerging surface.
Hence the expression for the first pseudo-source intensity of a semitransparent and specular-emerging surface can be written as
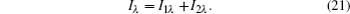
These two intensities correspond to the diffuse-light radiation, and therefore are called the first pseudo-source. The first pseudo source is transferred to the semitransparent surface after the attenuation of medium. A portion of this radiation passes to a basal surface after being reflected by a semitransparent surface, and then forms a second pseudo-source after being reflected again, and then forms a pseudo-source series. Therefore, the actual radiative intensity reaching point A along direction CA is
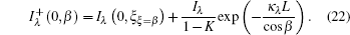
If interface 2 is an opaque diffuse substrate surface, the expression for K is
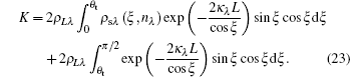
Whereas for a semitransparent and specular-emerging surface, the expression of K is written as
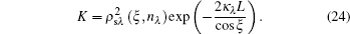
Then the spectral radiative intensity in direction ϕ corresponding to β can be written as
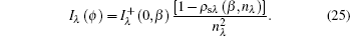
Furthermore, the apparent spectral normal radiative intensity is
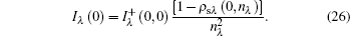
Therefore, the expression of apparent spectral normal emissivity is
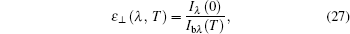
Moreover, if interface 2 is a semitransparent and specular-emerging surface, according to Beer’s law, the expression for the spectral transmissivity can be written as

The optimization method associated with the inverse problem has been a topic of great interest. It has widely developed in the past decades, and its importance in applications derives partly from the advent of large computers and reliable numerical methods. Among these methods, the Particle Swarm Optimization (PSO) algorithm, which was first developed in 1995 by Eberhart and Kennedy,[31] receives a great deal of attention due to its superior computational stability, fast solution time, and efficiency in achieving a global minimum solution compared with the conventional gradient-based methods.[32–34] Our research group has exploited several PSO-based algorithms to determine the radiative properties, particle size distributions, and geometric conditions in various inverse radiation problems. The details of the PSO-based algorithms are available in Refs. [35]–[40] and are not repeated here.
The Stochastic Particle Swarm Optimization (SPSO) algorithm, which was first developed by Zeng and Cui,[41] is a PSO algorithm which ensures the convergence of the global optimum solution with a probability of one. This algorithm has been proved to be powerful in many optimal calculations, especially in parameter estimations.[35] In the present study, the SPSO is used to determine the spectral refractive index nλ and absorption coefficient κλ. In the inverse problem, the apparent normal spectral emissivity ε⊥(λ) and transmissivity τ (λ) measured by the measurement system serve as the input for the inverse analysis to construct the objective function
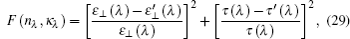
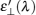
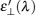
The spectral radiative intensity Iλ (θ) in direction θ can be calculated by Eq. (
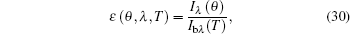
To verify the reliability of the apparent normal spectral emissivity measurement device and measurement method based on the forward method, the apparent normal spectral emissivity of the infrared-grade sapphire is measured by using the measurement device and measurement method introduced in Section 2. The diameter and thickness of the sapphire sample are 15 mm and 1.0 mm, respectively, and the test temperature is 975 K. From Fig.
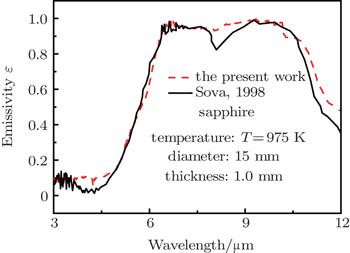 | Fig. 4. Comparison of spectral emissivity of an infrared-grade sapphire sample at high temperature (T = 975 K) between the present work and Ref. [24]. |
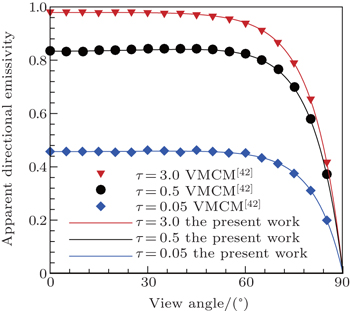
To verify the reliability of the directional emissivity solving method, the direct problem model should be verified at first, with considering a semitransparent medium (see Fig.
The inverse problem model can be verified in a numerical simulated experiment based on the forward problem model. Assume that the refractive index and absorption coefficient of the medium are known at first. Then the apparent normal emissivity and transmissivity can be predicted directly by using the PSAD method and serve as simulation experimental data for the inverse analysis. The refractive index and absorption coefficient of the medium can be retrieved by the SPSO algorithm to test the performance of the inverse method.
To demonstrate the effects of measurement errors on the retrieval results, the measured apparent normal emissivity and transmissivity with random errors are obtained by adding normal distribution errors to the exact apparent normal emissivity and transmissivity, that is,


For comparison, the relative error is defined as
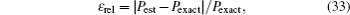
As indicated in Fig.
| Table 2. Retrieval results of absorption coefficient and refractive index. . |
Clearly from Table
Moreover, from Table
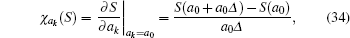
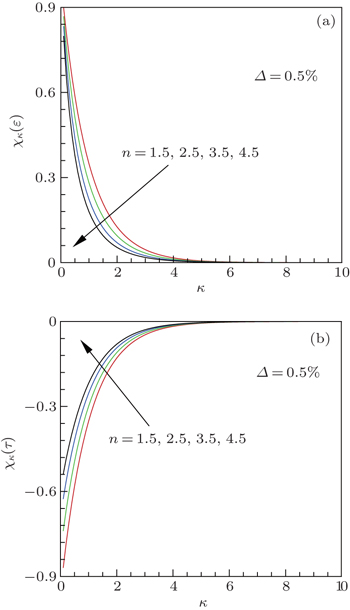 | Fig. 7. Variations of sensitivity coefficients of (a) the normal emissivity χκ (ε) and (b) transmissivity χκ (τ) with absorption coefficient κ. |
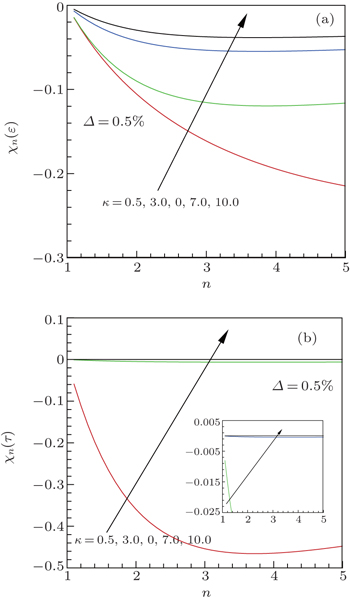 | Fig. 8. Variations of sensitivity coefficients of (a) the normal emissivity χn (ε) and (b) transmissivity χn (τ) with refractive index n. |
As shown in Fig.
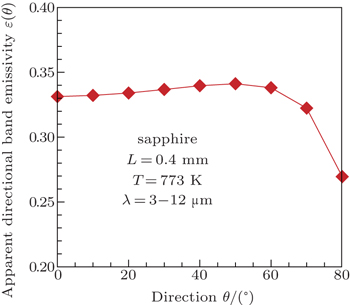
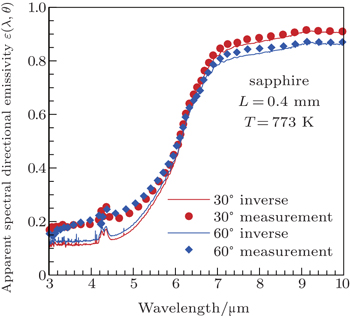
Based on the above verification, the apparent spectral directional emissivity of a sapphire sample is measured using this measurement system. The sapphire sample used in the experiment is a wafer sample, and the diameter is 50 mm, the thickness is 0.4 mm, the test temperature is 773 K, and the range of measurable wavelength is 3 μm–12 μm. The apparent normal spectral emissivity and transmissivity of this sample are measured first (see Fig.
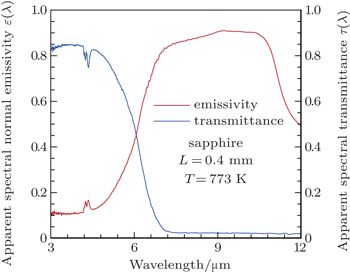 | Fig. 9. Plots of apparent normal spectral emissivity and transmissivity versus wavelength of the sapphire sample. |
According to the apparent normal spectral emissivity and transmissivity of the sample (Fig.
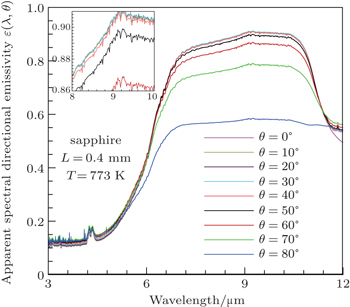 | Fig. 10. Plots of apparent spectral directional emissivity versus wavelength for different θ values of the sapphire sample. |
As shown in Fig.
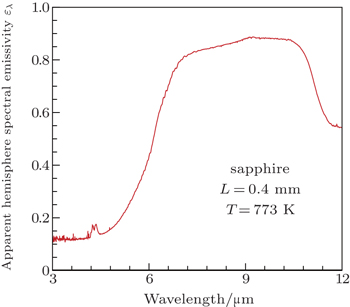 | Fig. 11. Variation of apparent spectral hemisphere emissivity with wavelength of the sapphire sample. |
In order to further verify the present inverse method, the direct measurement method is used to measure the apparent spectral directional emissivities of the same sapphire sample at the same test temperature for viewing angles 30° and 60°. A comparison between the emissivity results obtained by the proposed inverse method and the measurements is shown in Fig.
An inverse estimation method and corresponding measurement system are developed to measure the apparent spectral directional emissivities of semitransparent materials based on the direct measurement method. The apparent normal spectral emissivity and transmissivity are initially measured using the measurement system, which serves as input for the inverse analysis. The refractive index and absorption coefficient of the semitransparent material are retrieved using the PSAD method as the forward method and using the SPSO algorithm as the inverse method. Finally, the apparent spectral directional emissivities of semitransparent materials can be calculated by the PSAD method according to the retrieval refractive index and absorption coefficient. The innovation of this study is that the measurement system combined with the inverse calculation, reduces the complexity and expands the scope of the measurement system, and allows the measurements of the emissivity for arbitrary direction without blind spots in the viewing range. The main technical indicators of the measurement system include a heating temperature range for the sample of 300 K–1773 K, a spectral range of 2.5 μm–25 μm, and a viewing range of 0°–90°. The reliabilities of the apparent normal spectral emissivity and transmissivity measurement data are verified by comparing the experimental results with those in other references. The feasibility of calculating apparent spectral directional emissivity using the PSAD method is verified by comparing the calculation with the vector Monte Carlo method. By numerically simulated experiments, the apparent normal emissivity and transmissivity can be simulated directly using the PSAD method and serve as simulation experiment data for the inverse analysis. The refractive index and absorption coefficient of the medium can be retrieved by the SPSO algorithm according to the simulated experimental data. The results show that the reasonable retrieval results for the absorption coefficient and refractive index can be obtained by this method even with measurement errors, and demonstrate that the inverse model is reasonable and reliable. After completing the verification of the apparent spectral directional emissivity measurement system, the apparent spectral directional emissivity of sapphire at 773 K is measured by this measurement system, the spectral range being 3 μm–12 μm and the viewing range being 0°–90°. The results obtained show that the proposed method has promise in measuring the directional spectral emissivities of semitransparent materials, which paves the way for a new directional spectral emissivity measurement strategy.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 |