† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11164019, 51562032, and 61565013), the Inner Mongolia Natural Science Foundation, China (Grant Nos. 2015MS0109, NJZZ11166, and NJZY12202), and the Science and Technology in Baotou Production-Study-Research Cooperation Projects, China (Grant No. 2014X1014-01).
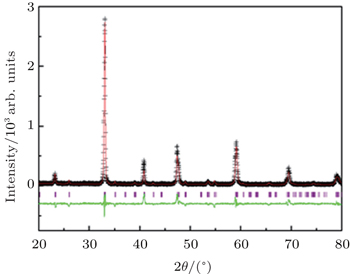
A polycrystalline sample Nd0.5Sr0.3Ca0.2MnO3 is prepared by the conventional solid state reaction method. The structure and magnetic properties are investigated with x-ray diffraction (XRD) patterns, a superconducting quantum interference device (SQUID), and electron spin resonance (ESR). The sample is in single phase with the space group Pbnm symmetry. With the decrease of temperature, Nd0.5Sr0.3Ca0.2MnO3 undergoes three magnetic transitions: ferromagnetic transition at TC ≈ 210 K, charge-ordering at TCO ≈ 175 K, and antiferromagnetic transition at TN = 155 K. In addition, the activation energy Ea ≈ 52.78 meV can be extracted by curve fitting.
Cubic perovskite manganites (R, A)MnO3 (R: rare-earth, such as La, Pr, Nd; A: divalent alkaline-earth, such as Ca, Sr) are a series of Ruddlesden–Popper (RP) compounds. Various physical phenomena are shown in this system due to the coupling of its intrinsic freedom degrees of charge, spin and orbital, such as colossal magnetoresistance (CMR), magnetocaloric effect (MCE), and phase separation (SP), making them an important class of strongly correlated electronic systems.[1–3]
Magnetic transition behavior has been observed in most perovskite manganites, such as La0.65A0.35MnO3 (A = Ca, Sr, Ba),[4] Pr0.6Sr0.4MnO3,[5] etc. Remarkably, paramagnetic insulator, ferromagnetic metallic, and charge ordered–insulator temperature-dependent phase transitions have been induced in the doped manganites. A colossal negative magnetoresistance has been observed near either the concomitant paramagnetic insulator–ferromagnetic metallic phase transition[6] or the ferromagnetic metallic–charge ordered insulator transition.[7] MCE has been discovered in manganite samples around the second order paramagnetic–ferromagnetic transition.[8,9] Zhao et al. studied a ‘colossal’ oxygen isotope shift of the charge-ordering transition in Nd0.5Sr0.5MnO3.[10] This behavior is based on the situation in which Mn3+ and Mn4+ ionic states are implicitly (temporal or spatial) distinguished. The Mn–O–Mn bond length and angle are modified by the Mn3+/Mn4+ distribution, while the charge transfer from an occupied Mn3+ eg orbital to an adjacent Mn4+ unoccupied eg orbital depends strongly on the MnO6 octahedron tilt and Jahn–Teller distortion.
The Ca2+-rich phase can be considered as an electron-doped semiconductor, with significantly reduced resistivity compared with CaMnO3. At fixed x (constant Mn3+/Mn4+ ratio), the replacement of Sr2+ ions by smaller Ca2+ ions causes an anisotropic internal chemical pressure within the compound and leads to a rich variety of magnetically ordered and electrically conductive phases.[11] Electron spin resonance (ESR) is a powerful technique that is sensitive to the various properties of magnetic correlations at a microscopic level, and convenient to clarify the complex magnetic state in doped manganese perovskites. A number of ESR experiments on some manganites have been carried out.[12,13] In the present work, we report the magnetic transition behaviors of Nd0.5Sr0.3Ca0.2MnO3 compound detected by ESR.
The polycrystalline sample of Nd0.5Sr0.3Ca0.2MnO3 was prepared by conventional solid-state reaction processes. At first, the stoichiometric parts of SrCO3, Nd2O3, MnCO3, and CaCO3 were well ground and calcined twice at 800 °C and 1000 °C each for 24 h. Then the resulting powder was pressed into pellets and sintered at 1320 °C for 30 h. The phase purities and crystal structures of the samples were examined by powder x-ray diffraction (XRD) with Cu Kα radiation at room temperature. Data were analyzed with program Retieca. Magnetization measurements were performed in a superconducting quantum interference device (SQUID) magnetometer. The ESR experiments were carried out with a JEOL JESFA200 ESR spectrometer at X-band frequency (f ≈ 9.4 GHz) from 100 K to 300 K.
Figure
Figure
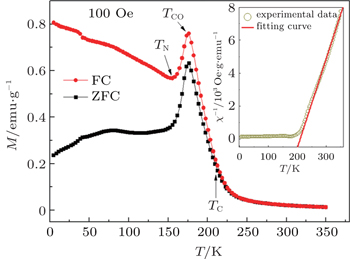 | Fig. 2. Temperature dependences of magnetization measured at 100 Oe, with the inset showing the curve of inverse susceptibility versus temperature. |
Figure
 | Fig. 3. Magnetic field dependences of the magnetization of the Nd0.5Sr0.3Ca0.2MnO3 sample at different temperatures. |
Figure
Figure
In order to obtain more information from the ESR spectra, we analyze the ESR parameters after fitting the spectra. Figures Temperature dependences of the ESR spectrum parameter for the sample, showing temperature-dependent g-value (a), linewidth ΔH (b), and intensity I (c). Insert shows ln(I)–1000/T. The unit 1 Gs = 10−4 T.
We mainly study the structure and magnetic properties of polycrystalline manganite Nd0.5Sr0.3Ca0.2MnO3. The results show that the system is in the paramagnetic state above the Curie temperature (Tc ≈ 210 K). When TCO(≈ 175 K) < T < TC, the system is in ferromagnetic-paramagnetic coexistence and the ferromagnetism, which is caused by the short range ferromagnetic cluster. When 140 K < T < TCO, the system is in antiferromagnetic–ferromagnetic-paramagnetic coexistence. Below 140 K, the system mainly exhibits an antiferromagnetic characteristic. In addition, the activation energy Ea is approximately 52.78 meV at high temperature by fitting, which destroys spin clusters.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 |