The magnetization reversal processes of Fe ultrathin films play an important role in magnetic-storage materials and have attracted sustained interest for both fundamental and technological reasons over the past few decades.^[1–4] The magnetization reversal processes of Fe films occur via coherent rotation and/or domain wall displacement.^[5–7] For Fe (001) single crystalline films, the magnetization reversal processes are primarily dominated by domain wall displacement and can be treated as coherent rotations only at a high external field.^[8–10]

Owing to the high sensitivity down to sub-nm thickness, experimental simplicity and local probing nature, the magneto-optic Kerr effect (MOKE) has been widely employed to investigate the magnetization reversal process.^[11] The MOKE exploits the alteration of the polarization state of light reflected from a magnetic surface, which is exceedingly applicable to the thin films.^[12–14] In the measurements of in-plane magnetization, the Kerr signal depends on the first-order terms of magnetization (M_L and M_T) as well as the second-order terms of the magnetization (M_L M_T, , and ).^[15–18] M_L and M_T are the longitudinal and transverse magnetization components, respectively. In various conditions, a quadratic magneto–optic effect is unavoidable.^[15,19]

A coherent rotation model and a domain wall displacement model have been proposed to account for the magnetization reversal process.^[20] Based on the coherent rotation model, the magnetization will change its orientation to minimize the energy of the system to reach an equilibrium state. While in a coercive field, the magnetization will execute reorientation by nucleation and propagation of new domains to lower the total system energy as indicated by the domain wall displacement model. In the coherent rotation stage, the orientation of the magnetization can be obtained by differentiating the equation of system energy, which is extremely dependent on the magnetic anisotropy constant and the applied field. Yan et al.^[21] have fitted the hysteresis loops including first-order and second-order magneto–optic terms, which shows that the fitting results are in excellent agreement with the experimental results. However, a systematical and accurate method to determine anisotropy constants is still lacking. The rotational magneto–optic Kerr effect (ROTMOKE) is a powerful method to determine the magnetic anisotropy in magnetic thin films by realizing the coherent rotation of magnetization.^[22–24]

In the present paper, the magnetization reversal process in Fe/MgO (001) film is investigated by MOKE. Firstly, the normalized angular-dependent longitudinal and transverse magnetization hysteresis loops are measured with the applied field parallel and perpendicular to the incident plane. The result shows that both coherent rotation and domain wall displacement exist during the magnetization reversal process. Besides, the hysteresis loops exhibit strong asymmetry when the field applied is adjacent to the magnetic hard axis. We further employ ROTMOKE to determine the magnetic anisotropy and simulate the hysteresis loops of the Kerr signal by solving the energy equation and modifying the expression of normalized light intensity including first-order and second-order magneto–optic terms. The obtained results validate the contribution of the quadratic magneto–optic effect to the asymmetry of the hysteresis loops.

Fe/MgO (001) film was grown by molecular beam epitaxial (MBE). The base pressure in the sputtering chamber was better than 3 × 10⁻¹⁰ mbar (1 bar = 10⁵ Pa). The substrate was first annealed at 700 °C for one hour and held at 150 °C during deposition. Fe film was deposited on the MgO (001) substrate at a rate of 0.1 Å/s by an electron-beam gun. The Fe beam was incident along the surface normal of the substrate. The nominal thickness of the sample was 20 nm monitored by a calibrated quartz-crystal oscillator.^[25]

In order to more comprehensively investigate the magnetization behaviors in-plane, it is necessary to measure the two orthogonal magnetization components M_L and M_T. The M_L and M_T are the magnetization components parallel and perpendicular to the applied field, respectively. In this paper, the incident angle of the laser beam on the sample was about 45°. The incident light through the polarizer was S polarized light. The analyzer was set to detect the reflected P-polarized light. In the longitudinal Kerr effect configuration, the hysteresis loops were detected by manipulating the magnetic field parallel or perpendicular to the incident plane.^[26] The relative position between the magnetic field and the sample was fixed, which permits a direct comparison between the longitudinal (M_L) and transverse (M_T) magnetization component loops.

The normalized remanence and coercivity are derived from the hysteresis loops measured by sample rotation with longitudinal Kerr geometry. As respectively shown in Figs. 1(a) and 1(b), the angular dependences of normalized remanence M_r/M_s and coercivity H_C on field orientation clearly verify the in-plane four-fold symmetry for Fe/MgO (001) thin film. However, the measured values of both normalized remanence and coercivity appear to be conspicuously different at the equivalent position from the hard axis. The origin of this abnormal phenomenon is that for the hysteresis loops measured around the hard axis their two branches corresponding to the magnetization reversal processes are asymmetric. Figure 1(c) shows the hysteresis loop measured at φ_H = 31°, where φ_H is the angle between the applied positive field and the Fe [001] axis. Since the value of the normalized remanence is larger than 1 when we use the value of the Kerr signal at the saturation field as a maximum and a minimum for normalization separately, we ascribe the asymmetry in hysteresis loops to the consequence of the quadratic magneto–optic effect on the shape of hysteresis loop,^[18] which is obvious on the Kerr signal at the low field when the value of the transversal magnetization component is large and has no effect on the magnetization reversal process.^[17,18] In the following, we will discuss how to clarify the consequence of the quadratic magneto–optic effect from the measured Kerr signal and show the detailed method. However, we first give the calculated hysteresis loop at φ_H = 31° as shown in Fig. 1(d), in which the normalized value is determined by the linear magneto–optic effect. As clearly shown, the asymmetry in the hysteresis loop, caused by the contribution of the quadratic magneto–optic effect will greatly change the value of the normalized remanence and coercivity. By using the same method, we modify the polar plot for the angular dependences of normalized remanence M_r/M_s and coercivity H_C on the field orientation without the contribution of the quadratic magneto–optic effect as given in Figs. 1(e) and 1(f). The result indicates that both the normalized remanence M_r/M_s and coercivity H_C decrease as the magnetic field rotates to the hard axis and exhibit minima at the hard axis. Moreover, at the equivalent position from the hard axis the values of the normalized remanence and coercivity are comparable.

Fig. 1.

Figure Option ViewDownloadNew Window

Fig. 1. Measured angular dependences of normalized remanence Mr/Ms (a) and coercivity HC (b) on field orientation. The hysteresis loops with (c) and without (d) the contribution of the quadratic magneto–optic effect at φH = 31°, where φH is the angle between the applied positive field and Fe [001] axis; the modified angular dependences of normalized remanence Mr/Ms (e) and coercivity HC (f) on field orientation. The unit 1 Oe = 79.5775 A·m−1.

Figure 2 shows the longitudinal and transverse Kerr signals depending on the applied field. The hysteresis loops each include two branches, A–B–C–D–E–F and F–G–H–I–J–A. On account of the magnetocrystalline anisotropy of Fe/MgO (001), the magnetization reversal process takes place via coherent rotation and/or domain wall placement with the magnetic field applied in the Fe (001) plane. Although both coherent rotation and domain wall displacement can be clearly displayed from the longitudinal or the transverse hysteresis loops, integrated investigation of these two orthogonal components helps to determine the direction of the magnetization vector. As shown in Fig. 2(a), at φ_H = 44°, when the applied field strength decreases from a positive saturated state to zero, the magnetization changes via coherent rotation from the direction of the applied field to the nearest Fe [100] direction, which corresponds to the A₁–B₁ period. Increasing the negative applied field strength to the first switching field (about −26 Oe, 1 Oe = 79.5775 A·m⁻¹), 90° domains with magnetization orientation close to [0-10] are nucleated and unpinned at the edge of the sample, followed by a speedy 90° domain wall displacement.^[21] corresponding to the B₁–C₁ period. At the section C₁–D₁, the magnetization proceeds via coherent rotation towards Fe [0-10]. When the negative magnetic field strength increases up to the second switching field (about −210 Oe), the magnetization rotates closely to [-100] by the second 90° domain wall displacement at the D₁ − E₁ section. Further increasing the negative applied field strength, the magnetization rotates towards the direction of the applied field by a coherent rotation before saturation (E₁–F₁ stage). In the F₁–G₁–H₁–I₁–J₁–A₁, the change of the magnetization is similar to the A₁–B₁–C₁–D₁–E₁–F₁.^[21] The magnetization proceeds with coherent rotation at the stages of F₁–G₁, H₁–I₁, and J₁–A₁, and 90° domain wall displacement takes place at the stages of G₁–H₁ and I₁–J₁.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Hysteresis loops measured from the longitudinal Kerr signal (hollow circle) and transverse Kerr signal (hollow square). The hysteresis loops are corresponding to φH = 44° (a) and 46° (b), φH being the angle between the applied positive field orientation and Fe [100] axis. The azimuth angle is illustrated in the inset.

The hysteresis loop in Fig. 2(b) shows that the magnetization reversal process of φ_H = 46° also occurs by coherent rotation and 90° domain wall displacement. However, the magnetization behaviors are different between at φ_H = 44° and at φ_H = 46°. As clearly shown in Figs. 2(c) and 2(d), when the field is reduced from the positive maximum value to zero, the magnetization of φ_H = 44° proceeds via coherent rotation towards [100] while the magnetization of φ_H = 46° proceeds via coherent rotation towards [0-10]. This result is compatible with the four-fold magnetocrystalline anisotropy of Fe (001).

In order to verify the above description about the magnetization reversal process and clarify the origin of the asymmetry of the hysteresis loops, a quantitative analysis of the magnetization reversal process is performed by simulating the longitudinal Kerr signal.

Generally, four-fold magnetocrystalline anisotropy is accompanied with a weak uniaxial magnetic anisotropy in the Fe (001) plane. We decompose the energy of uniaxial anisotropy to Fe [100] and Fe [110].^[6] The total energy density of the system at the applied field H is given by

Here, ROTMOKE is employed to determine the anisotropy constants.^[27] In order to ensure a coherent rotation process, the applied field should be at least larger than the maximum coercive field in the plane. Figures 3(a) and 3(b) show the direction of the magnetization varying with the direction of the applied field and the angular dependence of the torque curve at different strengths of field. At H = 400 Oe, the direction of the magnetization shows four sudden jumps so that the torque curve is broken down into four intervals because of the four occurrences of 90° domain wall displacement process. Further increasing the applied field to 1000 Oe, the domain wall displacement seems to disappear, and the direction of the magnetization changes with the direction of the field as a result of the coherent rotation process. The magnetic anisotropy constants can be obtained by fitting Eq. (2) to the torque curve under an applied field of 1000 Oe. Using the bulk value of 1.76 × 10⁶ A/m as the saturation magnetization of Fe, the obtained results are K_u1 = 1.6 × 10³ J/m³, K_u2 = 7.5 × 10³ J/m³, and K₁ = 5.6 × 10⁴ J/m³.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. (a) Variations of magnetization direction with applied field and (b) variations of normalized torque l(φM) with φM at fields of 400 Oe, 600 Oe, and 1000 Oe, respectively.

For fitting the experimental data of the longitudinal Kerr signal, we consider both the linear and the quadratic magneto–optic effect. The formula of the detected normalized light intensity, which is obtained based on the proportional relationship between the output current and the squared modulus of the electric field parallel to the analyzer transmission axis, is as follows:^[28]

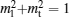
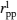
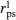
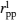
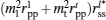
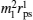
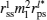
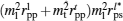
According to the geometrical relationship, M_l = M_s cosθ and M_t = M_s sin θ are obtained, where θ = φ_H − φ_M is the angle of the positive direction of the applied field with respect to the magnetization vector. Therefore, the expression of normalized detectable light intensity in the longitudinal configuration can be rewritten as

According to the minimum energy principle, the orientation of the magnetization φ_M is always changing with applied field H. The calculated anisotropy constants (K_u1, K_u2, K₁) are substituted into Eq. (1) with different H values for given φ_H so as to obtain the value of θ. Then, we substitute θ into Eq. (4) to calculate the value of normalized light intensity and consequently obtain the hysteresis loops with changing magnetic field. The valves of α = 0.9, β = − 0.06822, γ = − 0.2847 show the best fitting of the simulation to the experimental MOKE hysteresis loops for detecting the longitudinal magnetization component.

As illustrated in Fig. 4, the coherent rotation of the magnetization is interrupted by the domain wall displacement at the coercive field. The type of domain wall displacement depends on the direction of the magnetic field. When rotating the field at φ_H = − 1°, the magnetization reversal process takes place via the “l-jump” process (180° domain wall displacement). At φ_H = 44° and φ_H = 46°, the magnetization reversal processes occur via the “2-jump” process (90° domain wall displacement). Besides, the branches of hysteresis loops at φ_H = 44° and φ_H = 46° appear to be asymmetric apparently due to the transverse magnetization component contribution to the light intensity that is used for detecting the longitudinal magnetization component. Since the value of α is much larger than those of β and γ, the contribution mainly comes from the quadratic magneto–optic term M_l M_t. When the field is applied closely to the hard axis, the magnetization aligns parallelly to the direction of the applied field at the saturation field. The transverse magnetization component M_t (sin θ) is almost equal to zero. As the field decreases towards the first switching field, the magnetization presents the coherent rotation to the perpendicular direction of the field after a 90° domain wall displacement process. In the coherent rotation process, M_l M_t will acquire a maximum value so that asymmetry originating from the conspicuous quadratic magneto–optic effect can be observed in the hysteresis loop. However, when the field is applied closely to the magnetic easy axis, the magnetization reversal process is governed by the 180° domain wall displacement. In the whole magnetization reversal process, the contribution of M_l M_t is small and symmetric hysteresis loops are observed.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Simulated hysteresis loops at φH = − 1° (a), 44° (b), and 46° (c), with the simulating parameters being Ms = 1.76 × 103 Gs (1 Gs = 10−4 T), H = 1000 Oe, Ku1 = 1.6 × 103 J/m3, Ku2 = 7.5 × 103 J/m3, K1 = 5.6 × 104 J/m3, α = 0.9, β = − 0.06822, γ = − 0.2847. α, β, and γ are the coefficients of the magneto–optic terms.

The magnetization reversal process of single crystal Fe/MgO (001) thin film is investigated by MOKE. The results show that when the magnetic field is applied along different directions of Fe (001) film, coherent rotation can be interrupted by 90° or 180° domain wall displacement. Based on the longitudinal and transverse hysteresis loops, the magnetization orientation of the Fe (100) plane can be confirmed. Besides, we reveal that the quadratic magneto–optic effect, which comes mainly from the term of M_L M_T, is not negligible in the Fe/MgO (001) thin film. Therefore, it needs to be identified in analyzing Kerr signal data.