The uranium compounds of the UX₃ series (X: a group-IIIA or IVA element in the periodic table) present various interesting magnetic behaviors from an enhanced, Pauli-like paramagnetism (UAl₃, USi₃, and UGe₃), through local spin fluctuations (USn₃), to a local-moment ordering (UPb₃). A great variety of magnetic properties in the UX₃ series are commonly attributed to a hybridization effect between the 5f-electron states of uranium and the s, p, d electronic states of neighboring atoms. The antiferromagnetic compound UGa₃ (T_N = 67 K),^[1–3] crystallizing in the AuCu₃ structure, locates a special position at the onset of magnetic order among the UX₃ phase. The substitution of the group-IIIA (or group-IVA) element for Ga atoms in UGa₃ exhibits interesting magnetic properties through the changes of the hybridization between the uranium 5f electronic states and the conduction electronic states of gallium. For example, with increasing Sn concentration, the f electrons in the UGa_3−xSn_x system undergo a transition from the itinerant antiferromagnetic state to a typical spin fluctuation state, and finally localize for x ∼ 1.^[4] While in UGa_3−xGe_x, the substitution of Ge atoms gradually suppresses the long range magnetic order, and reaches the quantum critical point at x ∼ 0.6, which presents non-Fermi liquid behavior.^[5]

Similarly, the hybridization effect would be changed by the substitution of UGa₃ in the transition metal for Ga atoms since it not only changes the order degree of the occupied atom, but also prominently changes the exchange interactions through changes of environment (the valence electrons and the U–U distance). This concept motivated us to investigate the properties of Mn-doped UGa₃, which present the spin-cluster glass (SCG) state at a low temperature. This compound plays an important role in better understanding the f-electron contributions to the magnetism in uranium compounds.

Single crystals of U(Ga_0.95Mn_0.05)₃ were grown by the Ga self-flux method.^[6,7] The raw materials of U (99.8%), Mn (99.999%), and Ga (99.9999%) were mixed together according to the ratio of U:Mn:Ga = 1:(0.5∼2):10. The feed, placed in an alumina crucible and sealed in an evacuated quartz tube, was heated in a resistance furnace up to 1200 °C, held at this temperature for 24 h and then slowly cooled down to 600 °C at a rate of 1 K/h. Then, the single crystals were separated from the flux by means of centrifuging at 600 °C. The obtained crystals were a cube shape with a maximum dimension of 2 mm× 2 mm× 3 mm.

The actual compositions of the obtained crystals were determined by utilizing energy dispersive x-ray (EDX) microanalysis. All the single crystals prepared by different ratios present the same atomic ratio of U:Ga:Mn, which is 1:2.85:0.15. X-ray diffraction (XRD) was performed on the single crystals and their crushed powder by a diffractometer in a range from 10° to 90°. The frequency-dependent ac susceptibility and low-field magnetization were measured by using a quantum design physical properties measurement system (PPMS). Specific heat experiments were performed in a temperature range of 2 K–200 K on the PPMS using the relaxation method.

Figure 1(a) shows the powder and single crystal XRD patterns for both U(Ga_0.95Mn_0.05)₃ and UGa₃ samples, which can be indexed on the basis of AuCu₃ type structure (Fig. 1(b)). All the powder diffraction peaks of U(Ga_0.95Mn_0.05)₃ shift to a high angle compared with UGa₃ due to the small ionic radius of Mn³⁺. The calculated lattice parameters of U(Ga_0.95Mn_0.05)₃ and UGa₃ are 4.2354 Å and 4.2560 Å, respectively.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. (a) Room temperature XRD patterns of the powder of UGa3 and U(Ga0.95Mn0.05)3 single crystals after grinding. The inset shows the XRD pattern of the corresponding single crystal, showing mainly the c-axis orientation featured with very sharp peaks. (b) Schematic diagram of UGa3 unit cell.

The values of the dc susceptibility χ (χ = M/H) of U(Ga_0.95Mn_0.05)₃ measured in the zero-field-cooled (ZFC) and field-cooled (FC) modes under various applied magnetic fields are shown in Fig. 2. At low fields (e.g., 100 Oe, 1 Oe = 79.5775 A·m⁻¹), the magnetic susceptibility exhibits a sharp increase below 60 K, and an irreversibility behavior is manifested by the bifurcation between the χ_ZFC(T) and χ_FC(T) curves below 41.7 K. Those phenomena, together with results of ac susceptibility, suggest the formation of the SCG state in the U(Ga_0.95Mn_0.05)₃ sample below T_ir. By increasing the magnetic fields, the cusp in the χ_ZFC(T) curve at T_a loses its intensity and broadens, and both T_a and T_ir shift to a lower temperature. These phenomena are typical of spin glass behaviors. In canonical spin glass (SG) systems, the cusp in χ_ZFC(T) is governed by SG dynamic transition and the magnetic irreversibility generally starts at the temperature slightly lower than T_a.^[8,9] The obvious difference between T_ir and T_a in U(Ga_0.95Mn_0.05)₃ suggests the existence of short-range interactional clusters with different sizes. When the system is cooled down from the high temperature in a zero or nonzero field, magnetic moments of the different size spin clusters in U(Ga_0.95Mn_0.05)₃ may be frozen in the directions energetically favored by the strong Ruderman–Kittel–Kasuya–Yosida (RKKY) action or by the external field. There would be a competition between the RKKY action and the external field acting on the spin moment. The RKKY action is predominant at T < T_a and the external field is predominant at T > T_a. Thus, the broad cusp at T_a marks a crossover region where the RKKY action energy and the energy caused by the external field are comparable to each other.

Fig. 2.

Figure Option ViewDownloadNew Window

Fig. 2. DC susceptibility χ (χ = M/H) data for U(Ga0.95Mn0.05)3 measured in the FC (closed symbols) mode and the ZFC (open symbols) mode in various magnetic fields. Ta is denoted by the temperature where χZFC(T) reaches a maximum and Tir is the temperature where χFC(T) and χZFC(T) start to separate from each other. Tm is defined as the temperature where the susceptibility sharply increases. The inset displays the temperature dependence of the inverse molar magnetic susceptibility.

Above 60 K, the reciprocal susceptibility curve can be well fitted by the Curie–Weiss law χ = C/(T − θ_p) (inset of Fig. 2), where C is the Curie constant and θ_p is the paramagnetic Curie temperature. From this fit, the effective magnetic moment and the paramagnetic Curie temperature are determined to be μ_eff = 1.54μ_B/U, and θ_p = 43.7 K, respectively. The obtained μ_eff value is much smaller than that of a free U ion with f² (μ_eff ∼ 3.58μ_B/U) or f³ (μ_eff ∼ 3.62μ_B/U) electronic configuration, suggesting the itinerant behavior of 5f electrons and/or Kondo effect in this compound. The positive sign of θ_p suggests that the ferromagnetic exchange interaction is dominant.

Figure 3(a) shows the dc isothermal magnetizations for U(Ga_0.95Mn_0.05)₃ at various temperatures. The dependence of magnetization on the applied magnetic field at 80 K presents a characteristic linear behavior of the paramagnetic state. However, the magnetization below 60 K exhibits a sharp jump at very low field (H < 500 Oe) followed by a monotonic increase in the high field range without reaching saturation up to 9 T, which provides strong evidence of the existence of the SCG state. By increasing the applied field, the frozen net moment part tends to be saturated, whereas the cluster glass part increases linearly and results in the unsaturation of magnetization. In addition, the small magnetic hysteresis loop (S-type curve) below 60 K shown in Fig. 3(b) also indicates the existence of a frozen net moment in the U(Ga_0.95Mn_0.05)₃ sample.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. (a) Magnetizations up to 9 T and (b) the hysteresis curves measured at various temperatures for U(Ga0.95Mn0.05)3 single crystal.

Figure 4 displays the in-phase and the out-of-phase components of the ac susceptibility for U(Ga_0.95Mn_0.05)₃ at various frequencies f = ω/2π. Both and curves exhibit the characteristic pronounced maxima whose amplitudes and positions strongly depend on the applied magnetic field frequency. These features further confirm an SG state in U(Ga_0.95Mn_0.05)₃ below T_f. Here, T_f is defined as the temperature corresponding to the peak position in the curve. The frequency shift rate δT_f = ΔT_f/(T_fΔ lg ω) = 0.019 for U(Ga_0.95Mn_0.05)₃ falls in a range between canonical spin glasses (e.g., δT_f ∼ 0.005 for CuMn alloy)^[10] and non-interacting ideal superparamagnetic systems (δT_f ∼ 0.1).^[11] This value is comparable to those of a nonmagnetic atom-disorder SG system, such as U₂PdSi₃ (δT_f = 0.020),^[12,13] URh₂Ge₂ (δT_f = 0.025),^[14] and U₂AuGa₃ (δT_f = 0.01).^[15]

Fig. 4.

	Figure Option ViewDownloadNew Window
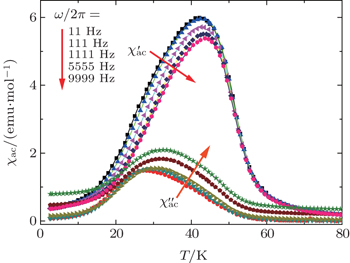	Fig. 4. In-phase and out-of-phase components of the ac susceptibility versus temperature in an applied ac field of 10 Oe at various frequencies for U(Ga0.95Mn0.05)3.

The dynamical parameter, relaxation time τ, follows the conventional power-law divergence of critical slowing down,^[8,9]

The ln–ln plot of relaxation time τ versus [(T_f − T_SG)/T_SG] is shown in Fig. 5(a). The solid line in Fig. 5(a) represents the best fitting result of Eq. (2). The slope and intercept of the plot yield zν = 4.6(2) and τ₀ = 1.5× 10⁻¹⁰ s. Many experimental results give the typical value of zν between 4 and 12 for various spin glass systems,^[16] while zν is usually around 2 for conventional phase transitions.^[9] Moreover, the value of τ₀ is much larger than that of canonical spin glass (10⁻¹³ s),^[9,16] which means a slow spin flip process in U(Ga_0.95Mn_0.05)₃ caused by the strongly interacting clusters rather than individual spins. Hence, T_f ≈ 41.7 K (the maximum in at 11 Hz) can be defined as a cluster spin freezing temperature below which the clusters will be randomly frozen.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. (a) Relaxation time of freezing temperature plotted as ln(τ) versus ln [Tf − TSG]/TSG]. The solid line represents the fit to the power-law divergence. (b) The frequency dependence of freezing temperature plotted as Tf versus 100/ln(ω0/ω). The solid line represents the fit to Vogel–Fulcher law.

The frequency dependence of freezing temperature T_f can be obtained using the empirical Vogel–Fulcher law:^[16–20]

A plot of T_f versus 100/[ln(ω₀/ω)] is shown in Fig. 5(b). The solid line in Fig. 5(b) represents the fit to Eq. (4). Here, we have used the value of attempt frequency ω₀ = 1/τ₀. The determination of characteristic time constant τ₀ = 1.5× 10⁻¹⁰ s, has been discussed before. The slope and intercept of the plot yield T₀ = 380 K and E_a/k_B ≈ 68.5 K (E_a ≈ 1.7 k_BT_f) for our U(Ga_0.95Mn_0.05)₃ sample. The nonzero value of T, arising from the interaction between spins, suggests a cluster spin-glass behavior in the U(Ga_0.95Mn_0.05)₃ compounds. Furthermore, the result that T₀ is very close to T_f suggests that the RKKY interaction is relatively strong in the compound. According to the Tholence criterion, δT_Th = (T_f − T)/T_f, we obtain δT_Th = 0.088 for U(Ga_0.95Mn_0.05)₃, which is comparable to that of the RKKY spin-glass system (e.g., δT_Th = 0.07 for CuMn system).^[19] Therefore, these phenomena indicate that U(Ga_0.95Mn_0.05)₃ has an RKKY spinglass behavior, similar to PrRhSn₃.^[21]

Figure 6 shows the temperature dependences of the specific heat for U(Ga_0.95Mn_0.05)₃ and UGa₃ below 200 K. A λ -type anomaly for UGa₃ is found to be at 67 K corresponding to the antiferromagnetic transition. However, no anomaly was observed in specific heat of U(Ga_0.95Mn_0.05)₃ around T_f. This indicates that no long-range magnetic order exists in this SCG system. The specific-heats of U(Ga_0.95Mn_0.05)₃ and UGa₃ in a temperature range of 2 K–10 K follow the C_p(T) = γT + βT ³ as shown in the plot of C_p/T versus T² (see the inset of Fig. 6). By fitting the experimental data, the electron specific heat coefficient γ of U(Ga_0.95Mn_0.05)₃ is obtained to be 90 mJ/mol·K⁻², which indicates that its electron effective mass is much larger than that of UGa₃. The enhancement of electron effective mass for U(Ga_0.95Mn_0.05)₃ is caused by the spin-cluster glass state resulting from the presence of atomic disorder, as for other nonmagnetic atom-disorder spin glass compounds Ce₂CuGe₃^[22] and Ce₂CuSi₃.^[23]

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Temperature dependences of the specific heat C(T) for U(Ga0.95Mn0.05)3 and UGa3. Inset shows C/T versus T2 plot.

It is generally accepted that both randomness and frustration of magnetic moments are essential to produce the spin glass state.^[9] As for U(Ga_0.95Mn_0.05)₃, the magnetic U atoms form a fully periodic lattice, the 3d half-filled Mn atom and non-magnetic Ga atom randomly occupy the ligand site. The disorders of Mn and Ga atoms in the lattice can destroy the long-range magnetic correlation between U atoms and introduce individual spins or spin clusters with net magnetic moments by the local RKKY interaction. In addition, the Mn atom may have a local magnetic moment which has not been completely screened by the conduction electrons in this compound. Within one layer, U atoms and Mn atoms may form triangles of the nearest neighbors and no single configuration of the spins is extraordinarily favored. Therefore, the combination of the site randomness of Ga/Mn ions and frustration of magnetic moments resulting from the competing ferromagnetic and antiferromagnetic interactions between U ions easily leads to the randomly distributed spin-clusters in U(Ga_0.95Mn_0.05)₃.

The ac and dc magnetic susceptibilities, isothermal magnetization, and specific-heat data of U(Ga_0.95Mn_0.05)₃ single crystal provide conclusive evidence of SCG behavior below the characteristic freezing temperature T_f = 41.7 K. Irreversible magnetism behaviors in ZFC and FC, and a frequency-dependent anomaly in the ac susceptibility reveal a spin-glass behavior with a freezing temperature T_f. The sharp increase in dc susceptibility, a small jump at the very small field in the isothermal magnetization below T_m and no anomaly in the specific heat support the presence of clusters with frozen moments. We deem that the disorders of Mn and Ga atoms in the crystal lattice and frustration of magnetic moments lead to the random distribution of spin-clusters below T_f.