The discovery of unconventional superconductivity in iron pnictides^[1] has aroused a tremendous amount of research into this class of materials in an effort to understand the mechanism of high-T_c superconductivity, as well as to explore materials with higher T_c. The parent compounds of these iron-based superconductors (FeSCs) are poor Pauli-paramagnetic metals in their high-temperature phase, and undergo structural and antiferromagnetic (AFM) phase transitions upon cooling down to low temperature.^[2–4] Superconductivity emerges with the suppression of the AFM order via chemical substitution^[5–7] or the application of pressure.^[8–11] Since optimal superconductivity is accompanied by the disappearance of the AFM phase, AFM spin fluctuations have been proposed to mediate the electronic pairing in FeSCs.^[12] On the other hand, previous spectroscopic studies have also revealed strong competition between the AFM order and superconductivity in the Ba122 system.^[13,14] Therefore, the relation between magnetism and superconductivity is still a matter of debate in FeSCs.

In this article, we report our results of magnetotransport measurements on BaFe_2−xNi_xAs₂ single crystals with different Ni concentration. An abrupt drop of the resistivity at ∼22 K in underdoped x = 0.03 has been observed in the temperature-dependent resistivity as evidence for the onset of filamentary superconductivity (FLSC). An external magnetic field suppresses FLSC in a manner similar to the suppression of the bulk T_c in an optimally-doped (x = 0.10) sample, suggesting a possible connection between FLSC and bulk SC. In addition, FLSC is robust and exhibits little doping dependence in the underdoped regime, but vanishes abruptly in the overdoped region where long-range AFM order is absent. These results indicate that the emergence of FLSC is intimately related to the magnetic order in FeSCs.

High-quality single crystals of BaFe_2−xNi_xAs₂ with a series of Ni doping were grown using a self-flux method.^[15] Typical dimensions of single crystals for measurements are approximately 1 mm × 0.25 mm × 0.05 mm. In-plane resistivity was measured as a function of temperature in a physical property measurements system (PPMS-9, Quantum Design) using a standard four-electrode method. The current used for measurements is parallel to the basel plane and I = 1 mA.

Figure 1 shows the temperature dependence of normalized resistivity ρ(T)/ρ(300 K) for x = 0.03 underdoped and x = 0.10 optimally doped BaFe_2−xNi_xAs₂ samples. For x = 0.10, the curve is characterized by a steep superconducting transition at T_c = 20.3 K. The x = 0.03 sample features a metallic behavior followed by an upturn resistivity at the spin-density-wave (SDW) transition temperature T_N = 109 K, corresponding to a sharp dip in the derivative of the resistivity dρ/dT as a function of temperature. Meanwhile, as shown in the upper inset in Fig. 1, an abrupt drop of resistivity can be clearly identified at low temperature T_fl ≈ 22 K for the x = 0.03 sample. Our recent studies on CaFe₂As₂^[16] and BaFe_2−xCo_xAs₂^[17] has demonstrated that this step in the resistivity is due to the presence of weakly pinned superconducting filaments. Furthermore, we have also provided evidence that filamentary superconductivity nucleated at antiphase domain walls in antiferromagnetic CaFe₂As₂. Therefore, we define the temperature of this step in resistivity as the onset of FLSC (T_fl), similar to the high-T_c cuprates^[18,19] and heavy fermions superconductors.^[20,21]

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. The temperature-dependent normalized resistivity ρ(T)/ρ(300 K) curves for BaFe2−xNixAs2 single crystals with x = 0.03 and x = 0.10. Top inset: the enlarged view of ρ(T)/ρ(300 K) curve for underdoped x = 0.03 sample; Bottom inset: the derivative curve dρ/dT for x = 0.03 sample.

The top panel of Fig. 2 shows ρ(T) curves from 2 K to 110 K at different magnetic fields for underdoped BaFe_2−xNi_xAs₂ (x = 0.03). While no magnetoresistance is observed above the magnetic transition temperature T_N, a peak feature related to FLSC is observed at temperature T_fl in all curves. It is noticed that T_fl decreases with increasing magnetic fields. The H–T phase diagram obtained from the field dependence of T_fl for the x = 0.03 sample and the field dependence of bulk T_c for the x = 0.10 sample are shown in the bottom panel of Fig. 2. A striking similarity of the suppression by external magnetic field between T_fl and T_c is found through the comparison of these H–T phase diagrams, which suggests a close connection between FLSC and bulk SC and rules out the possible contribution of an impurity phase to this phenomena.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. (a) Temperature-dependent reduced resistivity ρ(T)/ρ(300 K) curves for BaFe1.97Ni0.03As2 single crystal with different applied magnetic fields (H = 1 T–9 T). (b) H–T phase diagrams of BaFe2−xNixAs2 single crystal (x = 0.03 and x = 0.10). The black solid lines are fits of the data by using the GL expression, the red dotted lines are fits with the Werthemer–Helfand–Hohenberg (WHH) model.

In addition, the upper critical fields in these two samples are also fitted by the Ginzburg–Landau (GL) model and the Werthamer–Helfand–Hohenberg (WHH) model. As shown in the bottom panel of Fig. 2, the solid curve is a fit with GL expression,

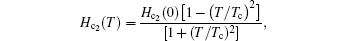
While we observed an obvious drop of resistivity in ρ(T) curves for the x = 0.03 sample, some studies showed that the step in the low-temperature resistivity is not always observed in 122-type parent compound in iron pnictide superconductors. For example, Xiao et al. reported that this step was observed only for small and thin single crystals in undoped BaFe₂As₂.^[17] Tanatar et al. studied different samples of parent compounds CaFe₂As₂ and BaFe₂As₂, and found that two samples showed the partial superconducting transition in three undoped CaFe₂As₂, and even only two samples showed the partial superconducting transition in five different BaFe₂As₂ samples.^[24] For this reason, we performed magnetoresistivity measurements, which is believed to be more sensitive to the small decrease in resistivity due to filamentary superconductivity.

Figure 3 shows the temperature dependence of magnetoresistivity Δρ/ρ(0) = [ρ(9 T) − ρ(0 T)]/ρ(0 T) for different Ni concentrations. As the temperature decreases, the magnetoresistivity Δρ/ρ(0) for the underdoped x = 0.03 sample increases very gently at first, but then an abrupt increase occurs close to 22 K, which is exactly the FLSC onset temperature T_fl in the zero-field ρ(T) curve. Therefore, we attribute this abrupt change in magnetoresistivity to the occurrence of filamentary superconductivity and identify the temperature as T_fl. We also performed magnetoresistivity measurements on several other pieces of crystal of underdoped x = 0.03 samples and confirmed that the abrupt change in magnetoresistivity always exists at a temperature T_fl even in some samples where the step in ρ(T) curve has not been detected. Furthermore, the abrupt change in magnetoresistivity is observed in other Ni-doping BaFe_2−xNi_xAs₂ single crystals in Fig. 3.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. (a) Temperature-dependent magnetoresistivity [ρ(9 T) − ρ(0 T)]/ρ(0 T) curves for BaFe2−xNixAs2 single crystals with x = 0.03, 0.05, 0.065, 0.085, 0.092, and 0.096. Data were offset vertically to separate the overlapped curves between different doping.

In Fig. 4, we make a comprehensive plot of the phase diagram of the doping dependence of structural transition temperature T_s, magnetic transition temperature T_N, superconducting transition temperature T_c, and FLSC transition temperature T_fl. The defination of T_s, T_N, and T_c is shown in Fig. 1. From the phase diagram we find that the parent compound BaFe₂As₂ exhibits simultaneous structural and magnetic phase transitions at ∼140 K, from high-temperature tetragonal paramagnetic to low-temperature orthorhombic antiferromagnetic phase. With increasing Ni doping, the structural and magnetic transitions separate from each other with T_N slightly lower than T_s. The antiferromagnetic order is suppressed by replacing Fe by Ni in BaFe₂As₂. Superconductivity emerges at x ≈ 0.05 and reaches a maximum at x = 0.10 where long-range AFM order vanishes. Most importantly, we find that T_fl is less doping dependent compared with the bulk superconductivity T_c and it exists in underdoped samples and persists up to the edge of the optimally-doped x = 0.10 sample, where the AFM order vanishes. This suggests a close relationship between FLSC and AFM order.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Doping-x dependence of Ts, TN, Tc, and Tfl phase diagram. Tfl in parent compound BaFe2As2 is obtained from Ref. [17].

However, some recent experimental results revealed that SC and AFM order parameters are spatially modulated on a microscopic scale in iron pnictides.^[24–26] For example, many studies showed the evidence for the existence of the structural domain like twin boundary and antiphase domain wall in the iron pictides.^[24,26] Meanwhile, a recent SQUID microscopy study in underdoped Ba(Fe_1−xCo_x)₂As₂ showed an enhanced superfluid density on twin boundaries^[25] and ⁷⁵As nuclear magnetic resonance (NMR) measurements in antiferromagnetic CaFe₂As₂ suggests the presence of FLSC nucleated at the AFM domain walls.^[16] All these results indicate that AFM order is vital to the emergence of SC in iron pnictides.

In combination with our previous studies in CaFe₂As₂ and Ba(Fe_1−xCo_x)₂As₂,^[16,17] we find that FLSC exists in electron-doped 122-type iron-based superconductors and it has a close connection with AFM order. Besides, Chu et al. also revealed an obvious FLSC with a high T_c = 49 K in single crystalline CaFe₂As₂ via electron-doping by partial replacement of Ca by rare-earth.^[27,28] Thus our results suggest that the FLSC may be a common feature in the AFM phase of iron pnictides due to strong coupling between AFM and superconductivity, further exploration is needed to verify it.

In conclusion, magnetotransport measurements have been carried out on a series of Ni doping BaFe₂As₂ single crystals. A similar suppression of FLSC T_fl and bulk SC T_c by external magnetic field is depicted in the H–T phase diagram. The doping-temperature phase diagram reveals the following results: (i) FLSC is less doping-dependent compared with bulk SC; (ii) FLSC coexists with AFM order and vanishes in the edge of optimal doping where long-range AFM order is absent. Based on our results, we conclude that FLSC is closely linked with magnetic order and the bulk SC in iron pnictides.