Tunnelling through a nanostructure is an interesting physical phenomenon closely related with the properties of the nanostructure in question. From the first side, it allows one to investigate the characteristics of the nanostructure using the tunnelling as an instrument.^[1] From the other side, it creates an opportunity to construct new nanoelectronic devices based on the tunnelling peculiarities. Electron tunnelling through quantum dots with connected leads is studied, e.g., in Refs. [2], [3], and [4]. Interesting results were obtained for tunneling through periodic arrays of quantum dots.^[5,6] An explicitly solvable mathematical model for a description of tunnelling through a nanodevice was suggested in Refs. [7] and [8]. It is based on the theory of self-adjoint extensions of symmetric operators. The model is rather universal and allows one to describe tunnelling through different structures. Due to nanotechnology progress, it is possible now to create curved two-dimensional nanostructures (e.g., fullerene-like structures and metallic nanospheres). The above mentioned model is appropriate to describe tunnelling through this structure. Namely, tunnelling of a non-relativistic electron through a sphere with attached semi-infinite leads was studied in Ref. [9]. An explicitly solvable model for the analogous problem dealing with the sphere in a magnetic field was constructed and investigated in Ref. [10]. In the present paper we study tunnelling of a relativistic electron through a sphere with attached leads. We consider the Dirac operator on the semi-axis and the sphere and construct a model based on the operator extensions theory.

Through the present paper we consider the sphere S with two attached wires ℝ₊ and ℝ₋. The behavior of a relativistic spinless particle is described by the Dirac operator. It has the following form (see, e.g., Refs. [11] and [12]):

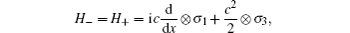
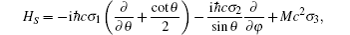
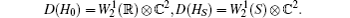
The starting operator for our model is the direct sum of the operators described above

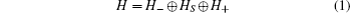
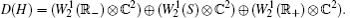
To switch on an interaction between parts of our system, we construct the model operator in the framework of the theory of self-adjoint extensions of symmetric operators. Namely, we use the so-called “restriction-extension” method (see, e.g., Refs. [13], [14], and [15]). We denote the restriction of the operator H_± by D_± and the restriction of H_S by D_S.

The Hamiltonian of the system is constructed as a self-adjoint extension of the operator

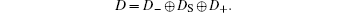
To describe these extensions, we use the Krein formula for resolvents (see, e.g., Refs. [13], [15], and [16]

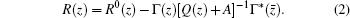
The Green function for the Dirac operator on the half-line is known^[17]

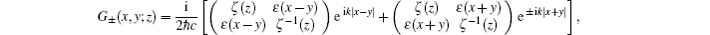
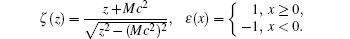
The expression for the Green function of the Dirac operator on the sphere is obtained in Appendix A.

To construct the extensions by formula (2), we choose the matrix A (of size 8×8) in the following form

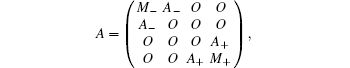
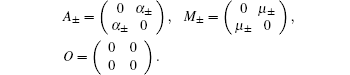
The Krein Q-matrix for the model operator has the form

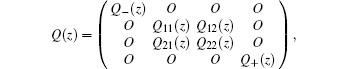
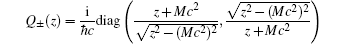
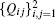
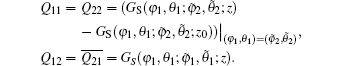
Further, we consider the scattering problem. Let us take the incoming wave in ℝ₋ in the form

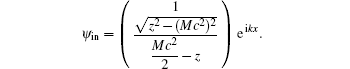
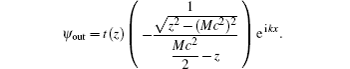
After straightforward algebraic manipulations, one obtains the following formula for the transmission coefficient T(z) = |t(z)|,

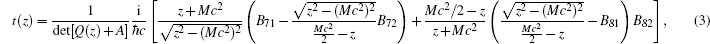
The dependence of the transmission coefficient on energy is shown in Fig. 1. We use atomic units, i.e., we assume c = ħ = 1, M = 1/2, and R = 1. The dependence has a strongly resonant character. The resonances are close to the eigenvalues of the Dirac operator on the sphere. As for details, one observes the resonances of two types (Breit–Wigner resonances and Fano resonances). More precisely, there are pairs including the resonances of these two types. These resonances appear near the eigenvalues (λ_mn, see Appendix A) of the unperturbed Hamiltonian (for the sphere without connected leads). Taking into account the asymptotics of Q_ij near λ_mn, one can describe two types of resonances in more detail. Namely, the Breit–Wigner resonances are related with the poles of the transmission coefficient on the nonphysical sheet of the energy Riemann surface. In the neighborhoods of these poles , the transmission coefficient t(z) can be represented in the following form:

Fig. 1.

	Figure Option ViewDownloadNew Window
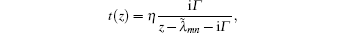
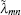
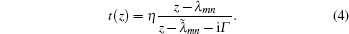
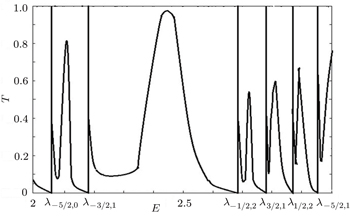	Fig. 1. Dependence of the transmission coefficient on energy; T is dimensionless, E is in atomic units, i.e., we assume c = ħ = 1, M = 1/2. Eigenvalues corresponding to Fano resonances are marked.

Fano resonances are characterized by a closely spaced zero and a peak of the transmission coefficient. They are associated with the interference between the localized states of a discrete spectrum and propagating electron waves. As for the position of the resonance, formula (4) shows that the Fano resonance curve has a zero at the eigenvalues λ_mn of the unperturbed operator. The analogous resonant behavior takes place for tunnelling of non-relativistic electron (i.e., for the Schrödinger operator instead of the Dirac one), see Ref. [9]. Namely, for a non-relativistic electron, one observes pairs of the Breit–Wigner and the Fano resonances too. There is a difference: for the relativistic electron, the Breit–Wigner peaks are sharper than for the non-relativistic one.