The specific characteristics of surface plasmon (SP) in the terahertz (THz) region of concentrating and guiding waves utilizing subwavelength structures arouse the great interest of many researchers. For decades, applications based on SP have been promoted in various regions, such as waveguide, laser antenna and sensor.^[1–5] A beam splitter is an optical device that splits a beam of light into two or more beamlets. In the terahertz region, the design and research of the beam splitter has been conducted for several years. By different methods, a THz beam can be split by different polarizations^[6] or wavelengths.^[2,7] In the present work, we present a design of beam splitter based on SP resonance transition between propagating surface plasmon (PSP) and localized surface plasmon (LSP), which can split a THz beam, with its optical properties unchanged. By utilizing the finite element method (FEM), the transmission properties of the splitter and effects of SP resonances (both PSP and LSP) are studied. Analysis shows that the resonance transition between PSP and LSP plays a key role in the process of beam splitting. The transition can be explained by a coherent electronic cloud displacement model. The design of the splitter has a relatively broad operating frequency region.

The beam splitter is a centrosymmetric cross structure which is composed of four parallel corrugated metal plates (PCMPs) and a pair of metal blocks engraved with an air loop as shown in Fig. 1. The four PCMPs are placed around the pair of metal blocks as couplers and waveguides to trigger the PSP resonance. The geometry parameters of PCMP denoted in Fig. 1(c) are as follows: cell array periodicity d is 100 μm, groove depth h is 100 μm, groove width a is 50 μm, and distance between two plates w is 100 μm. Two metal blocks placed at the center are engraved with air loops. The geometry parameters of metal blocks are as follows: outer radius R is 75 μm, inner radius r is 25 μm, depth h is 100 μm, and distance between two blocks w is 100 μm as shown in Fig. 1(d). To better illustrate the centrosymmetric structure, we choose one port of the PCMP as the input port and the label is referred to as port 1, the other three ports are named port 2, port 3, and port 4 in a counterclockwise direction, as figure 1(b) shows.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. (a) Single layer of the splitter, where a metal block is surrounded by four periodic corrugated metal plates; (b) three-dimensional schematic model of the splitter; (c) schematic model of PCMP and its corresponding parameters; (d) top view of the metal block engraved with air loop and its corresponding parameters.

Surface plasmon (SP) wave (SPW) emerges when an incoming electromagnetic wave excites collective electronic oscillations at the interface of metal/dielectric. According to different properties, the SP can be termed PSP and LSP.^[8] For PSP, the SPW is confined and propagates along the surface of metal. In the terahertz region, periodical structures corrugated on a metal surface are needed for momentum matching. For the LSP, the charge density oscillations are present around metallic subwavelength structures and non-propagating. In contrast with the PSP, the LSP resonance mainly depends on the size and shape of the metallic structure while the PSP mainly depends on lattice constant.^[9,10]

As is well known, the SP resonance is triggered by transverse magnetic (TM) wave,^[11] thus the incident wave is in the TM mode with its wave vector straight along the x axis. The metal was set as a perfect electric conductor (PEC) in simulations since the dielectric constant of metal is very large in the terahertz region which approaches to that of PEC.^[12,13] The energy transmittance spectrum of the splitter is first simulated and plotted in Fig. 2. The energy transmittance equals the output energy (integral time average power outflow) divided by the input energy. Figure 2 contains three transmittance curves which are corresponding to ports 2, 3, and 4, respectively. It is obvious that the output energies of ports 2 and 4 equal each other in the whole frequency range. In the lower frequency range from 0.1 THz to 0.56 THz, the output energy of port 3 is close to those of port 2 and port 4, thus the structure can act as a beam splitter.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Energy transmittance spectra of ports 2 (solid), 3 (dashed) and 4 (dotted).

Figure 2 also reveals a stop-band from 0.56 THz to 0.87 THz and a passband from 0.87 THz to 1.2 THz. To illustrate the transmission properties of the splitter, further studies are carried out on PCMP and the metal block engraved with an air loop.

Figure 3 shows the dispersion curves and transmittance spectra of PCMP. The great influence of PCMP on the splitter is obvious and easy to understand since the THz wave is input and output from it. The passband and stopband of the splitter correspond well to those of the PCMP. In the lower frequency region where the splitter operates, the dispersion line of the PCMP is below the light line (the nonradioactive region) which means that the THz wave is coupled as SP mode (specifically, PSP). In the higher frequency range beyond 0.87 THz, the THz wave is coupled and propagates in the guided mode and the transmittances of three ports are greatly inconsistent. According to the comparison of the transmittance spectrum between PCMP and splitter, the operating frequency range of the splitter is the same as the PSP resonance frequency range of the PCMP. It is naturally deduced that the SP resonance plays a key role in the process of beam splitting.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. (a) Transmittance spectrum of PCMP and its corresponding dispersion curves; (b) transmittance spectra of PCMP at three output ports of the splitter.

The SPW is characterized by E_z, thus the role of SP resonance can be well clarified by electric field distributions of E_z as shown in Fig. 4.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Electric field density distributions (f = 0.4 THz) of Ez on cross structure for (a) x–y plane view on the surface of the metal plate, (b) y–z plane view, and (c) z–x plane view across the center of metal blocks. Electric distributions of cross structure with metal cylinder separated from substrate for (d) y–z plane view and (e) z–x plane view across the center of metal blocks.

Figures 4(a)–4(c) show the E_z distributions of the splitter. Figure 4(a) shows that the electric field is strong in port 1, then converges at the surface of the metal cylinder in the center and splits into three electric fields that enter into ports 2, 3, and 4 respectively. Figures 4(b) and 4(c) show the y–z plane view and z–x plane view of the electric distribution. It can be observed that E_z is confined on the surface of metal, which is the major characteristic of SP. It is also revealed that E_z not only emerges on the surfaces of PCMPs, but also on the surfaces of metal cylinders. That means that the SP resonance is also present on the metal cylinder. To figure out the relationship between SP resonance on the PCMP and the metal cylinder, we simulate the field distribution of the splitter structure with metal cylinders separated from substrates as shown in Figs. 4(d) and 4(e). Since the charge density oscillation of PSP resonance is continuous, the structure in Fig. 4(d) excludes the possibility of PSP mode on metal blocks. In other words, the SP resonance on metal cylinders could be induced only by LSP, the charge density oscillation is around the metal cylinder and non-propagating.

Unlike the PSP, the dispersion relations of LSP were acquired by quasi-static calculation,^[8] which contain two modes characterized as longitudinal and transversal modes. The wave-vector direction of the transversal mode is perpendicular to that of the longitudinal mode. The transversal mode has a wave vector direction perpendicular to the input vector which would propagate to ports 2 and 4. The longitudinal mode wave is in the same vector direction as the input wave, which would propagate to port 3. The resonance of LSP leads to the splitting of the THz beam. The whole transmission process is a resonance transition from PSP to LSP and then back to PSP. To clarify the transition between PSP and LSP, the electric field distributions of E_x and E_y are simulated, and the results are shown in Fig. 5.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Partially magnified electric field distribution of cross structure in the x–y plane: (a) Ex at f = 0.4 THz; (b) Ey at f = 0.4 THz; (c) Ex at f = 0.95 THz; (d) Ey at f = 0.95 THz.

Although the SPW is characterized by E_z, E_x, and E_y could well exhibit the resonance between PSP and LSP. It can be observed from Figs. 5(a) and 5(b) that E_x and E_y cannot be confined on the metal surface and they exist in air, the phases of electric field are opposite on either edge of the air loop, which means that the density charges of the metal cylinder are opposite to those of its outer surrounding metal. For comparison, we also simulate the field distributions of E_y and E_x at f = 0.9 THz where THz wave is coupled as guided mode, which are shown in Figs. 5(c) and 5(d). The field distributions on metal block at f = 0.9 THz show obvious optical properties of reflection and diffraction.

According to the field distributions of E_x and E_y, it can be deduced that the transition between PSP and LSP is due to the charge density oscillation resonance between the cylinder and its outer surrounding metal in the center. Figure 6 shows that resonance transition. The collective electronic oscillation expands to the edge of the PCMP as the SPW propagates. When the negative electric charges converge at the edge of the PCMP, the coherent electron cloud of the metal cylinder is repelled by an electrostatic repulsive force. When the positive electric charges converge at the edge of the PCMP, the coherent electron cloud of the metal cylinder is attracted by electrostatic attraction. In that way, the alternative variation of electric charge on the edge of PCMP leads to the displacement of coherent electron cloud and excites the LSP resonance.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Schematic diagrams of resonance transition between PSP and LSP.

According to the above analyses, it can be deduced that the transmission process of the splitter is as follows: the input THz wave irradiates the PCMP structure and couples as PSP mode, which is confined on the surface of metal plates. When the PSP wave propagates to the outer edge of air loop, the charge density oscillation caused by PSP would induce the charge density oscillation in the metal cylinder and induces the resonance of LSP. The LSP mode contains both longitudinal mode and transversal mode. The longitudinal mode decouples along the direction of the input wave, which is along the x-axis. The transversal mode decouples in the direction perpendicular to the input wave direction which is along the y axis. Then the decoupled waves of both longitudinal and transversal modes couple again as the PSP mode and propagate along the PCMP structure till the output ports. According to the transmittance spectra in Fig. 3(b), the whole transmittance of the cross structure between 0.1 THz and 0.4 THz is 60% (or 75% of PCMP’s transmission energy). The transmittance spectrum of PCMP shows about 20% energy loss which is mainly caused in the process of wave decoupling from PCMP to free space and can be improved by utilizing couplers. Since the wave decoupling from LSP propagates to all the four ports, nearly 20% energy propagates back to port 1.

The influences of geometry parameters on the splitter can be divided into two parts: the parameters of PCMP for PSP resonance and those of the metal block for LSP resonance.

The geometry parameters of PCMP mainly affect the operating frequency range of splitter. The dispersion relation of PSP on PCMP could be calculated by the modal expansion method as^[14]

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. Dispersion curves of PCMP with (a) h = 0.5d, 0.75d, and d; (b) w = 0.5d, d, and 1.5d; (c) a/d = 0.25, 0.5, and 0.75.

It can be observed from Fig. 7(a) that the cut-off frequency of PSP increases as the decreasing of h. On the other side, however, the dispersion curve of PSP mode corresponding to smaller h becomes closer to the light line, which will weaken the confinement of SPW on the metal plate and degrade split performance. A modest value of h is needed to achieve a relatively large operating frequency range and better confinement of SPW. For that reason, we chose h = 100 μm in the design.

For different values of w and a/d, a similar dilemma to h occurs that the larger operating frequency will induce weaker confinement of SPW in the lower-frequency region (actually, according to the dispersion curves in Figs. 7(b) and 7(c), the influence of w and a/d on the operating frequency region is much smaller than that of h). With the same consideration of balance, the values of w and a/d are chosen to be w = d and a/d = 0.5.

The LSP resonance emerges on the surface of the metal cylinder in the center, thus the resonance can be affected by the cylinder radius r. According to Mie theory, the resonance frequency of LSP is related to plasma frequency by

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. Transmittance spectra of cross structure (d = 100 μm, a = 50 μm, h = 100 μm, w = 100 μm, R = 75 μm) with r = 50 μm, 25 μm, and 6.25 μm, respectively.

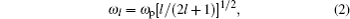
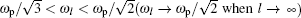
A broad band beam splitter operating in the terahertz region is presented in this work. With the help of FEM, the transmission properties are analyzed. The process of beam split is based on the resonance transition between PSP and LSP. The input THz wave is coupled as a PSP mode in the PCMP structure, then is converted into the LSP mode when irradiating the metal cylinder. The longitudinal and transversal modes of LSP are decoupled along the perpendicular direction and recoupled as the PSP mode again in the PCMP structure. The operating frequency of splitter is in the lower frequency range corresponding to the PSP resonance range of PCMP. From 0.1 THz to 0.4 THz, output energies of three ports are very close to total energy with a transmission efficiency of 60%. Compared with traditional beam splitters which can split light into two beamlets with different polarizations at a certain frequency, the splitter proposed in this paper provides a way to split a THz wave into three wavelets with the optical characteristics(such as phase and polarization) unchanged and has a relatively broad range of operating frequency.