Cite this Article
Abdelkrim Allag, Rahmane Saâd, Abdelouahab Ouahab, Hafida Attouche, Nabila Kouidri. Optoelectronic properties of SnO2 thin films sprayed at different deposition times. Chinese Physics B, 2016, 25(4): 046801  
Permissions
Optoelectronic properties of SnO2 thin films sprayed at different deposition times
Abdelkrim Allag, Rahmane Saâd†, , Abdelouahab Ouahab, Hafida Attouche, Nabila Kouidri
Laboratoire de Physique des Couches Minces et Applications, Université de Biskra, BP 145 RP, 07000 Biskra, Algérie

 

† Corresponding author. E-mail: rahmanesa@yahoo.fr

Abstract
Abstract

This article presents the elaboration of tin oxide (SnO2) thin films on glass substrates by using a home-made spray pyrolysis system. Effects of film thickness on the structural, optical, and electrical film properties are investigated. The films are characterized by several techniques such as x-ray diffraction (XRD), atomic force microscopy (AFM), ultraviolet-visible (UV–Vis) transmission, and four-probe point measurements, and the results suggest that the prepared films are uniform and well adherent to the substrates. X-ray diffraction (XRD) patterns show that SnO2 film is of polycrystal with cassiterite tetragonal crystal structure and a preferential orientation along the (110) plane. The calculated grain sizes are in a range from 32.93 nm to 56.88 nm. Optical transmittance spectra of the films show that their high transparency average transmittances are greater than 65% in the visible region. The optical gaps of SnO2 thin films are found to be in a range of 3.64 eV–3.94 eV. Figures of merit for SnO2 thin films reveal that their maximum value is about 1.15 × 10−4 Ω−1 at λ = 550 nm. Moreover, the measured electrical resistivity at room temperature is on the order of 10−2 Ω·cm.

PACS: 68.55.ag;68.35.bg;81.05.Bx;
Keyword:thin film;SnO2;spray pyrolysis;thickness;properties;
1. Introduction

Transparent conducting oxides have been a research subject for years.[1–4] SnO2 is of interest because it is a naturally non-stoichiometric prototypical transparent conducting oxide. It has a wide band gap of 3.6 eV, plasma frequency in the IR region and when suitably doped, it can be used as both a P-type and N-type semiconductor.[5,6] SnO2 thin film is transparent in the region above 400 nm, which is the region of interest for electrochromic devices. Doping tin oxide with fluorine, chlorine, antimony etc.[7,8] as donor impurities yields films with a low sheet resistance.[9]

SnO2 films were used extensively as transparent electrodes in display devices like liquid crystal displays (LCDs) and as transparent active layers in SnO2 silicon solar cells,[10] thin film resistors, antireflection coatings, photochemical devices and electrically conductive glass.[11] Among the varieties of methods that have been proposed for depositing films of SnO2, spray pyrolysis has been found to be attractive in the sense of its simplicity and low cost.

The aim of this research is to establish a relationship between the film thickness and the film properties. In order to achieve this goal, tin oxide films are prepared by a spraying method at various deposition times ranging from 1 min to 5 min. The properties of the films are characterized by x-ray diffraction analysis (XRD), atomic force microscopy (AFM), ultraviolet-visible (UV–Vis) spectroscopy, and four-point conductivity measurement methods.

2. Experimental procedure
2.1. Solutions and thin film preparation

The tin oxide films were prepared using a home-made spray pyrolysis system. In this deposition technique, liquid precursors were sprayed by atomization processes and condensed by thermal decomposition on substrates maintained at elevated temperatures. The sprayed micro-droplets reaching the hot substrate surface underwent pyrolytic decomposition and formed a single crystallite or a cluster of crystallites of the sprayed materials. Stannous chloride (SnCl2, 2H2O) was used as a precursor for tin. This tin precursor dissolved in distilled water with adding a few drops of hydrochloric acid (HCl). The precursor concentration was fixed to be 0.15 mol/l. All spray solutions were magnetically stirred to obtain homogenous solutions. The resulting solutions were sprayed on glass substrates. The normalized distance of 30 cm between the spray nozzle and the substrates was maintained. The spray solution quantity of 100 ml was kept fixed during the growth. Filtered compressed air was used as the gas carrier. The deposition time was varied from 1 to 5 min. The substrate (working) temperature was maintained at 500 °C by an electronic temperature controller connected to the heater. After deposition, the coated substrates were cooled down naturally to room temperature.

The formation of SnO2 film from a SnCl2 solution gives rise to a transitory formation of the compound SnO. The relevant chemical reactions are[12–14]

SnCl2 can partly be decomposed and ionized into Sn2+ and Cl−; it could also form tin based polymer molecules.[13] On the other hand, it was reported that the presence of HCl in SnCl2 solution leads to the formation of different intermediate molecules in the starting solution. The occurrence of HCl that results in the transparent solution may be due to the breakdown of those tin based polymer molecules. SnCl2·2H2O is known to react with HCl to give HSnCl3. At the pyrolysis temperature, HSnCl3 is thermally decomposed to form the SnO2 molecules.[12,14]

2.2. Characterization

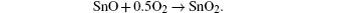
The structural characterization of the SnO2 thin films was carried out by x-ray diffraction (XRD) measurements with using a BRUKER D8 ADVANCE diffractometer with Cu Kα radiation (λ = 1.541838 Å). The diffractometer reflections were measured at room temperature and the values of 2θ were varied between 20° and 80°. The surface morphologies of the films were observed using an A100 Atomic Force Microscope. The dc electrical resistivity was measured in the dark and at room temperature with a four-point probe technique. The film optical transmittance was recorded by using a SHIMADZU 1800 UV-visible scanning spectrophotometer in a spectral region between 200 nm and 800 nm.

3. Results and discussion

Each of the films deposited on glass substrates are physically stable and have a good adherence to the substrate (hardly peeled with the scotch tape test).

3.1. Measurement of thickness

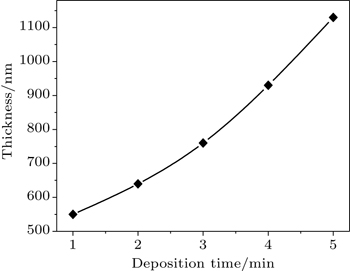
The film thickness (t) of SnO2 thin film is measured by the gravimetric method using the relation

where A is the surface area of the film, M the mass of the film material, and g the density of the film material.

The thickness values of the films are found to be between 550 nm and 113 nm as listed in Table 1. Figure 1 shows the plot of film thickness versus deposition time, and it is clear that the film thickness increases continuously with increasing deposition time due to the relative increase in the amount of tin sprayed. The values of growth velocity (Gv) of thin films are estimated from this plot to be 145 nm/min.

Table 1.

Values of lattice parameters a and c, interplanar distance d, thickness and intensity of the films.

.
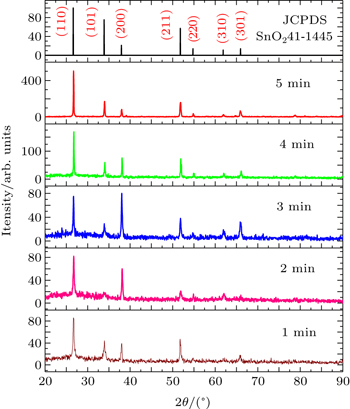
Fig. 1. Plot of film thickness versus deposition time for estimating growth velocity.
3.2. Structural properties

To investigate the crystalline quality of the films with various deposition times, XRD analysis is made. The resulting spectra are shown in Fig. 2. The analyses of these patterns reveal that the SnO2 film is of polycrystal with a tetragonal rutile phase of tin oxide (JCPDS card No.041-1445), which belongs to the space group P42/mnm (number 136). It is perceptible from the XRD patterns of Fig. 2 that the matching of the observed values with standard ‘d’ values confirms that the deposited film is of SnO2 film with a cassiterite tetragonal structure.

Fig. 2. X-ray diffraction patterns of SnO2 thin films with different film thickness values.

The (110) is the most intense peak which is observed for all samples, and other peaks assigned as (101), (200), (211), (220), (310), and (301) orientations are also observed with increasing film thickness. This can be attributed to the density of the atoms in the (110) plane, which is the highest in the atom densities in all planes of the rutile crystal structure; therefore, the surface energy of the (110) plane is the lowest.

The reflection intensity for each peak contains information about the preferential or random growth of polycrystalline thin films, which is investigated by calculating the texture coefficient TC(hkl) for the plane from the following equation:[15]

where I(hkl) is the measured intensity of x-ray reflection, and N is the number of reflections observed in the XRD pattern. The calculated TC values are presented in Fig. 3 where the variations of the texture coefficient with the deposition time for each peak are depicted. A sample with randomly oriented crystallite presents TC(hkl) = 1. The larger this value is, the larger the abundance of crystallites are oriented in the (hkl) direction.[16] In all films, TC values of (110) peak continuously increase with thickness growing, this phenomenon can be attributed to the decrease in the density of oxygen vacancies in the film, caused by a few defects relating to the growth along the (110) plane.

Fig. 3. Variations of TC values with film thickness.

The intensity of thin film can be estimated from the following equation:

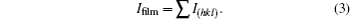
The calculated intensities of thin films are presented in Table 1. The intensity of thin film increases with film thickness increasing. This is may be attributed to the increase in the amount of sprayed tin due to the increase of deposition time.[17]

The lattice constants a and c for tetragonal phase structure are determined from Eq. (4):[18]

where d is the interplaner distance; h, k, l are Miller indices. The calculated d values and standard lattice constants are given in Table 1. The calculated a and c values are slightly higher than those given in JCPDS card No: 41-1445 (a0 = b0 = 4.7382 Å, c0 = 3.1871 Å).

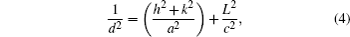
The grain sizes of the films are calculated from the highly textured (110) peaks from the Scherer formula:[19]

where D is the grain size of nano-particle, β is the full width at half of the peak maximum (FWHM) in radian and θ is the Bragg angle. The grain size values for (110) peaks are presented in Fig. 4. For the (110) peak, the calculated D value continuously increases from 32.93 nm to 56.88 nm with the increase of deposition time, indicating the improvement in crystallinity of the film.

Fig. 4. Variations of grain size, strain and dislocation density with film thickness.

The misfit strain is one of the most important factors adversely affecting the structural properties, which results from the geometric mismatch at inter phase boundaries between crystalline lattices of films and substrate.[20] These stresses can cause strains in the films. The strain (ɛ) value of SnO2 film for the (110) peak is calculated from the following formula:[21]

where β is the full-width at half-maximum of the preferential peak; the calculated values for (110) peak are given in Fig. 4. It is observed that the strain decreases with the increase of deposition time.

The dislocation density (δ) is defined as the length of dislocation line per unit volume (lines/m2). For the (110) peak, the dislocation density (δ) of the film is estimated from the following equation:[22]

For the (110) peak, the greater value of δ is calculated to be as high as 9.22 × 1014 lines/m2 for 1-min time deposition, and the smallest value as low as 3.09 × 1014 lines/m2 for 5 min time deposition.

Figure 4 shows the variations of grain size, strain and dislocation density with film thickness. We note an inverse relationship between the crystal size and dislocation density. This explains the dislocation density contribution to the smash grain. It is noted that the strain has an inverse variation to that of the grain size, due to the corresponding increase of the grain boundaries.

Figure 5 shows the AFM topographies of 5 specimens. It can be seen that each film presents a uniform morphology with small grain and low surface roughness. The crystallinity of the film improves and the crystallite size becomes larger with deposition time increasing. This result agrees well with XRD data shown in Fig. 2.

Fig. 5. Atomic force microscope (AFM) surface images of SnO2 films with different thickness values.
3.3. Optical properties

Optical properties of SnO2 thin films are investigated by UV–VIS spectrophotometer at room temperature.

Figure 6 shows optical transmittance curves each as a function of wavelength for the SnO2 thin films. Each of these films has an average transmittance greater than 65% in the visible region. As the thickness increases, the average transmittance of the film increases as the thickness increases from 550 nm to 730 nm, and then decreases at greater values of the film thickness. Further, the absorption edge of 2-min deposition sample does shift towards the longer wavelengths, however, the absorption edges of 4-min and 5-min deposition samples in fact have the blue shift.

Fig. 6. Optical transmittances versus wavelength for SnO2 films with different thickness values.

In order to find the band gap (Eg) values of films, initially the absorption coefficient (α) should be identified by the relation:[23]

where T is the transmittance and t is the film thickness. The optical band gap of SnO2 thin film is obtained from the following relation:[24]

where hv and A are photon energy and a constant, respectively. The Eg value is determined by plotting (αhv)2 versus (hv) and extrapolating the linear region of the plot to zero absorption ((αhv)2 = 0).

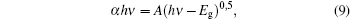
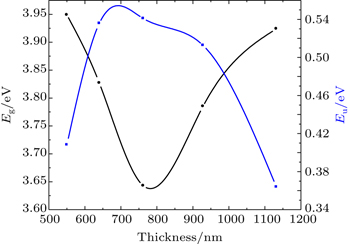
The film thickness effect on the absorption measurement is investigated. As seen from Table 2, the band gap decreases from 3.94 eV to 3.64 eV when the thickness increases from 550 to 730 nm, and then widens at a greater thickness of the film, which is in good agreement with the reported values of band gap obtained for SnO2 prepared by spray pyrolysis technique.[25]

Table 2.

Values of optical parameters of SnO2 thin films.

.

The localised states near the band edge cause the band tails to occur in material band diagram. These band tail states are responsible for the absorption in the low energy range. In this range the absorption coefficient is given as:[26]

where α0 is the pre-exponential factor, hv the photon energy, and EU the band tail width or energy of disorder commonly called an Urbach tail.[26] EU can be estimated from the inverse slope of the linear plot between ln(α) versus (hv).

Figure 7 shows the variations of band gap and Urbach tail each as a function of film thickness. We can easily observe that the band gap decreases as the thickness increases from 550 nm to 760 nm, and then widens at a greater thickness of the film. The decreasing of the band gap with increasing film thickness can be attributed to the improvement in crystallinity, morphological change, changes of atomic distance and grain size. In the growth process some impurity (oxygen vacancies and/or Sn interstitials, etc.) levels appear near the conduction band with increasing film thickness.[27] There is a possibility of structural defects appearing in the film due to their preparation conditions; this could give rise to the allowed states near the conduction band in the forbidden region. These allowed states may merge with the conduction band with increasing film thickness, resulting in the reduction of the band gap. Also the broadening effect in the band gap may refer to the decrease in the band tail width. These results agree well with XRD data shown in Fig. 2 and Refs. [27] and [28].

Fig. 7. Variations of band gap and Urbach tail with film thickness.

The refractive index (n) of semiconducting material is very important in the determining of their optical properties. Knowledge of (n) is essential in the design of heterostructure lasers, in optoelectronic devices, as well as in solar cell applications. The refractive index of the film can be calculated from the following Herve and Vandamme relation:[29,30]

where A and B are numerical constants with values of 13.6 eV and 3.4 eV respectively. The variations of refractive index (n) with film thickness are shown in Table 2. The refractive index values lie between 2.105 and 2.175 with increasing film thickness. Since n is strongly related to band gap energy, it can be concluded that the smaller band gap energy material has a larger value of refractive index.

The porosity is the property of a material with small-size pores or cavities which can contain fluids (liquid or gas). The volume porosity p(%) of the film is estimated from the refractive index n by using the Lorentz–Lorentz relationship:[31]

where N = 2,[32] the calculated volume porosity values of thin films with different thickness values are presented in Table 2 which are in good agreement with the reported values of volume porosity obtained for SnO2 prepared by vacuum evaporation.[33]

From Table 2, it can be seen that the optical transmittances at different wavelengths increase with the increase of the film thickness, and they reach their maximal values when the film thickness is 76 nm. Hereafter, the optical transmittances decrease with the increase of the film thickness. That the increasing of transmittance with thickness is discrepant with the Beer–Lambert law[34] may be explained through changing the porosity value. The transmittance and porosity values are compatible. The porosity increases the proportion of light transmittance despite the increase in thickness.

The change in the porosity can be explained by the fact that in the first case the particles arriving at the substrate spread easily on the substrate; therefore, a denser layer is formed. When the deposition time is increased, the arriving droplets must spread on the surface of the film deposited already and discrete particles are formed, which increases the roughness and leads to a more porous morphology.

3.4. Electrical properties

The electrical properties of SnO2 films are investigated by the four-point probe method and it is found that all samples have n-type conductions. The values of sheet resistance and resistivity of the films are given in Table 3.

Table 3.

Values of electrical parameters of SnO2 thin films.

.

For measuring the sheet resistance (Rsh) by the linear four-point probe technique, the current (I) is applied between the outer two leads and the potential difference (V) across the inner two probes is measured. Since negligible contact and spreading resistance are associated with the voltage probes, one can obtain a fairly accurate estimation of Rsh from the following relation:

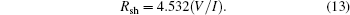
In the above configuration, a correction factor of 4.532 is used for all samples. The sheet resistances of our films are between 205.27 Ω and 325.25 Ω, which are consistent with the reported values of sheet resistance obtained for SnO2 prepared by spray pyrolysis technique.[35]

The resistivity values of SnO2 films are calculated from the following formula:

The resistivity continuously increases from 0.01125 Ω·cm to 0.03405 Ω·cm with the increase of film thickness.

The tin oxide is widely used in solar cells as a front contact material. To determine the efficiency of SnO2 in usage as a front contact, the figure of merit parameter is built up by Haacke as follows:[36]

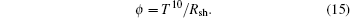
The figure-of-merit values of films with different thickness values in the present study are calculated by Eq. (15), and the results are shown in Table 3. It is found that the film deposited at 3 min (760-nm thick) has the highest figure-of-merit value (1.15 × 10−4 Ω−1). This is possible due to the formation of a good-quality film in the senses of conductivity and transmittance.

It is clear that the resistivity increases with increasing film thickness. The resistivity variation is attributed to carrier concentration and/or mobility changing. These parameters are closely related to the film structure. The SnO2 grains are relatively closely distributed on the surface and they grow along the densest plane of the rutile structure, which causes the carrier density to reach a lowest value and/or the electron traps to increase with film thickness increasing.

4. Conclusions

Polycrystalline thin films of SnO2 with different thickness values are prepared at 500 °C on glass substrates using a home-made spray pyrolysis apparatus. The influence of thickness on the film physical properties is investigated by using XRD, AFM, four-point and UV-vis spectrophotometer measurements. Film thickness values are estimated by the gravimetric method to be between 550 nm and 1130 nm. XRD characterization reveals that the SnO2 films are of polycrystals each with a cassiterite tetragonal crystal structure and preferential orientation along the (110) plane. From electrical measurements, it is found that the film has n-type electrical conductivity; a maximum figure-of-merit value (as high as 1.15 × 10−4 Ω−1) is obtained for SnO2 thin film with 760-nm thickness. All films have high transmissions greater than 65% in the visible region, indicating that they are good-quality films. The highest refractive index and optical band gap values are also found to be 2.175 eV and 3.64 eV, respectively, for the sample deposited at a deposition time of 3 min.

From these results, it is concluded that favorable structural, electrical and optical properties of SnO2 thin films make them a very suitable candidate for usage in optoelectronic devices and solar cell applications.

Reference
1Kikuchi NKusano EKishio EKingara A 2002 Vacuum 66 365
2Man-Soo HLee H JJeong H SSeo Y WKwon S J2003Surf. Coat. Technol.29171
3Matsubara KFons PIwata KYamada ASakurai KTampo HNiki S2003Thin Solid Films431369
4Wohlmuth WAdesida I 2005 Thin Solid Films 479 223
5He HJrWu T HHsin C LLi K MChen L JChueh Y LChou L JWang Z L 2006 Small 2 116
6Cao HQiu XLiang YZhang LZhao MZhu Q2006Chem. Phys. Chem.7497
7Thangaraju B 2002 Thin Solid Films 402 71
8Abass A K1987Solid State Commun.1507
9Chopra K LMajor SPandya D K 1983 Thin Solid Films 102 1
10Chaudhuri U RRamkumar KSatyam M 1990 J. Phys. D: Appl. Phys 23 994
11Afify H HTerra F SMomtaz R S 1996 J. Mater. Sci: Materials in Electronics 7 149
12Elangovan ESingh M PRamamurthi K 2004 Mater. Sci. Eng. 113 143
13Elangovan ERamamurthi K 2005 Thin Solid Films 476 231
14Thangaraju B 2002 Thin Solid Films 402 71
15Benouis C EBenhaliliba MYakuphanoglu FTiburcio Silver AAida M SSanchez Juarez A 2011 Synthetic Metals 161 1509
16Caglar MCaglar YIlıcan S2006J. Optoelectron. Mater.81410
17Elangovan ERamamurthi K 2005 Appl. Surf. Sci. 249 183
18Chacko SPhilip N SGophandran K GKoshy PVaidyan V K 2008 Appl. Surf. Chem. 254 2179
19Kasar R RDeshpande N GGudage Y GVyas J CRamphal S 2008 Physica 403 3724
20Bedir MOztas MBakkaoglu O FOrmanel R2005Eur. Phys. J. B5465
21Ashraf MAkhtar S M JKhan A FAli ZQayyum A 2011 J. Alloys Compd. 509 2414
22Ravichandran KMuruganantham GSakthivel B 2009 Physica 404 4299
23Tauc JGrigorovici RVancu A 1966 Phys. Status Solidi 15 627
24Keskenler E FTurgut GDogan S 2012 Superlattices and Microstructures 52 107
25Turgut GErdal S 2014 Superlattices and Microstructures 69 175
26Urbach F1953Phys. Rev.921324
27Ali Yıldırım MAytunç A 2010 Opt. Commun. 283 1370
28Benhaoua BAbbas SRahal ABenhaoua AAida M S 2015 Superlattices and Microstructures 83 78
29Mezrag FMohamed W KBouarissa N 2010 Physica 405 2272
30Herve PVandamme L K J 1994 Infrared Phys. Technol. 35 609
31Born MWolf E1975Principle of OpticsNew YorkPergamon85
32Chatelon J PTerrier CRoger J A 1999 Semicond. Sci. Technol. 14 642
33Sefardjella HBoudjema BKabir ASchmerber G 2013 J. Phys. Chem. Solids 74 1686
34Rahmane SAida M SDjouadi M ABarreau N 2015 Superlattices and Microstructures 79 148
35Memarian NRozati S M2012Acta Physica Polonica A122202
36Babar A RShinde S SMoholkar A VBhosale C HKim J HRajpure K Y 2010 J. Alloys. Compd. 505 416