† E-mail:
‡ Corresponding author. E-mail:
§ E-mail:
¶ E-mail:
Project supported by the Funds from the Ministry of Education, Science and Technological Development of the Republic of Serbia (Grant No. 45005). Z. L. Mišković thanks the Natural Sciences and Engineering Research Council of Canada for Finacial Support.
We investigate the interactions of charged particles with straight and bent single-walled carbon nanotubes (SWNTs) under channeling conditions in the presence of dynamic polarization of the valence electrons in carbon. This polarization is described by a cylindrical, two-fluid hydrodynamic model with the parameters taken from the recent modelling of several independent experiments on electron energy loss spectroscopy of carbon nano-structures. We use the hydrodynamic model to calculate the image potential for protons moving through four types of SWNTs at a speed of 3 atomic units. The image potential is then combined with the Doyle–Turner atomic potential to obtain the total potential in the bent carbon nanotubes. Using that potential, we also compute the spatial and angular distributions of protons channeled through the bent carbon nanotubes, and compare the results with the distributions obtained without taking into account the image potential.
Soon after the discovery of carbon nanotubes, several groups started investigating interactions of charged particles with nanotubes. A number of theoretical papers have focused on ion channeling with the main aim to explore the possibility of guiding ion beams with carbon nanotubes.[1–14] However, the experimental studying of ion channeling through carbon nanotubes is still in its beginning.[15,16] Zhu et al.[15] obtained the first experimental data on ion channeling through nanotubes with He+ ions of the kinetic energy of 2 MeV and an array of the well-ordered multi-wall carbon nanotubes grown in a porous anodic aluminum oxide (Al2O3) membrane. The authors measured and compared the yields of ions transmitted through the bare Al2O3 sample and those through the Al2O3 sample including the nanotubes. Chai et al. obtained the first experimental data with electrons and nanotubes.[16] They used the 300-keV electrons and studied their transport through the multi-wall carbon nanotubes of the length in a range of 0.7 μm–3.0 μm, embedded in a carbon fiber coating. Nevertheless, this field of research still remains attractive.[17,18]
An ion in the MeV energy range will induce a strong dynamic polarization of the valence electrons in carbon atoms. This will give rise to a sizeable image force on the ion, as well as a considerable energy loss due to the collective, or plasma, excitations of those electrons.[15–17] Calculations of the image force in Refs. [19]–[21] were based on a two-dimensional (2D), one-fluid hydrodynamic model, which treats all four valence electrons in carbon atoms as a single fluid of quasi-free charges that occupy the surface of a cylinder. It was shown that the dynamic polarization effect exerts a large influence in the angular distributions of protons channeled through a short and straight (11, 9) SWNT.[19–21]
However, in the ion channeling experiments, there is always a question about the curvature of carbon nanotubes, because in reality carbon nanotubes are seldom perfectly straight. There are some studies of channeling through the bent carbon nanotubes, but without taking into account the image force.[22–24] So, it is important to study the influence of dynamic polarization of carbon nanotubes when the nanotubes are curved. Therefore, in this paper, we extend our investigation of the spatial and angular distributions of the channeled ions[19–21] to the cases in which the carbon nanotubes are not straight. We evaluate the dynamic image potential for ions by means of an extended two-fluid hydrodynamic model. Unlike our previous work, where valence electrons in carbon were treated as a quasi-free charged fluid with zero damping,[19–21] in the present work we use an extended version of the hydrodynamic model, where π and σ electrons in the nanotube wall are treated as two charged fluids, each with its own restoring frequency and damping factor.[25] Such an extension of the hydrodynamic model with suitably chosen parameters showed great success and versatility in the recent modelling of several independent experiments involving electron energy loss spectra (EELS) of different carbon nanostructures. Specifically, the extended two-fluid hydrodynamic model was used to explain the experimental spectra in high-energy EELS of single- and multi-layer graphene,[26] single-walled carbon nanotubes,[27] and individual C60 molecules,[28] as well as the low-energy reflection EELS of single-layer graphene supported by a metal substrate.[29] While the trajectories of charged particles in those studies were either traversing or obliquely incident on carbon nanostructures, the present work presents our first application of the extended hydrodynamic model under channeling conditions. We use the dynamic image potential from the extended hydrodynamic model in a Monte Carlo (MC) type of computation to obtain the spatial and angular distributions of protons moving at a speed of v = 3 a.u. through the bent (6, 4), (8, 6), (11, 9), and (15, 10) SWNTs. By comparing those results with the distributions obtained without the image potential, we are able to give a preliminary assessment of the influence of the image potential on the distribution of ions channeled through the bent carbon nanotubes.
We first present the basic theory used in our modeling of proton channeling, then we discuss the results for spatial and angular distributions, and we finally give our concluding remarks. Atomic units are used throughout unless otherwise explicitly stated.
We model an SWNT as an infinitesimally thin cylindrical shell with radius R and length L, and assume that the valence electrons in the ground state may be considered as an electron gas distributed uniformly over a cylindrical surface, with a number density per unit area 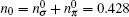
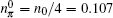
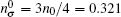
Following Ref. [30], one may express the self-energy, or the image potential Uim, experienced by a point-charge ion Q on the trajectory
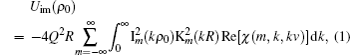
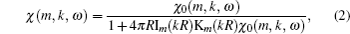

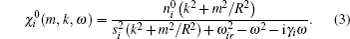
In the present paper we also compute spatial and angular distributions of protons channeled through a bent SWNT with and without including the image force. The initial proton velocity is chosen to be 3 a.u. (corresponds to the energy 0.223 MeV) and it is taken to be parallel to the z axis. Numerical calculation is performed in a Cartesian coordinate system with the z axis that coincides with the nanotube axis and with the origin that lies in its entrance transverse plane. We assume that the nanotube is sufficiently short, for the proton energy loss is neglected, but is long enough so that we can omit the effect of nanotube ends on the image potential. The nanotube length of L = 0.2 μm is considered to satisfy both these requirements.[19]
For the short-ranged proton interaction with carbon atoms in the nanotube wall, we use the repulsive Doyle–Turner potential (averaged axially and azimuthally over the nanotube wall),[3,32,33] which gives
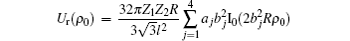
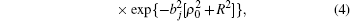
We assume that the nanotube is bent along the positive direction of the y axis. Its bending angle is α = 4 mrad. The channeling mechanism in bent carbon nanotubes may be considered in a frame of reference that rotates around a center with the bending radius Rb of a nanotube. This means that the new reference frame rotates in the yz plane along the circle of radius Rb = L/α that is the radius of curvature of the nanotube.[23,24] This is a non-inertial reference frame in which one need to treat the nanotube as if it were straight and use the effective proton-nanotube interaction potential
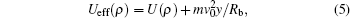
The dynamic polarization of the nanotube by the proton is treated using the 2D extended two-fluid[25,27] hydrodynamic model of the carbon valence electrons, which is based on a jellium-like description of the nanotube ion cores. Therefore, our model for the attractive image potential given by Eq. (
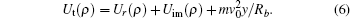
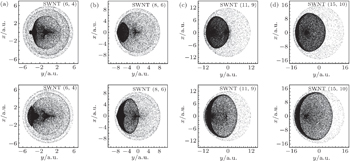
The angular and spatial distributions of the channeled protons in the exit transverse plane are generated using a Monte Carlo computer simulation method.[19] The initial proton position, x0 and y0, is chosen randomly from a 2D uniform distribution with the condition 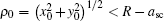
In the case of a straight nanotube the critical angle for channeling is 
In addition, in the case of proton channeling through a nanotube it is important to stress two facts, which justify our use of the continuum approximation in Eq. (
In order to justify the zero-thickness approximation for the σ and π electrons, one should consider the following facts. Compared with the π electrons, the σ electrons are more localized within the hexagonal lattice of the nanotube wall, whereas the π electron orbitals are localized within a range of about 0.1 nm on that wall. On the other hand, typical distances of turning points from the nanotube wall in the trajectories of channeled protons are expected to be larger than the size of the π electron orbital. For example, in Fig.
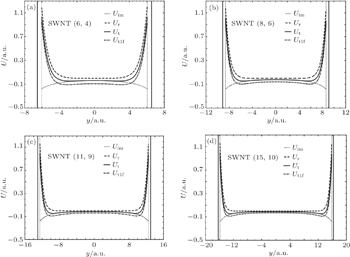
In this section we first analyze the total potentials in four different nanotube types[36,37] in the presence of the image potential calculated from both the one-fluid and the extended two-fluid hydrodynamic models.[25,31] We then present and discuss the effects of the image potential from the extended two-fluid model on the spatial and angular distributions of the protons channeled through both the straight and bent nanotubes. In our analysis we assign the fixed values to several important parameters: proton speed v = 3 a.u., nanotube length L = 0.2 μm and, in the case of bent nanotubes, bending angle α = 4 mrad.
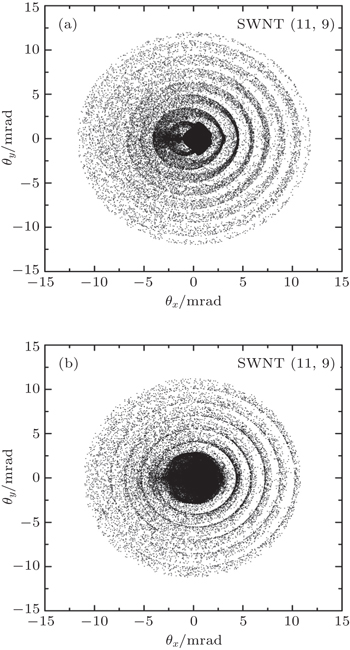
Figure
Figure
From Figs.
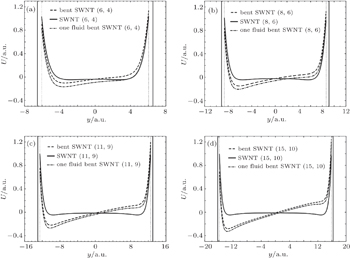
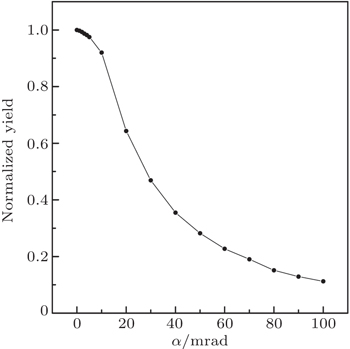
Figure
Figure
Figure
Figure
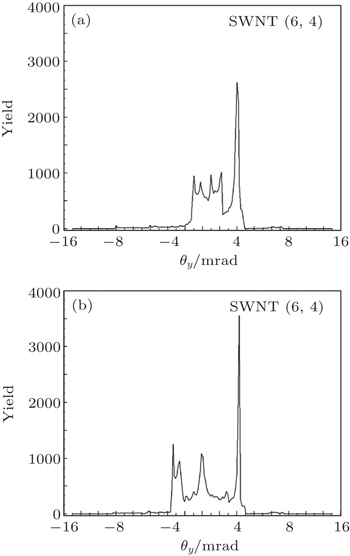
Figures
In Fig.
Next, we provide the main reasons for choosing the values of proton energy and the nanotube lengths in this work.
Future developments in our work will be concerned with simulations for longer nanotubes that include the effects of energy loss of channeled protons and the angular uncertainty because of the proton collisions with the nanotube electrons in the presence of the dynamic polarization of the nanotube electrons.
In this work, we study the channeling of protons that move at a speed of 3 a.u. through four different types of straight and bent SWNTs, namely (6, 4), (8, 6), (11, 9), and (15, 10). The effects of dynamic polarization of the valence electrons in the nanotube wall are assessed by both the one-fluid hydrodynamic model and an extended two-fluid hydrodynamic model. According to those models, we calculate the image potential for protons and combine it with the Doyle–Turner repulsive potential to obtain the total potentials in the straight and bent carbon nanotubes respectively. We then calculate individual proton trajectories by solving the classical equation of motion in a total potential based on the image potential from the extended two-fluid model. Finally, a Monte Carlo (MC) code is used to compute the spatial and angular distributions of protons channeled through short and bent nanotubes respectively. In the MC code we use the parameters for the extended two-fluid hydrodynamic model, which were determined in recent applications in the modelling of several independent experiments on electron energy loss spectra of different carbon nanostructures.[31] Therefore, compared with our previous studies of the image potential effects in ion channeling that were based on a one-fluid model with zero damping for a quasi-free electron gas in nanotubes, this work provides a complete and accurate description of the dynamic polarization effects.
The results show that the presence of the image potential in a bent nanotube broadens and deepens the attractive potential well, which happens in each nanotube due to the centrifugal force in a non-inertial frame of reference for proton motion. As a consequence, the spatial distributions of the channeled protons in the presence of the image potential are generally broader in the directions that are parallel and perpendicular to the bending plane of all four types of nanotubes. Angular distributions also exhibit broadening, but to a lesser extent than the spatial distributions, which is accompanied with a significant redistribution of the proton flux that follows the nanotube bending angle. Overall, there is a tendency for the image potential to increase both the proton yield in the spatial distributions and the proton flux in the angular distributions, in the peripheral regions of the nanotubes, away from the bending center.
All our findings indicate that the influence of the dynamic polarization on ion channeling through bent carbon nanotubes in the MeV energy range is strong and it should not be omitted in simulations. In particular, the presence of the image potential may diminish the bending efficiency of carbon nanotubes for charged particles that move in the range of speeds of several Bohr velocities.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 |