Cite this Article
Luo Wen-Yu, Yu Xiao-Lin, Yang Xue-Feng, Zhang Ren-He. Analytical solution based on the wavenumber integration method for the acoustic field in a Pekeris waveguide. Chinese Physics B, 2016, 25(4): 044302  
Permissions
Analytical solution based on the wavenumber integration method for the acoustic field in a Pekeris waveguide
Luo Wen-Yu1, †, , Yu Xiao-Lin1, 2, Yang Xue-Feng2, 3, Zhang Ren-He1
State Key Laboratory of Acoustics, Institute of Acoustics, Chinese Academy of Sciences, Beijing 100190, China
University of Chinese Academy of Sciences, Beijing 100049, China
Shanghai Acoustic Laboratory, Chinese Academy of Sciences, Shanghai 200032, China

 

† Corresponding author. E-mail: lwy@mail.ioa.ac.cn

Project supported by the National Natural Science Foundation of China (Grant No. 11125420), the Knowledge Innovation Program of the Chinese Academy of Sciences, the China Postdoctoral Science Foundation (Grant No. 2014M561882), and the Doctoral Fund of Shandong Province, China (Grant No. BS2012HZ015).

Abstract
Abstract

An exact solution based on the wavenumber integration method is proposed and implemented in a numerical model for the acoustic field in a Pekeris waveguide excited by either a point source in cylindrical geometry or a line source in plane geometry. Besides, an unconditionally stable numerical solution is also presented, which entirely resolves the stability problem in previous methods. Generally the branch line integral contributes to the total field only at short ranges, and hence is usually ignored in traditional normal mode models. However, for the special case where a mode lies near the branch cut, the branch line integral can contribute to the total field significantly at all ranges. The wavenumber integration method is well-suited for such problems. Numerical results are also provided, which show that the present model can serve as a benchmark for sound propagation in a Pekeris waveguide.

PACS: 43.30.Bp;43.20.Bi
Keyword:wavenumber integration technique;Pekeris waveguide;analytical solution;branch line integral
1. Introduction

A solution of the acoustic field in a homogeneous ocean channel overlying a homogeneous fluid halfspace was proposed in a classic paper by Pekeris[1] over half a century ago. Because the problem of sound propagation in a Pekeris waveguide is of considerable practical importance, many researchers have investigated this problem since then.[2–4]

The normal mode method is very important in underwater acoustics, for which the most important component consists of the trapped modes, which are evanescent in the lower halfspace. The form of the non-trapped part of the modal solution depends on the choice of the branch cut related to the sound speed in the homogeneous lower halfspace. When the Pekeris branch cut[5] is chosen, the remainder of the field consists of the Pekeris branch line integral (PBLI) and an infinite set of leaky modes, which decay exponentially with range and propagate in the lower halfspace. When the EJP cut[5] is chosen, the remainder of the field is the EJP branch line integral (EBLI) alone. Thus, the total field can be written as[6]

where TM and LM represent trapped and leaky modes, respectively.

For a numerical normal mode model to obtain the exact field, either of the branch line integrals should be computed.[7–9] However, since the significance of the branch line integral diminishes with range, traditional normal mode models usually neglect this integral, thus yielding solutions which are not valid at short ranges. Note that under certain circumstances the contribution of the branch line integral can be significant at all ranges. For instance, when a mode lies near the branch cut, the branch line integral is important at all ranges. Obviously, traditional normal mode models cannot provide accurate field results in this case. Special treatment is required to obtain accurate field results. One approach is to obtain a discrete approximation to the continuous spectrum by introducing an artificial pressure-release lower boundary. This approach is combined with the Galerkin method to compute the local modes in COUPLE,[10] which is also adopted in DGMCM.[11] However, the improvement in accuracy for COUPLE and DGMCM is achieved at the cost of involving much more normal modes than would normally be required. An alternative approach is to eliminate the branch cut and replace the Pekeris branch cut by a series of modes by inserting small attenuation and sound speed gradients in the lower halfspace.[6]

The principle of wavenumber integration was introduced into underwater acoustics by Pekeris.[1] The Fast Field Program[12] developed by DiNapoli is a highly efficient wavenumber-integration-based model. Later, Schmidt[13] developed another wavenumber-integration-based model which applies the direct global matrix approach.

Reference [14] presents a wavenumber integration solution for the acoustic field in a Pekeris waveguide excited by a point source. This solution is theoretically exact. However, it is numerically unstable in that the linear equation for the amplitudes of the homogeneous solution of the depth-dependent wave equation is ill-conditioned for the horizontal wavenumber in the evanescent spectrum. Noticing this problem, reference [5] presents another solution. Unfortunately, the linear equation in this solution is still unstable. To entirely solve this problem, this paper proposes an unconditionally stable solution.

In addition to the unconditionally stable numerical solution, an exact solution involving an analytical solution for the depth-dependent Green’s function in a Pekeris waveguide is also proposed and implemented in a numerical model. Since no approximations have been introduced, this model can provide exact field solutions for a Pekeris waveguide problem with either a point source in cylindrical geometry or a line source in plane geometry.

An outline of the remainder of the paper is as follows. Section 2 first considers the point-source, Pekeris waveguide problem and presents an unconditionally stable numerical solution for the depth-dependent Green’s function, followed by an analytical solution. Details of the evaluation of the wavenumber integral and the transmission loss are also provided. The solution for the line-source, Pekeris waveguide problem is also given. Section 3 provides several numerical examples and results by the present model, KRAKEN,[15] and DGMCM. In Section 4 we summarize our conclusions.

2. Theory

In this section we first deal with the Pekeris waveguide problem with a point source in cylindrical geometry, and then solve the problem with a line source in plane geometry.

2.1. Point source problem

Consider the problem of sound propagation excited by a point source of strength Sω in a Pekeris waveguide involving a homogeneous water column of depth D, sound speed c1, and density ρ1, overlying a homogeneous fluid halfspace of sound speed c2, density ρ2, and attenuation α2. A schematic of this problem is shown in Fig. 1. A cylindrical coordinate system is chosen, with the vertical z axis passing through the source and the r axis being parallel with the sea surface. The location of the source is denoted by (0, zs). For this problem, the two-dimensional (2D) Helmholtz equation for the displacement potential ψ(r,z) takes the form[5]

With the following Hankel transform pair,

the depth-dependent wave equation can be shown to be

where .

Fig. 1. Schematic diagram of the Pekeris-waveguide problem. The amplitudes of the down- and upgoing waves in water and that of the downgoing wave in the bottom in the homogeneous solution to the depth-dependent wave equation are denoted by , , and , respectively.

The depth-dependent Green’s function, Ψ(kr,z), can be computed either numerically or analytically. In the subsequent sections we will give these two solutions separately.

2.1.1. Numerical solution for the depth-dependent Green’s function

Below we first show briefly that the solution to Eq. (4) as given in Ref. [14] is numerically unstable. Then we show that the solution given in Ref. [5] still does not solve this stability problem. Subsequently, we propose an unconditionally stable numerical solution to Eq. (4).

In Ref. [14], the depth-dependent Green’s function in water (0 ≤ z ≤ D) is represented by

where , with k1 denoting the water wavenumber at frequency ω. In this paper, the properties in water and those in the bottom are indicated by the subscripts 1 and 2, respectively. In the bottom (z > D), the depth-dependent Green’s function is represented by

where kz,2 is the vertical wavenumber in the bottom defined as follows to satisfy the radiation condition for z → ∞,

with k2 denoting the bottom wavenumber at frequency ω. The amplitudes , , and are to be determined by the boundary conditions, as shown below.

By imposing the boundary conditions of vanishing pressure at the sea surface, the continuity of the normal particle displacement at the bottom, and the continuity of pressure at the bottom, we reach the following linear system of equations for the amplitudes of the homogeneous solution to Eq. (4),[14]

The above linear system of equations is theoretically correct. However, as pointed out in Ref. [5], numerical instability will occur in the evanescent regime kr > k1 when equation (8) is solved by a standard equation solver. The reason is that as kr > k1, we have

where β > 0, yielding that as βD → ∞, exp(ikz,1D) = exp(−βD) → 0 whereas exp(−ikz,1D) = exp(βD) → ∞. Thus, due to inappropriate normalization of the “upgoing” wave in water in Eq. (5), the resulting system of equations is ill-conditioned.

Noticing the above-mentioned stability problem in Ref. [14], reference [5] gives another system of equations for the amplitudes , , and of the homogeneous solution to the depth-dependent wave equation in Eq. (4). Unfortunately, as shown below, the system of equations given in Ref. [5] is still numerically unstable.

In Ref. [5], the depth-dependent Green’s function in water is represented by

whereas the expression for the depth-dependent Green’s function in the bottom remains the same as that in Eq. (6). By imposing the boundary conditions, we reach the following linear system of equations for the amplitudes , , and :[5]

which is exactly Eq. (2.184) in Ref. [5]. It is obvious that the terms containing the exponentially growing term exp(−ikz,1D) for kr in the evanescent spectrum are still present in this system of equations. For the same reason, this system of equations is also numerically unstable.

As shown above, although both the linear system of equations in Eq. (8) as given in Ref. [14] and that in Eq. (10) as given in Ref. [5] are theoretically exact, neither of them is numerically stable. The reason is that neither of these two formulations normalizes the “upgoing” wave in water appropriately. Below we propose an unconditionally stable linear system of equations for the amplitudes , , and , which is simply achieved by using the seabed, rather than the sea surface, as the origin for the exponential function representing the “upgoing” wave in water. Thus, the depth-dependent Green’s function in water is represented by

whereas the expression for the depth-dependent Green’s function in the bottom remains the same as that in Eq. (6).

By imposing the boundary conditions, we obtain the following linear system of equations

From Eq. (12) we can see that all the exponentially growing terms for kr in the evanescent regime have been eliminated. As a result, this system of equations is unconditionally stable and hence can be solved by a standard linear system solver.

Once the amplitudes , , and are obtained by solving Eq. (12), the depth-dependent Green’s function can then be evaluated by Eqs. (11) and (6) at discrete horizontal wavenumbers at the receiver depth. Then the displacement potential ψ(r,z) can be computed by evaluating the inverse Hankel transform given in Eq. (3b). The displacement potential thus obtained is exact, except for minor accuracy sacrificed in evaluating the integral in Eq. (3b), which is generally negligible.

2.1.2. Analytical solution for the depth-dependent Green’s function

In the previous section we propose an unconditionally stable numerical solution for the amplitudes of the homogeneous solution to the depth-dependent wave equation. As shown below, for the problem of sound propagation in a Pekeris waveguide, we can solve Eq. (12) analytically for the amplitudes , , and , yielding closed-form expressions for the depth-dependent Green’s functions in water and the bottom separately.

By solving Eq. (12) analytically, we obtain the following analytical expressions for the amplitudes of the depth-dependent wave equation:

By substituting the above analytical expressions for , , and into Eqs. (11) and (6), it can be shown that the closed-form expression for the depth-dependent Green’s function in water is

and that in the bottom is

It is obvious that the above analytical solution for the depth-dependent Green’s function in water satisfies reciprocity (the source is assumed to be located in water, as shown in Fig. 1). Besides, it can be easily shown that as ρ2 → 0, equation (14a) reduces to the depth-dependent Green’s function in water for the ideal waveguide problem involving a pressure-release sea surface and a pressure-release lower boundary,

The analytical solution for Ψ(kr,z) in this ideal waveguide is also given by Eq. (2.143) in Ref. [14] and by Eq. (2.146) in Ref. [5], viz.,[5]

However, this solution is wrong, where the factor −Sω/4π should be replaced by −Sω/2π.

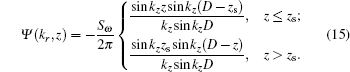
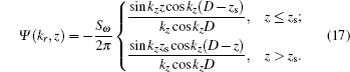
Similarly, with ρ2 → ∞, equation (14a) reduces to the depth-dependent Green’s function in water for the ideal waveguide problem involving a pressure-release sea surface and a rigid bottom,

Direct derivations of Eqs. (15) and (17) are also given in Appendix A.

In addition, with ρ1 = ρ2 and c1 = c2, it can be easily shown that equation (14a) reduces to the depth-dependent Green’s function in a fluid halfspace,[5]

2.1.3. Wavenumber integration and transmission loss

Once the depth-dependent Green’s function is obtained, the displacement potential, ψ(r,z), can be evaluated by applying the inverse Hankel transform given in Eq. (3b). Note that direct numerical evaluation of the wavenumber integral in Eq. (3b) requires very fine wavenumber sampling, which is obviously undesirable for computational reasons. To improve numerical efficiency, the complex integration contour presented in Ref. [5] is adopted is this work, with the contour offset determined by

where M is the total number of sampling points and [kmin,kmax] is the integration interval.

As shown in Ref. [5], for a specific wavenumber sampling Δk = (kmax − kmin)/(M − 1), accurate field results can only be obtained up to range R/2, where R is determined by

In this work, the transmission loss for the point-source problem is defined by

where

and the reference pressure takes the form (assuming the point source is located in water)

Since no approximations have been introduced, the acoustic field thus obtained is exact. Minor accuracy, which is generally negligible, might be sacrificed only in evaluating the wavenumber integral in the inverse Hankel transform.

2.2. Line source problem

Normally a point source is appropriate for practical problems in underwater acoustics. However, for purposes such as inter-model comparisons and further extension of a 2D model to a three-dimensional (3D) model, it is also useful to work with a line source in plane geometry.

In this section we consider the problem of sound propagation excited by a line source of strength Sω in a Pekeris waveguide involving a homogeneous water column of depth D, sound speed c1, and density ρ1, overlying a homogeneous fluid halfspace of sound speed c2, density ρ2, and attenuation α2. This problem can also be illustrated schematically by Fig. 1, except that the r axis should be replaced by the x axis because a Cartesian coordinate system is appropriate for the line-source problem, with the vertical z axis passing through the source and the x axis being parallel with the sea surface. The location of the source is denoted by (0, zs). For this problem, the 2D Helmholtz equation for the displacement potential ψ(x,z) takes the form[5]

With the following Fourier transform pair,

the depth-dependent wave equation can be shown to be

where

2.2.1. Analytical solution for the depth-dependent Green’s function

By comparing Eq. (26) with the depth-dependent wave equation in the point-source case, i.e., Eq. (4), we can see that the depth-dependent wave equation in the line-source problem is of the same form as that in the point-source problem, except that in the point-source problem whereas in the line-source problem. Thus, following the derivation in Subsection 2.1, we can obtain the analytical solution for the depth-dependent Green’s function for the line-source problem, which is

in water and

in the bottom.

2.2.2. Transmission loss

Once the depth-dependent Green’s function is obtained, the displacement potential, ψ(x,z), can be evaluated by applying the inverse Fourier transform given in Eq. (25b). Alternatively, we may also use the following equivalent but more numerically efficient form,

In this work, the transmission loss for the line-source problem is defined by

where

and the reference pressure takes the form (assuming the line source is located in water)

It should be pointed out that the expression for the transmission loss used in KRAKEN is different from the exact form as given above and implemented in the present model. The difference arises from the evaluation of the Hankel function. That is, the term in the exact form is not evaluated in KRAKEN to avoid the evaluation of the Hankel function. Instead, the asymptotic form of the Hankel function for k0 → ∞,

is applied. Note that in fact the above approximation is not appropriate because generally the argument k0 is not large. However, since we are only seeking a normalization we may go ahead and rewrite the term as follows:

The actual term used in the normalization in KRAKEN is . Thus, for the line-source problem, the transmission loss computed by the present model and that by KRAKEN differ by a constant, which is

Hence, to make the transmission-loss results by the present model comparable with those by KRAKEN, we need to subtract the former by TLdiff as given in Eq. (34). For instance, with frequency 20 Hz and reference sound speed 1500 m/s, the difference between the transmission-loss result by the present model and that by KRAKEN is about 7.7 dB. Note that this difference only exists in the line-source problem, but not in the point-source case.

3. Numerical examples

In this section we consider three numerical examples. The first one involves an ideal waveguide with a pressure-release sea surface and a perfectly reflecting (either pressure-release or rigid) lower boundary. The second one, which involves a Pekeris waveguide, is from Ref. [5], where only field results with a point source are provided. This paper gives both field results with a point source and those with a line source by the present model. The third example also involves a Pekeris waveguide. This example was considered in Ref. [6] to demonstrate how to eliminate the branch cut by the method presented in that paper.

3.1. Example 1: Ideal waveguide problem

In Section 2 we have shown that the analytical solution for the depth-dependent Green’s function in an ideal waveguide with a pressure-release sea surface and a pressure-release bottom presented in Ref. [5] is wrong. This paper proposes an analytical solution for the depth-dependent Green’s function in a Pekeris waveguide, which reduces to the depth-dependent Green’s function in an ideal waveguide with a pressure-release bottom as ρ2 → 0, and to that in an ideal waveguide with a rigid bottom as ρ2 → ∞. Below we validate our analytical solution through an example. The normal-mode model KRAKEN is used to provide reference solutions.

Consider the problem involving an ideal waveguide with a pressure-release sea surface and either a pressure-release or rigid bottom. The water depth is 100 m, and the sound speed and density in water are 1500 m/s and 1000 kg/m3, respectively. A point source is considered, located at depth 36 m and of frequency 20 Hz. The receiver depth is 46 m. For this problem, the convergence criterion given in Eq. (20) yields that the choice of kmin = 0m−1, kmax = 3k, and M = 1024 ensures convergence up to a range of 3 km, where k is the wavenumber in water.

Figure 2 shows the results of transmission loss for this ideal-waveguide problem, computed by the present method and KRAKEN. Also shown in this figure are the magnitudes of the depth-dependent Green’s function, computed along the complex contour with the offset from the real axis by the amount determined by Eq. (19). From Figs. 2(a) and 2(c) we can see that two propagating modes are excited for the pressure-release bottom case, whereas three propagating modes are excited for the rigid bottom case. The horizontal wavenumbers of the normal modes can also be determined as follows. For the pressure-release bottom case we have[5]

and for the rigid bottom case we have[5]

Then the horizontal wavenumber of mode n can be determined by

Thus, for the considered problem, the horizontal wavenumbers of the two propagating modes in the pressure-release bottom case can be determined by Eqs. (35a) and (36), which are approximately 0.077662 m−1 and 0.055412 m−1, respectively, corresponding to the two peaks in Fig. 2(a). Similarly, the horizontal wavenumbers of the three propagating modes in the rigid bottom case can be determined by Eqs. (35b) and (36), which are approximately 0.082290 m−1, 0.069256 m−1, and 0.029153 m−1, respectively, corresponding to the three peaks in Fig. 2(c) separately.

Fig. 2. Results by the present method and KRAKEN for the ideal waveguide problem. (a) Magnitude of the depth-dependent Green’s function at depth 46 m for the pressure-release bottom case; (b) transmission loss at depth 46 m for the pressure-release bottom case; (c) magnitude of the depth-dependent Green’s function at depth 46 m for the rigid bottom case; (d) transmission loss at depth 46 m for the rigid bottom case. In panels (b) and (d), the blue solid curves correspond to the solutions by the present method, and the red dashed curves correspond to the KRAKEN solutions.
3.2. Example 2: Pekeris waveguide problem

We now consider another example as schematically shown in Fig. 3, which involves either a point or a line source in a Pekeris waveguide of depth 100 m. The source and receiver depths are 36 m and 46 m, respectively, and the source frequency is 20 Hz. The sound speed and density in water are 1500 m/s and 1000 kg/m3, respectively; and the sound speed and density in the bottom are 1800 m/s and 1800 kg/m3, respectively. Both cases with a lossless bottom and with a lossy bottom with an attenuation of 0.5 dB/wavelength are considered. For this problem, the criterion given in Eq. (20) yields that the choice of M = 2048, kmin = 0 m−1, and kmax = 3k1 ensures accurate field results up to a range of 15 km for the present method.

Fig. 3. Pekeris waveguide problem with either a point or a line source. The bottom is either lossless or lossy with an attenuation of 0.5 dB/wavelength. The source frequency is 20 Hz.

Figure 4 shows the magnitude of the depth-dependent Green’s function along the complex contour with the offset from the real axis by the amount determined by Eq. (19). The blue solid curve corresponds to the lossless-bottom case and the red dashed curve corresponds to the lossy-bottom case. The presence of two peaks in this figure indicates that two modes are excited in this example.

Fig. 4. Magnitude of the depth-dependent Green’s function at a depth of 46 m for the 100-m deep Pekeris waveguide problem with either a lossless bottom (the blue solid line) or a lossy bottom with an attenuation of 0.5 dB/wavelength (the red dashed line). The bottom wavenumber is indicated by the green dashed line.

Results of transmission loss computed by the present method for this example with a point source and those with a line source are shown in Figs. 5 and 6, respectively. Below we show that the interference pattern in Figs. 5 and 6 arise from the interference of modes 1 and 2. The modal interference length of modes m and n with horizontal wavenumbers krm and krn can be represented as[5]

Consider the lossless case with a point source. From Fig. 4 we can obtain the horizontal wavenumbers of modes 1 and 2, which are approximately 0.06953 m−1 and 0.08042 m−1, respectively, yielding L1,2 ≈ 577.0 m. From Fig. 5(a) we obtain the average oscillating period of the first 10 periods, which is approximately 574.3 m. This implies that the interference pattern in Fig. 5(a) arises from the interference of modes 1 and 2. Similarly, it can be shown that this is also true for the remaining figures in Figs. 5 and 6.

Fig. 5. Results of transmission loss computed by the present method for the 100-m deep Pekeris waveguide problem with a point source. (a) Transmission loss at a depth of 46 m with a lossless bottom; (b) transmission loss at a depth of 46 m with a lossy bottom with an attenuation of 0.5 dB/wavelength; (c) transmission loss versus range and depth with a lossless bottom; (d) transmission loss versus range and depth with a lossy bottom with an attenuation of 0.5 dB/wavelength. The water-bottom interface is indicated by a white line in panels (c) and (d).
Fig. 6. Results of transmission loss computed by the present method for the 100-m deep Pekeris waveguide problem with a line source. (a) Transmission loss at a depth of 46 m with a lossless bottom; (b) transmission loss at a depth of 46 m with a lossy bottom with an attenuation of 0.5 dB/wavelength; (c) transmission loss versus range and depth with a lossless bottom; (d) transmission loss versus range and depth with a lossy bottom with an attenuation of 0.5 dB/wavelength. The water-bottom interface is indicated by a white line in panels (c) and (d).
3.3. Example 3: Branch cut problem

This example involves a lossless Pekeris waveguide with a water depth of 40 m. The source and receiver depths are 20 m and 40 m, respectively. The sound speed and density in water are 1500 m/s and 1000 kg/m3, respectively, and in the bottom they are 1650 m/s and 1500 kg/m3, respectively.

This example was considered in Ref. [6], which shows that at the frequencies where a mode lies near the branch cut, the branch line contribution can be significant at all ranges. Because branch line integrals are cumbersome to compute, and usually their contribution to the total field is significant only in the near field, they are generally neglected in traditional normal mode models. As a result, traditional normal mode models yield inaccurate field solutions at such frequencies. Reference [6] proposed a method to eliminate the branch cuts from the normal mode solution by inserting small attenuation and sound-speed gradients in the lower halfspace. An alternative solution to this problem is to introduce an artificial pressure-release lower boundary at an appropriate depth. For example, the coupled-mode model COUPLE[10,16] introduces an artificial pressure-release lower boundary together with an absorption layer right above this boundary, and applies the Galerkin method to compute the modal solutions. The model DGMCM[11,17] adopts the same method to compute the local modes and is used in this work to provide reference solutions. Below we will analyze this problem and give comparisons of the acoustic field between some of the above-mentioned methods.

Here we give the key parameters for the present model and DGMCM for this problem. For the present model, the convergence criterion given in Eq. (20) yields that M = 512 is sufficient to obtain convergent field results for the range interval 0 km to 1 km. For DGMCM, a pressure-release lower boundary is introduced at a depth of 800 m, with an attenuation increase from 0 to 5.0 dB/wavelength in the absorption layer with a of thickness 300 m.

Figure 7 shows the results of transmission loss versus range and frequency computed by KRAKEN with a homogeneous halfspace, DGMCM with an artificial pressure-release lower boundary, and the present method. It is evident that the field result by KRAKEN is irregular around 112 Hz, whereas the result by DGMCM and that by the present method are in excellent agreement. Below we will consider two specific frequencies, 112 Hz (indicated by the black dashed lines in Fig. 7) and 118 Hz (indicated by the white dashed lines in Fig. 7).

Fig. 7. Transmission loss versus range and frequency by (a) KRAKEN with a homogeneous halfspace, (b) DGMCM with an artificial pressure-release lower boundary, and (c) the present method. The frequencies 112 Hz and 118 Hz are indicated by the black and white dashed lines, respectively.

The depth-dependent Green’s functions at a depth of 40 m by the present method at frequencies 112 Hz and 118 Hz are shown in Figs. 8(a) and 8(c), respectively, where the bottom wavenumbers are indicated by the red dashed lines. Figures 8(b) and 8(d) show results of transmission loss versus range at a depth of 40 m for the range interval 0 km to 10 km computed by KRAKEN with a homogeneous halfspace (blue solid curves), DGMCM with an artificial pressure-release lower boundary (red dashed curves), and the present method (green dash–dotted curves) at the two specific frequencies 112 Hz and 118 Hz. At frequency 112 Hz the bottom wavenumber is approximately 0.426495 m−1, and at frequency 118 Hz the bottom wavenumber is approximately 0.449343 m−1. The horizontal wavenumbers of the first five modes by KRAKEN are given in the following Table 1. From Fig. 8(a) we can see that at frequency 112 Hz the horizontal wavenumber of mode 3 is so close to the bottom wavenumber, which is the branch point for this problem, that KRAKEN fails to find this mode (readers can refer to Table 1). As a result, as shown in Figs. 7 and 8(b), the field results by KRAKEN are inaccurate, especially in the near field, at this frequency. However, at frequency 118 Hz, figure 8(c) shows that the horizontal wavenumber of mode 3 is sufficiently far away from the bottom wavenumber such that KRAKEN succeeds in finding this mode (readers can refer to Table 1). As a result, as shown in Figs. 7 and 8(d), the field results by KRAKEN are in excellent agreement with those by DGMCM and the present method at this frequency. In addition, it is evident from Figs. 7 and 8 that the results by DGMCM and the present method are in excellent agreement throughout the whole frequency band of interest.

Fig. 8. (a) Magnitude of the depth-dependent Green’s function at a depth of 40 m at 112 Hz; (b) transmission loss at a depth of 40 m at 112 Hz; (c) magnitude of the depth-dependent Green’s function at a depth of 40 m at 118 Hz; (d) transmission loss at a depth of 40 m at 118 Hz. In panels (a) and (c), the red dashed lines indicate bottom wavenumbers. In panels (b) and (d), the blue solid curves, the red dashed curves, and the green dash-dotted curves are results by KRAKEN with an homogeneous halfspace, DGMCM with an artificial pressure-release lower boundary, and the present method, respectively.
Table 1.

Horizontal wavenumbers of the first five modes computed by KRAKEN.

.

Finally, we illustrate the convergence criterion regarding wavenumber sampling, M, for the present method through this example with a line source at 118 Hz. At this frequency, from the criterion given in Eq. (20), the values of M and the corresponding maximum ranges with accurate field results are given in Table 2. The field results at a of depth 40 m with different values of M are shown in Fig. 9, from which we can see that to obtain accurate field results up to 10 km, at least 5120 sampling points should be used.

Fig. 9. Illustration of the convergence criterion regarding the number of sampling points.
Table 2.

Number of sampling points and corresponding maximum range with accurate field results.

.
4. Conclusion

An unconditionally stable method based on the wavenumber integration method is first presented for the acoustic field in a Pekeris waveguide. The unconditional stability is achieved by normalizing both the up- and downgoing waves in water and the downgoing waves in the bottom appropriately. Hence, the present numerical solution entirely resolves the stability problem inherent in certain existing methods.

This paper then proposes a closed-form expression for the depth-dependent Green’s function for the Pekeris waveguide problem. It is also illustrated that as the density of the bottom goes to zero, the present analytical solution reduces to that in the ideal waveguide with a pressure-release sea surface and a pressure-release lower boundary; as the density of the bottom goes to infinity, the present analytical solution reduces to that in an ideal waveguide with a pressure-release sea surface and a rigid bottom; and as the density and sound speed of the bottom are separately equal to those in water, the present analytical solution reduces to that in a halfspace. The analytical solution for the depth-dependent Green’s function in a Pekeris waveguide is also implemented in a numerical model, which can deal with the Pekeris waveguide problem with either a point source in cylindrical geometry or a line source in plane geometry.

The wavenumber integration method is well-suited for the problem of sound propagation in shallow water at low frequencies. The present model, which uses the proposed exact solution for the depth-dependent Green’s function, is applied to several numerical examples. Numerical results indicate that the present model can provide accurate field results for general Pekeris problems. However, in the special case where a mode lies very close to the branch cut, KRAKEN might fail to provide accurate field results due to the neglect of the branch line integral. By introducing an artificial pressure-release lower boundary and using the Galerkin method, DGMCM (and COUPLE) can also provide accurate field results, which are in excellent agreement with those by the present model. For a single-frequency calculation, the probability of the occurrence of a mode lying near the branch cut is not great. For broadband calculations, however, the probability is high, as is illustrated in example 3 in this paper. Another scenario with a high probability encountering this phenomenon for single-frequency problems is when the bathymetry varies with range. The coupled-mode models COUPLE and DGMCM can handle this kind of range-dependent problem. However, this is achieved at the cost of having to involve much more normal modes than necessary due to the introduction of an artificial pressure-release lower boundary. We are interested in extending the wavenumber integration method to deal with range-dependent problems, and the present work provides a solid foundation for this research.

In conclusion, since no approximations have been introduced, the present model, which involves an analytical solution for the depth-dependent Green’s function, can provide exact field results and hence serve as a benchmark model for the acoustic field excited by either a point source or a line source in a Pekeris waveguide. Minor accuracy, which is generally negligible, might be sacrificed only in evaluating the wavenumber integral in the inverse Hankel transform.

Reference
1Pekeris C L1948Geol. Soc. Am. Mem.271
2Zhang Z YTindle C T1993J. Acoust. Soc. Am.93205
3Fawcett J A2003J. Acoust. Soc. Am.113194
4Buckingham M JGiddens E M2006J. Acoust. Soc. Am.119123
5Jensen F BKuperman W APorter M BSchmidt H2011Computational Ocean Acoustics2nd edn.New York: Springer10.1007/978-1-4419-8678-8
6Westwood E KKoch R A 1999 J. Acoust. Soc. Am. 106 2513
7Stickler D C 1975 J. Acoust. Soc. Am. 57 856
8Bartberger C L 1977 J. Acoust. Soc. Am. 61 1643
9Bucker H P 1979 J. Acoust. Soc. Am. 65 906
10Evans R B 1983 J. Acoust. Soc. Am. 74 188
11Luo W Y 2012 Sci. China-G: Phys. Mech. Astron. 55 572
12DiNapoli F RDeavenport R L 1980 J. Acoust. Soc. Am. 67 92
13Schmidt HJensen F B 1985 J. Acoust. Soc. Am. 77 813
14Jensen F BKuperman W APorter M BSchmidt H2000Computational Ocean AcousticsNew YorkAmerican Institute of PhysicsISBN: 1-56396-209-8
15Porter M B2001The KRAKEN normal mode program: Technical reportSACLANT Undersea Research Centre
16Evans R B 1986 J. Acoust. Soc. Am. 80 1414
17Luo W Y 2013 Chin. Phys. 22 054301