Biomedical ultrasound is one of the most active fields in modern ultrasonic technology, with ultrasonic diagnosis and treatment now widespread in biomedicine. The main application of biomedical ultrasound in clinical diagnosis is ultrasonic imaging such as B-ultrasound and D-ultrasound. Clinical treatment applications are mainly limited to ultrasonic lithotripsy and high intensity focused ultrasound based on cavitation and heat effects.^[1] High intensity focused ultrasound can make a focal area of tissue produce relatively large vibrations which are able to break up stones,^[2,3] and it is also an important medical technology in modern cancer treatment. The treatment principle of this technique is to achieve high sound intensity (10³ W/cm²–10⁴ W/cm²) by focusing sound energy generated by a large ultrasonic focusing transducer to achieve a high temperature (above 65 °C) in a focal area in a short period of time, causing tumor tissue to undergo thermal coagulation necrosis thus killing cancerous cells.^[4,5] High frequency ultrasound has better directivity and most of the sound energy can be focused on a target area without affecting surrounding tissues by accurate control of the ultrasonic focus, therefore it can realize noninvasive treatment.^[6,7] In practical applications, a sound wave generated by the transducer will pass through multiple biological media before reaching tumor tissue, and it is difficult to avoid reflection and scattering of sound energy because of the mismatch of acoustic impedance between different media, thus affecting the sound field of the target area, and distorting the sound field accordingly. Particularly in the treatment of liver cancer, the presence of the ribs can greatly influence the sound and temperature field, and ultimately affect the efficacy of the treatment. In early clinical treatments, surgical removal of ribs was often used to prevent reflections of ultrasound energy from affecting the stability of the sound field. Consequently, effective prediction of the distribution of the sound and temperature fields behind the ribs becomes very necessary in order to realize noninvasive treatment. Kamakura et al. used an ellipsoidal coordinate system to develop the spheroidal beam equation (SBE) based on the Westervelt equation.^[8] The SBE includes nonlinearity, diffraction, and absorption effects, and can be used to predict the sound field of a transducer with a wide aperture angle.^[8,9] Li et al. used the implicit-prediction correction method to calculate the influence of the ribs on a sound field under a cylindrical coordinate system using the Khokhlov–Zabolotskaya–Kuznetsov (KZK) equation^[10] while Liu et al. studied its temperature field.^[11] Lin et al. simulated and obtained the sound field of tissues behind ribs by focusing a transducer with a wide aperture angle under a three-dimensional ellipsoidal coordinate system using the SBE model.^[12] Fan et al. calculated the nonlinear sound field of a strong focusing transducer with a wide aperture angle using the SBE model,^[13,14] while Qian et al. investigated the influence of sound source parameters and material characteristics on the nonlinear effect of a concave spherical self-focusing sound field using the SBE model.^[15]

Previous articles generally analyze the sound field of a focusing transducer with a small aperture angle.^[8–10] Liu et al. studied the temperature field caused by weakly focused ultrasound^[11] and Lin et al. simulated and obtained the sound field of tissues behind ribs by focusing a transducer with a wide aperture angle.^[12] However, the innovative point of this paper is that we analyze the temperature field of a focusing transducer with a wide aperture angle on biological tissue containing ribs using the SBE model. In the paper, we first used the SBE to calculate the sound field produced by a focusing transducer with a wide aperture angle to obtain heat deposition, and then solved the Pennes bioheat equation to obtain the resulting temperature field in a biological tissue with ribs and study the effects of rib parameters on the temperature field.

The KZK equation is only suitable for a transducer with a half-aperture angle less than 16.6° due to the use of the parabolic or paraxial approximation, and the SBE equation can be used for a transducer with a wide half-aperture angle. A focusing transducer with a wide aperture angle is a spherical-shell focusing transducer with a spherical half-angle greater than 16.6°.^[16] Because such a wide angle focusing transducer has a larger radiating area, stronger focusing effect, smaller focal area radius and better penetrability than that of a small angle focusing transducer, a greater temperature rise can be generated within a tumor while reducing damage to other normal tissues.^[17]

Figure 1(a) shows a schematic diagram of the ellipsoidal coordinate system where a is the geometric radius of the radiating surface of the focusing transducer, α is the half-angle of the transducer, and 2b is the distance between two focal points of the ellipsoidal coordinate system. The horizontal axis represents the z axis as the σ direction, and the vertical axis represents the x–y plane. σ, η, and φ are the three coordinates of the ellipsoidal coordinate system, and σ = z = 0 is the geometric focal point.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. The ellipsoidal coordinate system and the division of the sound field, panel (a) is the schematic diagram of the ellipsoidal coordinate system, panel (b) shows the spherical wave area and a planar wave area.

As in Fig. 1(b), Kamakura et al. divided the paraxial sound field of a focusing transducer into a spherical wave area and a planar wave area.^[8] In this model, the cut-off point between the two areas is σ₀.^[18,19] The area less than σ₀ is the spherical wave area, which is close to the surface of the focusing transducer and forms a mainly spherical wave. The area larger than σ₀ is the planar wave area and this area is close to the focal point of the focusing transducer such that the planar wave is dominant.

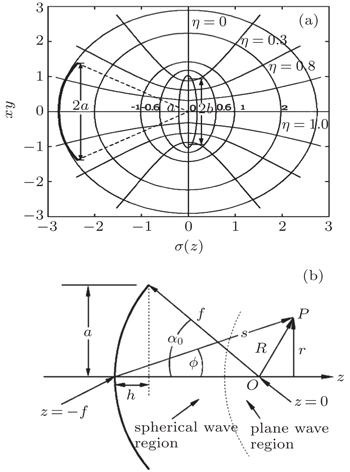
We calculated the sound field under the ellipsoidal coordinate system, and established the conversion relationship between the three coordinates (σ, η, ϕ) of the ellipsoidal coordinate system and the three coordinates (x, y, z) of the rectangular coordinate system:^[12]

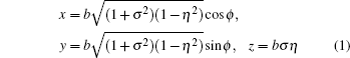
The Westervelt equation can be written as follows:^[16]

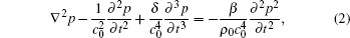
In the spherical wave area, the retarded time pertinent to the spherical wave is introduced:

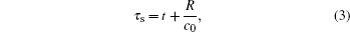
In the planar wave area, the retarded time pertinent to the planar wave is introduced:

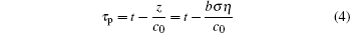
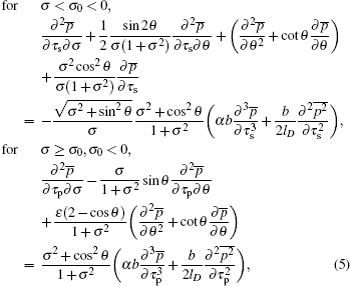
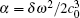
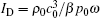
Consolidating Eq. (5) into an equation:

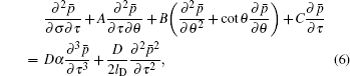
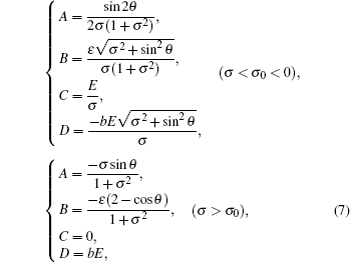
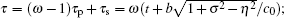
The normalized sound pressure is represented as the following Fourier series expansion:

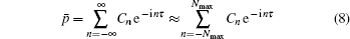
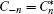
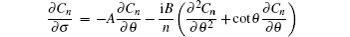
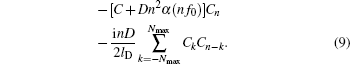
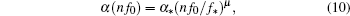
The heat deposition can be expressed as:

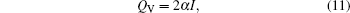
The Pennes bioheat equation^[20] can be written as:

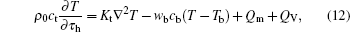
Because we study biological tissues in vitro, no heat flow from blood circulation exists, so that w_b can be neglected, Q_m can also be neglected in dead tissues. So the Pennes equation can be written as:

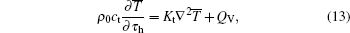
In the oblate spheroidal coordinate system, the Laplace operator

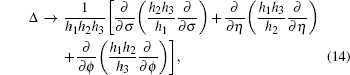
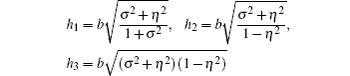
By substituting Eq. (14) into Eq. (13), we can obtain:

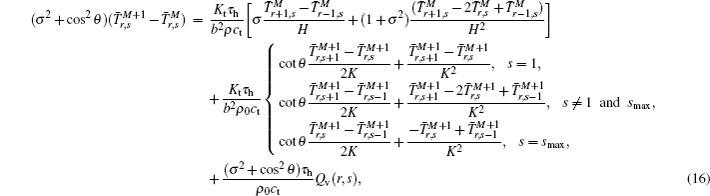
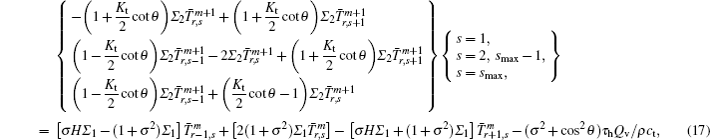
The matrix chase-after method (Thomas algorithm) is used to solve Eq. (17) and the distribution of the temperature rise in biological tissue can be obtained.^[22]

(i) In this paper, Tables 1 and 2 show the parameters of relevant biological tissues used in the simulation.

Table 1.

Table 1.

Table 1. Sound field parameters.[22] . Medium ρ0/kg·m−3 c0/m·s−1 α0/Np·m−1 MHz−1 β0 Water 1000 1500 0.0253 3.50 Fat 910 1430 9 10.5 Rib 1450 2350 90 Liver 1050 1596 4.5 6.00

Table 1. Sound field parameters.[22] .

Table 2.

Table 2.

Table 2. Temperature field parameters.[22] . Medium ct/J·K−1·kg−1 kt/W·m−1·K−1 Water 4180 0.50 Fat 3700 0.50 Rib 2000 0.43 Liver 3700 0.50

Table 2. Temperature field parameters.[22] .

(ii) Temperature rise in biological tissue without ribs

In order to guarantee the correctness of the simulation model, we should first compare the simulation results with actual values reported in the literature.^[22]

Figure 2 shows the axial temperature rise in tissue without ribs when the radius of the focusing transducer is 10 mm, the geometric focal length is 32 mm and the frequency is 1 MHz, the initial sound pressure is 380 kPa and radiation time is 10 s. The locations of fat and liver are shown in Fig. 2. The tissue layers comprise a fat layer of 15-mm thickness, followed by the liver. The maximum temperature rise is approximately 42 °C (the starting temperature of the tissue is 0 °C). Compared with the result in Ref. [22], where the maximum temperature rise is approximately 43 °C after 10 s, the simulation results of the two models are basically identical, which validates our numerical algorithm.

Fig. 2.

	Figure Option ViewDownloadNew Window
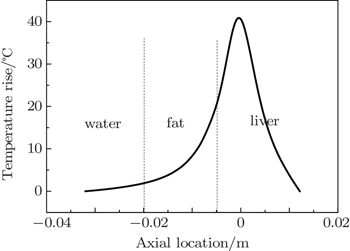	Fig. 2. The axial temperature rise in tissue without ribs when the radius of the focusing transducer is 10 mm.

Figure 3 shows the axial temperature rise of tissue without ribs when the radius of the focusing transducer is 50 mm, the geometric focal length is 100 mm and the frequency is 1 MHz, the initial sound pressure is 150 kPa, and the radiation time is 100 s. The locations of fat, liver, and water are shown in Fig. 3. The tissue layers comprise a fat layer of 50-mm thickness, followed by the liver. From Fig. 3, the maximum temperature rise is 53 °C in the liver and less in fat.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. The axial temperature rise in tissue without ribs when the radius of the focusing transducer is 50 mm.

Figure 4 shows the radial temperature rise of the same case as in Fig. 3 where the temperature rises are in fat at an axial location of z = −17 mm, liver-1 at an axial location of z = −6.7 mm, and liver-2 at an axial location of z = 0.3 mm. From Fig. 4, the temperature rise in fat becomes smaller and the range of the temperature rise is larger, while the maximum temperature rise is seen in the liver when it is close to the geometric focus where the range of the temperature rise is very small, which indicates that the closer a tissue is to the geometric focus, the better the focusing effect, and the greater the temperature rise.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. The radial temperature rise in tissue without ribs at different axial locations.

(iii) Temperature rise of a biological tissue with two ribs located symmetrically on either side of the axis

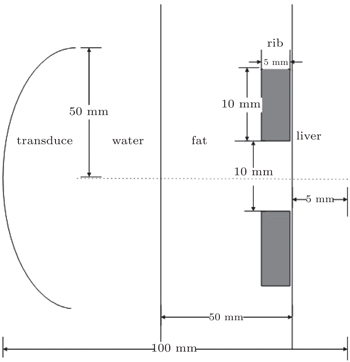
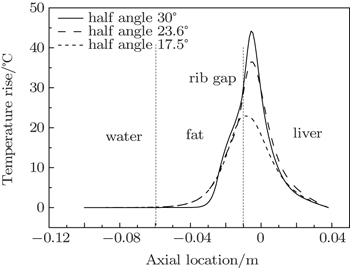
Next, we investigated the influences of the initial sound pressure, frequency, half-angle of the transducer, gap width and the location of ribs on the temperature rise of biological tissues under the condition that the half-angle is 17.5°, 23.6°, and 30° respectively. The locations of fat, liver and two ribs are shown in Fig. 5. The tissue layers comprise a fat layer of 50-mm thickness, followed by the liver, and the ribs are embedded in the fat layer. The ribs can be seen as an acoustic rigid boundary and have total reflection to ultrasonic wave.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. The tissue with two ribs located symmetrically on both sides of the axis.

Figure 6 shows the axial temperature rise at different half-angles when the radius of the focusing transducer is 50 mm, geometric focal length is 100 mm, frequency is 1 MHz, initial sound pressure is 100, 150, or 200 kPa, rib width is 10 mm, rib thickness is 5 mm and rib gap width is 10 mm, and radiation time is 100 s. From Fig. 6, it is evident that sound energy can pass through the rib gap, the focal point is in the liver, and the maximum temperature rise is slightly smaller than that without ribs. Fat also undergoes a smaller temperature rise due to the obstruction of the ribs. As the initial sound pressure increases, the sound energy at the focal point increases which leads to an increase in the temperature rise. As the transducer half-angle increases, the sound energy that can pass through the rib gap increases, so the maximum temperature rise increases and the location moves backward.

Fig. 6.

	Figure Option ViewDownloadNew Window
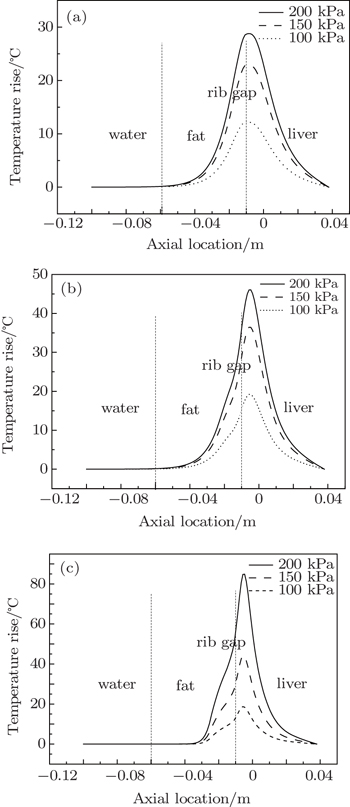	Fig. 6. The axial temperature rise in tissue with two ribs at different sound pressures under the condition that the half-angle is (a) 17.5°, (b) 23.6°, and (c) 30° respectively.

Figure 7 shows the radial temperature rise of the same case as shown in Fig. 6 where the initial sound pressure is 150 kPa, and the temperature rise is calculated at an axial location of fat z = −23mm, an axial location of liver-1 z = −8.8mm and an axial location of liver-2 z = 0.3 mm. From Fig. 7, it can be seen that the sound energy can pass through the rib gap to reach the liver, so the maximum temperature rise occurs in the liver. However, as a result of the obstruction of the ribs, the maximum temperature rise is located in front of the geometric focus, further forward than without ribs.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. The radial temperature rise in tissue with two ribs at different axial locations under the condition that the half-angle is 30°.

Figure 8 shows the axial temperature rise at different half-angles when the initial sound pressure is 150 kPa, the frequency is 1, 1.2, or 1.5 MHz, and other parameters are the same as those in Fig. 6. Figure 8 shows that as the frequency increases, the diffraction effect of the sound field decreases, so the focusing effect is enhanced, but part of the energy cannot pass through the ribs while the sound absorption coefficient increases since the sound absorption coefficient is in proportion to the power of the frequency (μ = 1.1–1.3). Taking into account the above two factors, no change in the temperature rise of the liver with frequency is evident. The maximum temperature rise of fat increases because the reflective energy induced by the ribs increases when the diffraction effect of the sound field decreases, and the focusing effect is enhanced as the frequency increases, and moves forward slightly.

Fig. 8.

	Figure Option ViewDownloadNew Window
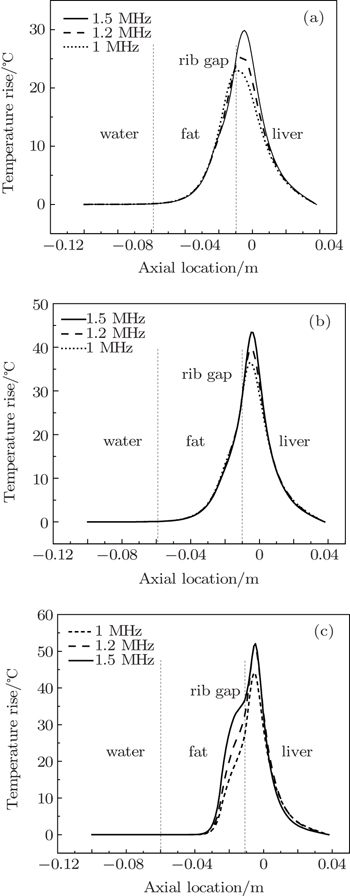	Fig. 8. The axial temperature rise in tissue with two ribs at different frequencies under the condition that the half-angle is (a) 17.5°, (b) 23.6°, and (c) 30° respectively.

Figure 9 shows the axial temperature rise when the initial sound pressure is 150 kPa, the transducer half-angle is 17.5°, 23.6° or 30°, and other parameters are the same as those in Fig. 6. As shown in Fig. 9, as the transducer half-angle increases, the focusing effect is enhanced, the sound energy that passes through the rib gap increases, the maximum temperature rise increases and the location moves backward slightly.

Fig. 9.

	Figure Option ViewDownloadNew Window
	Fig. 9. The axial temperature rise in tissue with two ribs at different half-angles.

Figure 10 shows the axial temperature rise at different half-angles when the initial sound pressure is 150 kPa, the gap width of the ribs is 10, 12 or 15 mm, and other parameters are the same as those in Fig. 6. From Fig. 10, as the gap width of the ribs narrows, the sound energy that can pass through the rib gap decreases, and the maximum temperature rise decreases. Because the obstruction of the ribs increases with reducing gap width, the location of the maximum temperature rise moves forward.

Fig. 10.

	Figure Option ViewDownloadNew Window
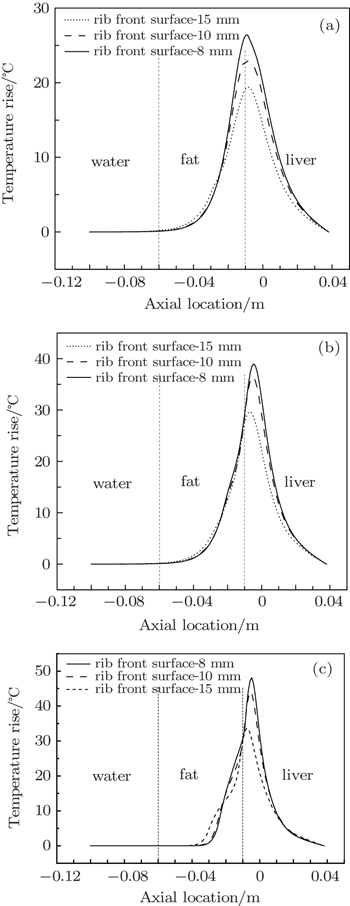
	Fig. 10. The axial temperature rise in tissue with two ribs at different rib gap widths under the condition that the half-angle is (a) 17.5°, (b) 23.6°, and (c) 30° respectively.

Figure 11 shows the axial temperature rise at different half-angles when the initial sound pressure is 150 kPa, the distance between the front surface of the rib gap and the geometric focus is 8, 10 or 15 mm, and other parameters are the same as those in Fig. 6. From Fig. 11, as the ribs are closer to the transducer surface, the sound energy that passes through the gap between the ribs at the focus decreases, the maximum temperature rise decreases, and the location of the maximum temperature rise is forward with the ribs.

Fig. 11.

	Figure Option ViewDownloadNew Window
	Fig. 11. The axial temperature rise in tissue with ribs at different distances between the front surface of the rib gap and the geometric focus under the condition that the half-angle is (a) 17.5°, (b) 23.6°, and (c) 30° respectively.

From the results of our simulation, it can be seen that the influence of ribs on the temperature field in biological tissue is very obvious. The location and the gap width of the ribs both have a great influence on the temperature rise of biological tissue. As two ribs are distributed on either side of the axis, a sound wave can pass through the rib gap, so there is a relatively high temperature rise in the liver. As the gap width between the ribs increases, the sound energy that passes through increases, so the temperature rise of the liver also increases. As the ribs are closer to the focusing transducer, the focusing effect decreases and less sound energy passes through the rib gap, so the temperature rise of the liver decreases. Consequently if we want to achieve a higher temperature rise in the liver, in addition to increasing the initial sound pressure or the half-angle of the focusing transducer, we can also increase the distance between the transducer and the ribs. This work can provide guidance for the practical treatment of liver cancer.