Much effort has been conducted recently to describe the characteristics of different laser beams, like the M²-factor, power fraction ‘PIB’, kurtosis factors, etc. As is well known, the beam propagation factor is a useful parameter for describing laser beam quality^[1] which is based on the second-order moment, while the fourth and second-order intensity moments have been used to define the so-called kurtosis parameter K, which is a measure of symmetry and sharpness (or degree of flatness) for the intensity distribution of a laser beam.^[2] The intensity profile of any laser beam is classified as leptokurtic, mesokurtic or platykurtic distributions according to the kurtosis value K being higher, equal or less than 3, which is the kurtosis value of the fundamental Gaussian beam for the one-dimensional case.^[3]

On the other hand, the kurtosis parameters of various laser beams, except a few types, Gaussian and Hermite-Gaussian beams, change their magnitudes during the beam propagation through an unapertured paraxial optical ABCD system.^[4] Many studies have been provided about the kurtosis parameter characteristics of different laser beams, such as flattened Gaussian beams, Bessel-modulated Gaussian beams, elegant Hermite–Gaussian, elegant Cartesian Laguerre–Hermite–Gaussian and Laguerre–Gaussian beams, Hermite–cosh–Gaussian beams, etc., propagating through ABCD optical systems.^[4–13]

The aim of the present work is to study the propagation of the kurtosis parameter of a hypergeometric-Gaussian type-II (HyGG-II) beam. The rest of this paper is organized as follows: in Section 2, we give the theory of the propagating HyGG-II beams in a paraxial optical ABCD system, and in Section 3, we present the theoretical expressions of the kurtosis parameters of the considered beam family. In order to illustrate the obtained results, we present some numerical simulations and discussions in Section 4. Finally, we draw some conclusions in Section 5.

In a polar coordinate system (r₀, θ₀), the electric field distribution of a HyGG-II beam at the plane z = 0 is described as^[14]

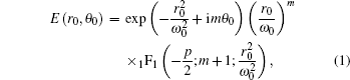
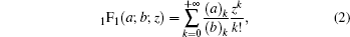
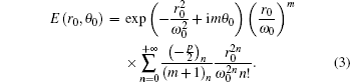
Figure 1 shows the plots of the normalized distribution of intensity of a HyGG-II beam based on Eq. (1) for different values of m. It can be easily seen that the increasing value of m makes the profile shape of the intensity of the HyGG-II beam far hollower.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Normalized intensity distributions of HyGG-II beam in the 3D direction at the z = 0 plane, ω0 = 1 mm and p = 1.2 for m = 1 (a), 2 (b), and 3 (c).

The propagation of a general beam through an optical paraxial ABCD system is described by Huygens’s integral in the Kirchhoff–Fresnel approximation

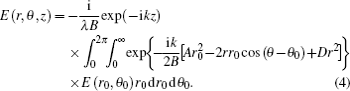
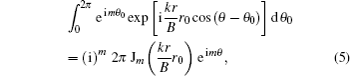
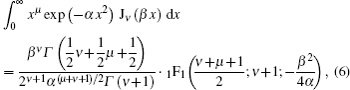
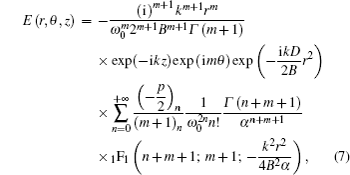
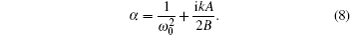
The kurtosis parameter of rotationally symmetric laser beams in the cylindrical coordinate system can be defined as^[4,11]

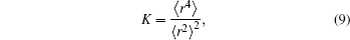
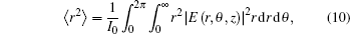
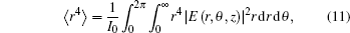
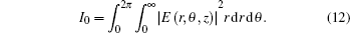
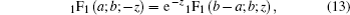
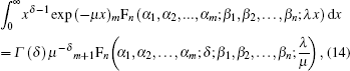
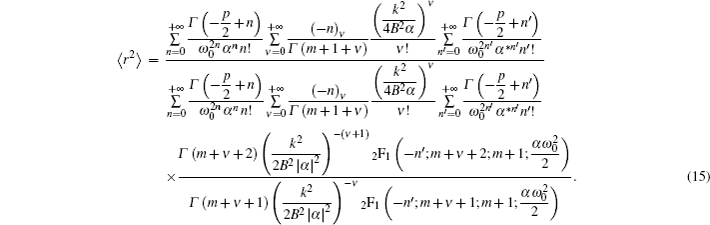
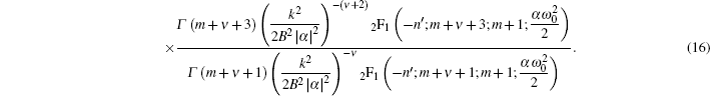
Three interesting special cases of Eq. (17) are as follows.

Case a For the case of p = m = 0, equation (17) reduces to K = 2, which is the kurtosis parameter value of the fundamental Gaussian beam in cylindrical coordinate domains.^[11–13]

Case b For the case of p = −m, equation (17) reduces to

Case c For p ≥ 0 even integer number, we find the K parameter of elegant Laguerre–Gaussian beams propagating through a paraxial ABCD optical system.^[14]

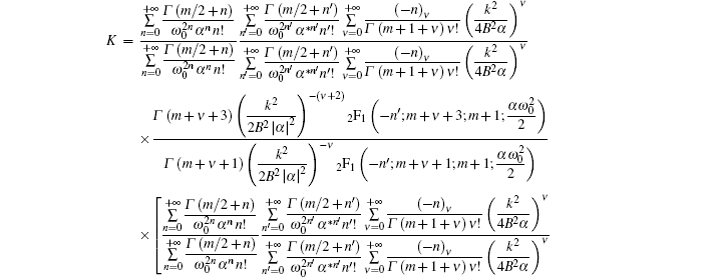
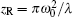
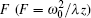
In this section, the matrix elements are chosen to be A = 1, B = z, C = 0, and D = 1. The other parameters are λ = 0.6328 μm, ω = 2 mm, and the Rayleigh range . A number of numerical simulations are performed by using the obtained analytical expressions which are given in Figs. 2–6, where the propagation of a HyGG-II beam through free space is represented for different values of propagation distance. The propagation of the kurtosis parameter of the HyGG-II beam is plotted against Fresnel number . The hollowness parameter p and the beam order m are chosen as calculation parameters. According to the analytical formula derived in Section 2 (Eq. (7), we draw Figs. 2 and 3. Figure 2 shows the intensity distributions of the HyGG-II beam propagating in free space for various values of the hollowness parameter p and distance of propagation z.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Intensity distributions of the HyGG-II beam each as a function of r with λ = 0.6328 μm, m = 1, ω0 = 2 mm for z = zR (a), 4zR (b), and 6zR (c).

Fig. 3.

	Figure Option ViewDownloadNew Window
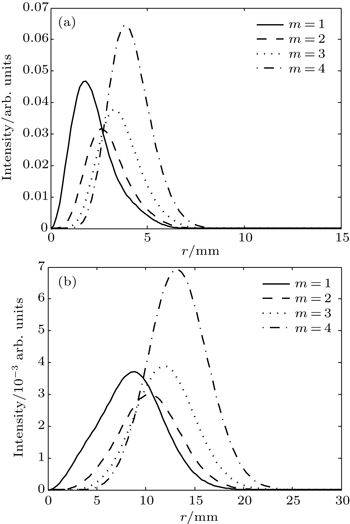	Fig. 3. Intensity distributions of the HyGG-II beam each as a function of r with λ = 0.6328 μm, p = 1.2, ω0 = 2 mm for z = zR (a) and 4zR (b).

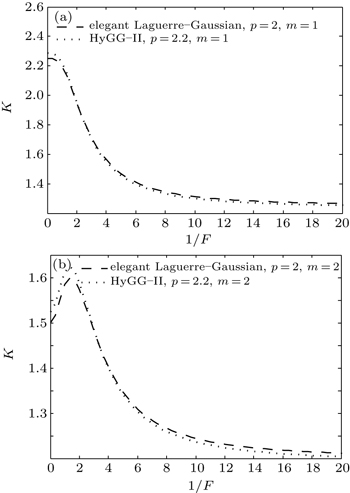
From Fig. 2, we can see that the intensity distributions of the HyGG-II beam decrease with an increase in parameter p and distance z. The effect of the beam order on the intensity distribution of HyGG-II beams is illustrated in Fig. 3. Also, it is clear from both Fig. 2 and Fig. 3 that the central dark region is widened as m, p, and distance z values increase.

Figure 4 originates from the implementation of Eq. (17) for even integer number p, which represents variation of the kurtosis parameter K of elegant Laguerre–Gaussian beams with Fresnel number F. This result is the same as that of Ref. [4]. It is clear from this figure that the parameter K of elegant Laguerre–Gaussian beams decreases with an increase in both m and p parameters and remains unchanged with the increase of the inverse of F.

Fig. 4.

	Figure Option ViewDownloadNew Window
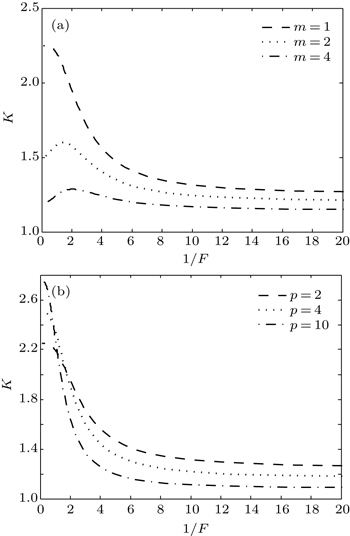	Fig. 4. Variations of kurtosis parameter K of an elegant Laguerre–Gaussian beam with Fresnel number F in the cases of p = 2 (a) and m = 1 (b).

The dependence of the kurtosis parameter K of an MQBG beam on generalized Fresnel number F are illustrated in Fig. 5 by using the analytical expression shown in Eq. (16) for different values of the beam order. Also, from this figure, it is clear that the values of the kurtosis factor of the MQBG beam decrease with the increase of the beam order m till a certain value of 1/F independent of m (for each m value), then, they increase. However, in the far field, the intensity profile of the MQBG beam remains unchanged whatever the value of 1/F is.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Variations of kurtosis parameter K of a MQBG beam with Fresnel number F for three different values of m.

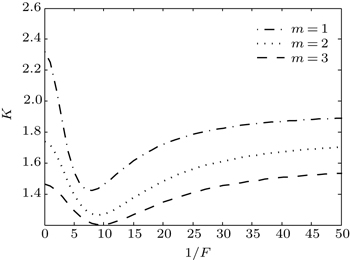
It can be seen from Fig. 6 that (see Eq. (17)) each parameter K reaches its maximum value, and then decreases with the increase of the inverse of F, and then approaches to an asymptotic value corresponding to the limiting value of K when 1/F (or z) tends to infinity because the intensity profile in the far field of HyGG-II beams is unchangeable. The asymptotic value depends on p and m values. For example, Fig. 6.

Variations of kurtosis parameter K of a HyGG-II beam with Fresnel number F in the cases: m = 1 (a) and 2 (b) for different p values; and p = 1.2 (c) for different m values.

the asymptotic values are 1.17 for p = 4.2 in Fig. 6(a) (m = 1), 1.15 in Fig. 6(b) (m = 2), 1.2 for p = 3.2 in Fig. 6(a) (m = 1), and 1.17 in Fig. 6(b) (m = 2), respectively. The maximum value of the kurtosis parameter K of the HyGG-II beam increases with the increase of the hollowness parameter p (Figs. 6(a) and 6(b)). This means that the distributions of the intensity of these beams are dispersed around the center at p = 1.2, then they are concentrated around the center with the increase of p. In the second phase, the kurtosis parameter K of the HyGG-II beams decreases with the augmentation of the beam order m, which can be explained by the fact that the dark area diameter of the HyGG-II beams becomes very large.

Finally, by using our main result in Eq. (17), we compare our obtained result of the variation of the kurtosis parameter of the HyGG-II beam with that of the elegant Laguerre–Gaussian beam. Figure 7 shows that the variation of the kurtosis parameter of the elegant Laguerre–Gaussian beam is weaker than that of the HyGG-II beam. So, the degree of flatness of the intensity distribution of the HyGG-II beam is more convenient for many applications of optical physics.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. Comparisons between the kurtosis parameter K value of the elegant Laguerre–Gaussian beam as a function of the Fresnel number F and that of the HyGG-II beam as a function of the Fresnel number F in the cases: m = 1 (a) and 2 (b).

From the previous figures, we can conclude that the values of the kurtosis factor of the HyGG-II beam and their subfamilies are always smaller than 3. Therefore, we can say that the HyGG-II beams are classified within the leptokurtic distribution.

In this paper, based on the propagation equation of the HyGG-II beam propagating through a paraxial ABCD optical system, the analytical expression for the kurtosis parameter of the HyGG-II beam is derived. The obtained results show that the kurtosis parameter of the HyGG-II beam changes with beam order m, and hollow parameter p. In addition, the K parameter of the fundamental Gaussian beam, the kurtosis of the superposition of two modified-Bessel beams and the kurtosis of the elegant Laguerre–Gaussian beam are obtained analytically as special cases and illustrated numerically.