Octave-spanning laser based frequency combs have increasing applications in many fields like frequency metrology^[1] and optical spectroscopy,^[2,3] benefiting from the direct output broad spectra from the oscillators.^[4,5] Currently, the most widely used technique to measure and control the CEO frequency (f_ceo) of an octave-spanning oscillator is the so-called self-referenced scheme,^[6–11] in which the supercontinuum generation and f–2 f interferometer are essential for the f_ceo detection. However, the apparatus employed in these two procedures are relatively complex and bulky in size, and the stability of the f_ceo signal is sensitive to the fiber coupling and the double-optical-path alignment of the f–2 f systems. Moreover, a considerable portion of the laser beam should be split off the main output to the interferometer to generate the f_ceo beat note, which inevitably decreases the output power available for the subsequent experiments.

In 2005, a novel CEO measurement technique based on the difference frequency generation (DFG) was proposed by Fuji et al.^[12,13] This scheme, which is termed the monolithic scheme or 0–f scheme, has a simple coaxial light configuration and has been demonstrated to possess relatively lower phase noise in comparison with the traditional self-reference method.^[13,14] Besides, beam splitting is not necessary here and there is almost no power loss in the process of f_ceo measurement. Nevertheless, the utilization of the monolithic CEO stabilization scheme is still limited to the oscillators with quasi-octave-spanning spectra^[15–18] so far, because both the high single-pulse energy and broad output spectrum of an oscillator are essential conditions to cause strong nonlinear processes for the f_ceo signal generation.^[19,20] This, on the other hand, indicates that the octave-spanning lasers, which have broader output spectra and thus potentially shorter pulse durations compared with quasi-octave-spanning lasers, would be more suitable to adopt the monolithic method for the CEO control.

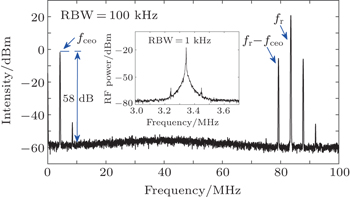
Up to now, there is no report about the CEO stabilized octave-spanning laser by use of the monolithic scheme. In this paper, we first experimentally demonstrate the octave-spanning laser based frequency comb by use of the monolithic CEO stabilization scheme. A wide spectrum ranging from 480 nm to 1050 nm was directly generated from an all-chirped mirror Ti:sapphire laser. With this monolithic method, the signal-to-noise ratio (SNR) of f_ceo of the octave-spanning laser was measured to be as high as 58 dB under a resolution of 100 kHz. This is, to the best of our knowledge, the highest f_ceo SNR among the existing octave-spanning laser based frequency combs. Using a phase-locking loop with a feedback bandwidth of 50 kHz, we realized an IPN (integrated from 1 Hz to 1 MHz) of 55 mrad for the locked CEO beat signal, equivalent to a timing jitter of 23 as at the central wavelength of 790 nm. The Allan deviation (1-s gate time) of the f_ceo is 2×10⁻¹⁷ to the optical carrier frequency. These good performances in phase noise and long-term stability derive from the high stability of our oscillator and the monolithic CEO detection method.

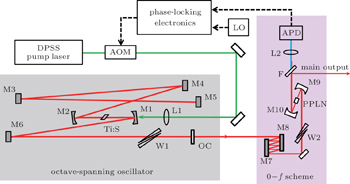
The octave-spanning frequency comb, as revealed in Fig. 1, is based on a home-made all-chirp-mirror Ti:sapphire laser with a repetition rate of 83 MHz. A 1.9-mm-thick Ti:sapphire crystal (α₅₃₂ = 7 cm⁻¹) is placed in the middle of two folding mirrors with 100-mm radii of curvature. All the intracavity mirrors (M1–M6) are broadband doubled-chirped mirror (DCM) pairs with high reflection from 580 nm to 1000 nm and group delay dispersion (GDD) from 600 nm to 980 nm, totally providing around −200-fs² GDD to compensate for the positive dispersion introduced by the gain crystal as well as air path. A pair of wedges (W1) at the Brewster angle is used to finely tune the intracavity dispersion.

Fig. 1.

Figure Option ViewDownloadNew Window

Fig. 1. Experimental setup of the octave-spanning frequency comb based on the monolithic carrier–envelope (0–f) scheme. AOM, acousto–optic modulator; L1, pump lens (f = 50 mm); L2, filter lens (silica-doped, f = 30 mm, cutoff frequency: 1000 nm); T:S: Ti:sapphire crystal (1.9-mm-thick, α532 = 7 cm−1); M1–M6 and M7–M8, double-chirped mirror pairs (HR: 580 nm–1000 nm, GDD: 600 nm–980 nm)); M9–M10: silver mirrors (ROC = 30 mm); OC, fused-silica output coupler (3-mm-thick); W1–W2, fused-silica wedges; PPLN: periodically poled lithium niobate crystal (3-mm-thick, Poling period: 17.84 μm); F: broadband filter (HR: 600 nm–980 nm); APD: avalanche photodiode; LO: local crystal oscillator.

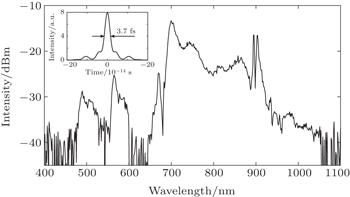
After carefully adjusting the alignment of the oscillator, more than 310-mW stable Kerr-lens mode-locked (KLM) pulses could be obtained under 4.5-W pump power from the diode-pumped solid-state laser. Figure 2 shows the typical output spectrum of more than one octave extending from 480 nm to 1050 nm, corresponding to a Fourier transformation limit of 3.7 fs, as shown in the inset of Fig. 2. One can notice that there are two obvious peaks at 490 nm and 564 nm isolated from the continuous spectrum. These spectral modulations, including the peaks and dips, are mainly introduced by the coherent superposition between the intracavity soliton and the dispersive wave,^[21] which derives from the strong nonlinearity effect inside the KLM oscillator.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Typical output spectrum of the octave-spanning oscillator, covering the wavelengths spanning from 480 nm to 1050 nm.

After dispersion pre-compensation by a DCM pair (M7, M8) and wedges (W2) outside the cavity, the output pulses were tightly focused into a 3-mm periodically poled lithium niobate (PPLN) crystal. The poling period of this crystal (17.84 μm) is specifically designed in terms of the oscillator’s spectrum distribution. New spectral components around 1.6 μm were generated by both the self-phase modulation (SPM) and DFG inside the PPLN crystal at the same time. It is worth noting that the frequency difference between the produced components from the SPM and the ones from the DFG is exactly the f_ceo value of the octave-spanning laser.^[12] In the experiment, we employed a long-pass filter lens (L2) to filter out the components around 1.6 μm to realize this collinear frequency-beat process. Ultimately, the free running f_ceo beat signal was directly detected by an infrared InGaAs avalanche photodiode (APD, New Focus 1181-FS).

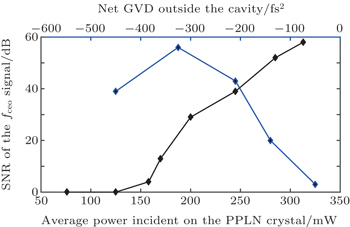
We experimentally found the f_ceo signal in the monolithic theme was sensitive to the output power of the oscillator and the dispersion compensation outside the laser cavity. In order to obtain a strong beat note, we explored the SNR of the f_ceo as functions of average power incident on the PPLN crystal (under −270-fs² net GDD provided outside the cavity) and the net GDD provided outside the cavity (under 313-mW power incident on the PPLN crystal), as shown in Fig. 3. We can see that the f_ceo almost increases linearly with the incident power above the threshold. This trend, however, could not persist in our experiments since multi-pulse phenomena in our Ti:sapphire oscillator would appear when the oscillator’s output power was more than 320 mW. The optimal outside GDD compensation for the f_ceo was found to be about −320 fs², for providing a pre-compensation to the dispersion caused by the PPLN crystal and ensuring the precision synchronization between the two beat beams.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. The SNR of the fceo signal as functions of average power incident on the PPLN crystal (black line, under −270-fs2 net GDD provided outside the cavity) and net GDD provided outside the cavity (blue line, under 313-mW power incident on the PPLN crystal).

Figure 4 shows the f_ceo-optimized radio-frequency (RF) spectrum measured with an RF analyzer (FSW 26, Rohde & Schwarz Inc.). A strong f_ceo SNR of 58 dB is obtained under a resolution of 100 kHz. Its detail is revealed in the inset of Fig. 4. Such a high f_ceo intensity is of great significance in the suppression of the circuit introduced noise and in the demand reduction of the circuit’s signal-capture ability. The repetition rate (f_r), the corresponding double sidebands (f_r− f_ceo and f_r+ f_ceo) and even the second harmonic of the f_ceo can be seen clearly with a wide-span measurement of 100 MHz.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Radio-frequency (RF) spectrum of the free running fceo (RBW = 100 kHz and span = 100 MHz) directly measured by the APD. fr denotes repetition rate and fceo denotes the CEO frequency. The inset: the magnified frequency peak of fceo (RBW = 1 kHz and span = 700 kHz).

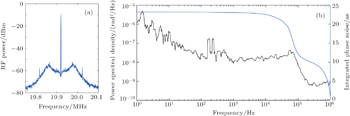
The phase error signal detected by the APD was then feedback to change the power of the pump light via an acoustic optical modulator (AOM). A local quartz crystal oscillator was employed as an external crystal oscillator. The in-loop noise performance of the stabilized f_ceo beat signal is directly measured and revealed in Fig. 5. We can see that the linewidth of the f_ceo signal is dramatically narrowed compared to the previous free-running case (see the inset in Fig. 4), which illustrates that a tight phase-lock has been achieved. Although the AOM is experimentally confirmed to possess a broad modulation bandwidth of more than 1 MHz, the whole feedback bandwidth of the phase-locking systems is less than 100 kHz, which is mainly limited by the bandwidth of the phase locked loop and the upper-level life of the Ti:sapphire crystal.^[22] This conclusion is also confirmed by the two bumps on the noise pedestal in Fig. 5(a), which are ∼ 50 kHz beside the coherent peak.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Noise properties of the locked fceo beat signal measured from the in-loop APD. (a) The detail of the fceo signal (RBW = 1 kHz) observed by an RF analyzers. (b) Power spectral density (PSD) and integrated phase noise (IPN) of the fceo frequency ranging from 1 Hz to 1 MHz.

For a quantitative analysis of the noise property, the power spectral density (PSD) was measured and displayed in Fig. 5(b). The corresponding integrated phase noise (IPN) from 1 Hz to 1 MHz is calculated to be 55 mrad, equivalent to a timing jitter of 23 as at the carrier wavelength of 790 nm. Note that the high-frequency phase noise, especially frequencies higher than the feedback bandwidth of the servo system, has a considerable contribution to the residual phase noise. Even so, our residual phase noise with the same integrated range is still a three-fold improvement compared with the result in Ref. [8], in which the f–2 f scheme was chosen as the f_ceo measurement method for the octave-spanning oscillator.

Long-term locking of the f_ceo signal could be achieved due to the high stability of the monolithic CEO stabilization scheme. The locking result around 90 minutes is shown in Fig. 6. The corresponding Allan deviation is calculated to be 4×10⁻¹⁰ (1-s gate time) for the 20 MHz, which only contributes about 2×10⁻¹⁷ to the optical carrier frequency instability (f_c ≈ 380 THz). We believe the IPN and the long-term stability would be both further improved if the locking circuits and the measuring apparatus are all referenced to a stable atomic clock.^[23]

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. The frequency deviation of fceo recorded around 90 minutes. Corresponding Allan deviation for 1-s gate time is 4×10−10.

We first utilized the monolithic CEO stabilization scheme to measure and control the f_ceo beat note of an octave-spanning oscillator. After a series of improvements, the CEO beat note with a 58-dB SNR (RBW = 100 kHz) was achieved, which is the highest f_ceo SNR among the octave-spanning laser based frequency combs to date. When locked to an extra crystal oscillator, the phase error signal of f_ceo was obviously suppressed within the feedback bandwidth of the phase-locking loop. We realized the residual phase noise was only 55 mrad (integrated from 1 Hz to 1 MHz), equivalent to a timing jitter of 23 as at the center wavelength of 790 nm. This little jitter between the carrier and envelope phase will have a directly positive impact on the consequent applications, such as the multispectral coherent synthesis and the intense field control of the attosecond pulse generation.