Cavity quantum electrodynamics (QED) has aroused increasing interest since the Purcell effect was proposed in 1946^[1] and testified in a laboratory in 1947.^[2] A typical cavity QED system consists of a cavity photon subsystem and an atomic subsystem. A high-finesse cavity confines light into a small volume and holds photons over a long time before dissipation because of its good insulation against the environment. Such an artificial confined structure offers an appropriate stage on which the atom system as a sensitive needle may detect weak variation from the background and show a series of new and interesting effects. By means of these effects we may understand the fundamental problems of light-matter interaction and the basic properties of the changed vacuum field. A variety of theoretical and experimental subjects utilizing the cavity QED system have been explored over the past years, including enhanced or weakened quantum interference effects,^[3–5] a change of spontaneous emission,^[6–9] electromagnetically induced transparency,^[10–12] population dynamics or quantum state manipulation.^[13–16]

Among all the above topics, the dynamics control of quantum states is of crucial importance for practical applications in quantum physics. In the past few years various measures have been adopted to control the dynamics of quantum states or population trapping.^[17–27] For instance, in a two-coupled atom–cavity system, a wide variety of time-evolution behaviors have been shown by modulating the coupling strength and the hopping strength.^[17] For two Λ-type atoms inside a cavity, a nonadiabatic scheme to accelerate the population transfer and the creation of maximal entanglement between two atoms has been proposed in line with Berry’s transitionless quantum driving approach.^[24] Moreover, population trapping in the excited state arises if a two-level atom is embedded in a dissipative cavity, which is coupled to a bosonic environment.^[25] Besides, a laser field is frequently used independently or jointly with a cavity field to manipulate population cooling or inversion^[28–34] and a radio-frequency field is also applied to fine structure systems.^[35] For a V-type three-level atom with two upper states close in energy levels, the usual way to control the dynamics of an atom is to use two different lasers with their wavelengths finely and appropriately tuned. Yet, using the combination of a microwave field with a much lower frequency together with a laser field can also be an alternative way to provide a feasible measure to control the interaction between an atom and a field. To our knowledge, such a scheme has not been studied. Therefore, in order to understand the properties of the single atom–cavity system more broadly and deeply, it is meaningful to study the dynamics of population for a V-type three-level atom–cavity coupling system driven by an external microwave field.

In this paper, we present a scheme of population transfer among different quantum states for a three-level V-type atom confined in a single-mode cavity. Meanwhile, as in an actual situation, a classical microwave field with a much lower frequency than a common laser field is added between the two upper levels of the atom (with two upper states close in energy level). Under the cooperative and competitive operation of the cavity field and the microwave field simultaneously, the system exhibits many freedoms to manipulate the interaction between the atom and cavity, the atom and classical field, including the coupling coefficient (g), the Rabi frequency (Ω_e) associated with the external field, the detuning (δ) between the atom and the external field, the detuning (Δ) between the atom and the cavity field, and initial conditions. The coupling coefficient g (g = D(ω_c/2ħɛ₀V)^1/2, where D is the atomic dipole moment, ω_c is the frequency of the cavity mode, ħ is the Planck constant, ɛ₀ is the vacuum permittivity, V is the cavity mode volume)^[36] reflects the strength of the atom–cavity interaction directly. 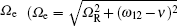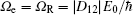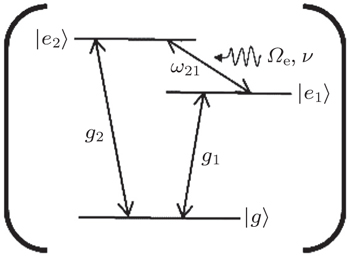On the other hand, Rabi frequency , in the case of resonance, we obtain , here D₁₂ is the dipole matrix element, E₀ is the amplitude of the external field, and ω₁₂ is the resonant frequency between the upper two atomic levels) reflects the strength of the external microwave field. In this paper, we will discuss the dynamics of a three-level V-type atom driven simultaneously by a cavity photon and microwave field by modulating two parameters g and Ω_e. A variety of dynamic evolution behaviors about the atom states and cavity photon states can be expected by modulating the two parameters.

The system considered is depicted in Fig. 1. It consists of a three-level V-type atom and a single-mode cavity whose dissipation is neglected. The two upper levels |e₁〉 and |e₂〉 are coupled to the lower level by the coupling constant g_i. The resonant frequency of the cavity mode is ω_c. The atomic transition |e₁〉 ↔ |e₂〉 is driven by a microwave classical field with Rabi frequency Ω_e. For convenience, we assume that the system temperature is 0 K, where the dephasing rate of the quantum states can be neglected.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Schematic diagram of a three-level V-type atom confined inside a single-mode cavity with coupling constant gi, atomic transition |e1〉 ↔ |e2〉 is driven by a microwave field with Rabi frequency Ωe and carrier frequency ν.

In the interaction picture, the Hamiltonian for the system can be described as

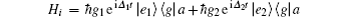
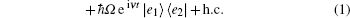
Here, a^† (a) is the creation (annihilation) operators of the cavity mode; |g〉 and |e_i〉 (i = 1, 2) are the ground and excited states of the atom; Δ₁ = ω_c − (ω₁ − ω_g) and Δ₂ = ω_c − (ω₂ − ω_g) are the detuning between the transition frequency of the two upper levels and the resonant frequency of the cavity mode; Ω_e denotes the Rabi frequency of the external driving field; ν is its carrier frequency.

The solution and discussion of the Hamiltonian are restricted to the subspace which contains only zero and one excitations. Thus, the state vector of the system at time t is

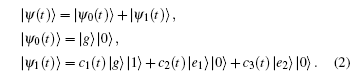
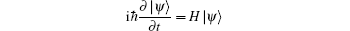
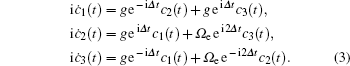
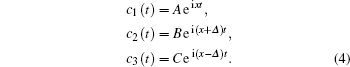
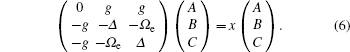
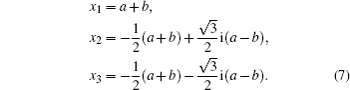
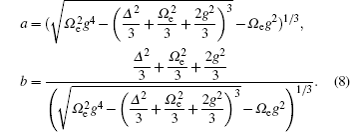
In our model, the detuning Δ is set to be 0.1. Therefore, three eigenvalues are only subjected to the influence from the coupling constant g and the Rabi frequency Ω_e. A close look at Eq. (7) and Eq. (8) shows that all eigenvalues are real numbers, which is consistent with the fact that the dissipation of the system is neglected.

Substitute three eigenvalues into Eq. (5), then we will obtain

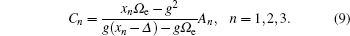
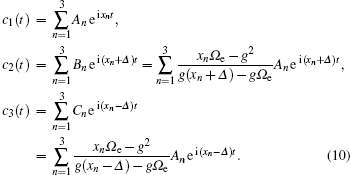
We now assume that the atom is initially prepared in the superposition state of the two upper levels with the same probability amplitude and the cavity is in a vacuum state and given as

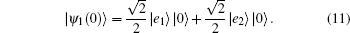
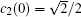
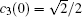
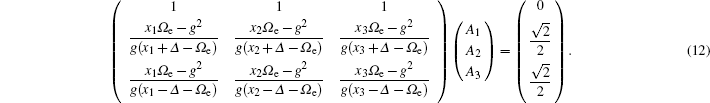
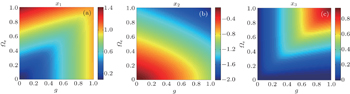
It is worth noting from Eqs. (10)–(13) that the time evolution behavior of the quantum state is determined cooperatively and competitively by the coupling interaction of the atom–cavity and the driving interaction of the atom-external field. From Eq. (4) each trial solution is a harmonic wave function and the quantum state of the strongly coupled system is the superposition of these harmonic states. The three eigenvalues, which involve the resonance frequency of the three harmonic oscillators from Eq. (10), play an important role in the dynamics of the quantum system. For this reason, we make a deep and systematic examination of their properties. We calculate these three eigenvalues each as a function of the interaction parameters of g and Ω_e using Eqs. (7) and (8), and the results are displayed in Fig. 2. For x₁, the influence of Ω_e is greater than that of g as can be seen from Fig. 2(a). In contrast, Ω_e and g have nearly the same effects on x₂ and x₃ in the entire parameter area, which can be found in Figs. 2(b) and 2(c). It is worth mentioning that x₂ decreases as both Ω_e and g grow, however, x₃ increases as both Ω_e and g grow. Generally speaking, each eigenvalue has a sensitive area, where the frequencies of the three harmonic oscillators are dominantly larger than those in other regions. Namely, for x₁, it is in the top left corner. For x₂, it is at the left bottom, and it is at the upper right for x₃. This means that the population transfer is very rapid and drastic between different quantum states in these three areas.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Calculated eigenvalues x1, x2, and x3 each as a function of the interaction parameters of g and Ωe, here g and Ωe are dimensionless.

Since the system involves two types of interactions, some detailed questions, such as the role of each type in shaping the single-excitation dynamics, the difference between the cases without and with external fields, need to be investigated. In the following we control the dynamics of population based on Eq. (13) by modulating the coupling strength (g) and Rabi frequency of the external field (Ω_e). The selected scope of the parameter value corresponds to the sensitive area in Fig. 2(b), i.e., the region where both Ω_e and g are small.

We assume that initially the atom is prepared in the superposition state of the two upper levels and the cavity is in a vacuum state as described in Eq. (11). In our calculations, the detuning between the transition frequency of the two upper levels and the resonant frequency of the cavity mode is set to be Δ₁ = − Δ₂ = Δ = 0.1. Firstly, we take a look at the population time evolution of a quantum system without the external field (Ω_e = 0) by changing the coupling constant g. The numerical results are shown in Fig. 3, where no approximation is made.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Time evolutions of population for the system only containing a three-level V-type atom and a single-mode cavity under different g values. The values of parameter g are 0.02 (a), 0.04 (b), and 0.06 (c). The time parameter t is dimensionless.

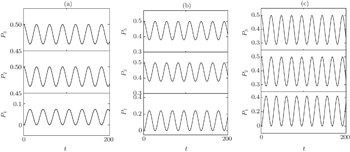
Obviously the atom–cavity system is located in the strongly coupling regime since dissipation is neglected. The spontaneous emission will occur, accompanied by the emission of a photon. Owing to strong coupling interaction, the emitted photon is trapped in the vicinity of the atom by the resonance cavity. The photon may be reabsorbed by the atom. Then the photon will be reemitted and reabsorbed a number of times before it leaves the cavity finally. Numerical results in Fig. 3 clearly demonstrate the periodic oscillatory behavior of the cavity photon and the atomic state dynamics: such an oscillation is the well-known vacuum Rabi oscillation. With the coupling coefficient g growing, which indicates that the coupling interaction strengthens, the population transfer from the upper levels to the lower lever increases correspondingly. Moreover, the population evolution of the upper levels abides by the same rule as time goes on because of the same initial condition and the same coupling coefficient between the two excited states and the ground state.

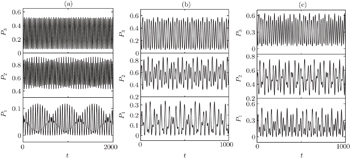
It is interesting to note that energy will not be fully transferred from the upper levels to the lower level every cycle. Perhaps this is due to the detuning between the atom and the cavity mode. As is well known, it is impossible for the three-level V-type atom to be in resonance with the cavity mode completely since there are two transition channels. However, it is easy for a two-level atom to be resonant with the cavity. Therefore, in order to understand the influence of the detuning on the population transfer in depth, we also give the numerical results about the dynamics of a two-level atom–cavity system. For the sake of distinguishing the detuning between the three-level atom and the two-level atom, here we denote the detuning of the two-level atom as Δ_two−level.

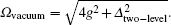
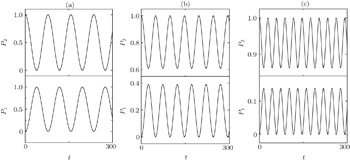The numerical results in Fig. 4 show the dynamics of the system containing a two-level atom interacting with a single-mode cavity under different detunings between the atom and the cavity mode. We assume that initially the atom is prepared in an excited state and the cavity is in a vacuum state, namely, P₁ (0) = 0 and P₂ (0) = 1. The coupling strength g is set to be 0.04. In the case of resonance as displayed in Fig. 4(a), the population is fully exchanged between the atom and the cavity photon in each cycle of time. In the case of detuning, the population transfer is not complete as seen in Figs. 4(b) and 4(c). Meanwhile, population transfer decreases when the detuning increases. The reason is that the interaction is strongest in the case of resonance, and weak in the case of large detuning. The above explanation is exactly the cause of incomplete population transfer between the upper levels and the lower level for the three-level atom. In addition, as the detuning increases, the frequency of oscillation increases obviously, which coincides with the equation of the vacuum Rabi frequency In contrast, the oscillation frequency increases slowly for the three-level atom when the parameter of g grows as shown in Fig. 3. The reason is that the value of g is quite small compared with the value of Δ.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Time evolutions of populations for the system containing a two-level atom interacting with a single-mode cavity under the Δtwo − level values of 0 (a), 0.1 (b), and 0.2 (c).

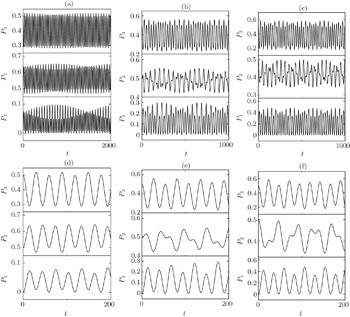
Now an external microwave field is added to induce the coupling between two excited states of the atom. For simplicity, we only consider the resonance case, i.e., the frequency of external field is equal to the frequency difference between upper levels (ν = |ω₂₁| = 2Δ). Therefore, Rabi frequency can be described as Ω_e = |D₁₂ |E₀/ħ, where D₁₂ is the dipole matrix element, E₀ is the amplitude of the external field, and ħ is the Planck constant. For a certain microwave field, D₁₂ is a fixed value, then Ω_e is proportional to E₀. In the following a series of time evolutions of population will be shown in Figs. 5–7 under different values of parameters g and Ω_e.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Time evolutions of the populations for the system containing a single-mode cavity and a three-level V-type atom driven by an external field with Rabi frequency Ωe = 0.02 under the g values of 0.02 (a), 0,04 (b), and 0.06 (c). The curves in panels (d)–(f) are the partially magnified curves in panels (a)–(c)

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Time evolutions of populations for the system containing a single-mode cavity and a three-level V-type atom driven by an external field with Rabi frequency Ωe = 0.04 and g values of 0.02 (a), 0.04 (b), and 0.06 (c).

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. Time evolutions of populations for the system containing a single-mode cavity and a three-level V-type atom driven by an external field with Rabi frequency Ωe = 0.06, and g values of 0.02 (a) 0.04 (b), and 0.06 (c).

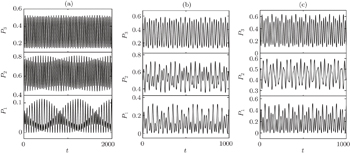
Rigorous numerical results are shown in Fig. 5 about the dynamics for the system containing a single-mode cavity and a three-level V-type atom driven by an external field with Rabi frequency Ω_e = 0.02 under different values of parameter g. In the case of no external field as shown in Fig. 3, the transition between the two excited states cannot happen. Nevertheless, when an external microwave field is added between the two upper states, the population transfer between the two upper states will occur, which leads to a series of interesting phenomena. Firstly, the population evolution of the two upper levels will no longer follow the same law as time goes on since populations of the two excited states are disturbed by the external field. Secondly, the population amplitude of the upmost state increases obviously, which indicates that a large quantity of population is transferred to the upmost state from the middle state in each cycle due to the driving effect of the external field. Thirdly, under the cooperative and competitive operation of the cavity photon and the external field, the general dynamics of the system is the superposition of a fast and a slow periodical oscillation. In order to see the details clearly, we also give the partially magnified curves. Comparing the results in Fig. 3 with the partially magnified curves in Figs. 3(d)–5(f), we find that the frequency of the fast oscillation does not change in the case of the same parameter g. This indicates the fast periodical oscillation results from the coupling effect of the cavity photon, and the external field specifically modulates the population intensity by contributing to the slow periodical oscillation. In addition, when the parameter g grows, the population transfer to the ground level increases and the population transfer to the middle level decreases because the coupling effect becomes gradually stronger.

In order to explain the role of the intensity of the external field more explicitly, the other two sets of results are shown in Figs. 6 and 7, where the Rabi frequencies of the external field (Ω_e) are set to be 0.04 and 0.06 respectively. It can be seen from Figs. 5–7 that the frequency of the slow oscillation becomes large gradually as the intensity of the external field increases. In the cases of smaller parameter g, which are demonstrated in Figs. 5(a)–7(a), the role of the microwave field is more dominant since the profile of the slow oscillation is more apparent. On the contrary, the effect of the cavity photon is more preponderant in the cases of larger parameter g, which are shown in Figs. 5(c)–7(c). In addition, the amplitudes of the two upper levels increase obviously as parameter Ω_e grows, which indicates that it is possible for the population transfer between the upper levels to be more complete as the intensity of the external field increases.

The mechanism of a cavity photon and microwave field on a V-type three-level is clarified through the above theoretical analysis and numerical results. Experiments adopting this scheme can also be performed since the technique of a microwave field irradiating a nanocavity involving atoms is well established and commonly used. Our theoretical model and results may provide a good reference to experimental details.

In this work, we consider a quantum system consisting of a three-level V-type atom driven simultaneously by a cavity photon and microwave field and examine systematically the time evolution of the atomic population. The system involves two types of interactions: the coupling effect of cavity field and the driving action of the external microwave field. Through analytical solution and rigorous numerical calculation, we find that the time evolution of population is strongly dependent on the atom–cavity coupling coefficient g and the Rabi frequency Ω_e that reflects the intensity of the external microwave field. Specifically, due to the coupling effect of the cavity photon, periodical oscillations of population between the two upper states and the ground state take place, which is the well-known vacuum Rabi oscillation. The population dynamics of the two upper states abide by the same rule as time goes on because of the same initial condition and the same coupling coefficient. As parameter g increases, the population transfer from the upper levels to the ground level increases correspondingly.

When an external microwave field is added to induce coupling between the two upper levels, the population exchange between these two levels can occur, which leads to a series of interesting phenomena. The population evolutions of the two upper levels will no longer follow the same law as time goes on. More population transfers to the upmost level in every cycle due to the driving effect of the external field. Under the cooperative and competitive operation of the cavity photon and the external field, the general dynamic of the system is the superposition of a fast and a slow periodical oscillation. The fast oscillation results from the effect of the cavity photon, and the microwave field leads to the slow oscillation, which modulates the population intensity. The frequency of the slow oscillation becomes large gradually as the intensity of the external field increases. In addition, the role of the microwave field is more dominant in the cases of smaller parameter g. On the contrary, the effect of the cavity photon is more preponderant in the case of larger parameter g.

Our theory and calculated results indicate that such a quantum system can provide a good platform to study cavity QED problems involving many freedoms of atom-field interaction since this system allows for the changing and tuning of each physical interaction parameter in a wide range. In this paper, only two parameters are discussed. A wider variety of new physical phenomena are expected when more parameters are considered, for instance, the detuning (δ) between the atom and the external field, the detuning (Δ) between the atom and the cavity field, and initial conditions. With a deeper insight into these fundamental problems, one can provide more methods to flexibly control atom-field interaction.