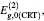Polar molecules bearing a permanent electric dipole moment (PDM) can provide strong, long-range, tunable, spatially anisotropic dipole–dipole interactions.^[1] They have potential applications from high precision metrology^[2] to chemical dynamics,^[3] quantum information processing,^[4] and the simulation of quantum many-body systems^[5] etc. The PDM reflects direct information about the electronic charge–density distribution of polar molecules, and could be quite different between various electronic states. The difference of PDM arises from the change of molecular orbital.^[6–9] For instance, in the alkaline earth-monohalides and -monohydrides, the decrease of PDM from the X²Σ state to the A²Π state is the result of the promotion of the sole unpaired valence electron from an s–p hybrid orbital to a more highly polarizable p–d hybrid orbital,^[6–8] while in the alkaline monohydrides LiH, it is the result of the promotion from an s orbital to an s–p hybrid orbital.^[9] Another type of giant dipole molecules are organic molecules with the delocalized conjugated π electrons. Such molecules often have excited electronic states of a charge transfer character, so there can be large differences of PDM between the electronic ground and excited states.^[10] The interaction of a two-level polar molecule with a classical optical field has been studied by many researchers.^[11–14] It is shown that the nonzero difference of PDM between the electronic ground and excited states can significantly affect the coupling between the polar molecule and the optical field, and is responsible for some new optical properties which are quite different from a regular atomic system, for instance, multi-photon transition,^[15] nonlinear optical properties,^[16] high harmonic generation,^[17] etc.

On the other hand, the study of strong coupling between the matter and the cavity field through quantum electrodynamics (QED), in which the interaction strength exceeds the optical transition and cavity-mode damping rates, has been the subject of great interest.^[18] It has broad applications ranging from metrology^[19] and quantum computation^[20] to a mechanism for cooling atoms and molecules,^[21] etc. Nowadays, the researchers have achieved the strong coupling in different physical systems, such as the atomic system,^[22] semiconductor quantum dot microcavity,^[23] superconducting qubit circuit QED,^[24] and organic microcavity.^[25] Also, the possibility of cavity-assisted laser cooling of polar molecules has been theoretically proposed.^[26] However, among the above-mentioned cavity QED interactions, little attention has been paid to the effect of the permanent dipole difference between the ground state and excited state of the molecules which usually plays a role in the nonlinear process. Our motivation is to study the effect of permanent dipole difference in the field of strong coupled polar molecule cavity QED.

For the early work on strong coupled cavity QED, the coupling strength λ was much smaller than the cavity–field frequency ω_c (typical values for atom–cavity QED experiments are λ/ω_c ∼ 10^−5[27]). The interaction can therefore be well described by the Jaynes–Cummings (JC) model within the rotating-wave approximation (RWA). But recent experimental progress has reached the ultrastrong-coupling regime, for example, the normalized coupling strength λ/ω_c for polyelec-trolyte/J aggregate dye coupled with an optical microcavity has reached 0.1.^[25] In this case, the counter-rotating wave terms (CRT) of the interaction cannot be neglected and result in a Bloch–Siegert (BS) shift of the resonant frequency, which has been observed recently in the experiment.^[24] Therefore, the interaction of matter and the cavity field is then governed by the Rabi model beyond the RWA. Because of the difficulties in obtaining the exact solution of the Rabi model, some approximate analytical and numerical approaches have been proposed^[28–31] and the BS shift in atomic and superconducting qubit cavity QED have been studied.^[32,33]

For the strong coupled polar molecule cavity QED system, the contribution of PDM should be considered on the basis of CRT.^[34] Because the JC-type Hamiltonian can be solved analytically in a closed form in the basis of |e,n〉 and |g,n + 1〉 (where the qubit states |e〉 and |g〉 are the excited state and ground state respectively, and the oscillator states |n〉 are Fock states) in terms of dressed-states,^[35] we can treat the contribution of PDM and CRT as a perturbation of interaction. In our work, a dressed-state perturbation theory (DSP) beyond the RWA is proposed to treat analytically a two-level polar molecule coupled to a quantized cavity field. Based on our DSP theory, the BS shift in the polar molecule cavity QED system is also obtained, which includes the contribution of both CRT and PDM separately. The BS shift caused by the CRT is approximately proportional to the square of the coupling strength, while the BS shift caused by the PDM is proportional to the square of the normalized permanent dipole difference and is dependent on the higher terms of λ, which is coincident with Ref. [34]. In addition, for the transition between the higher excited state and the ground state, the magnitude of the BS shift becomes larger as the energy level increases. Also, our method can be extended to the solution of the two-level atom Rabi model Hamiltonian beyond the RWA by setting the normalized permanent dipole difference equal zero.

The paper is organized as follows. In Section 2, we present the DSP theory and derive analytical expressions for the eigenenergies and eigenstates of a two-level polar molecule cavity QED system. The validity of our approach up to the second-order correction is also given. In Section 3, we show the transition relation between different energy levels through their populations, and the respective contribution of PDM and CRT to the transition is given as well. In addition, by comparing the energy spectrum obtained by our approach with those by numerical simulation, we furthermore clarify the validity of our method. The effects of PDM and CRT on the energy level shift are analyzed separately. Finally, conclusions are drawn in Section 4.

In this paper, we focus on the coupling of electronic transition (such as alkaline-earth monohalides,^[6,7] alkaline-earth monohydrides,^[8] alkaline monohydrides,^[9] giant dipole diphenyl molecules,^[10] etc.) with the visible laser field. As for the coupling of the vibrational transition or rotational transition of a polar molecule with a cavity field, which are not dealt with here, they will be discussed in our future work. When the frequency of the relevant cavity mode ω_c is near resonant with a polar molecule’s transition frequency ω₀ between the electronic ground state and excited state, the dynamics of the molecule are restricted to the two state {|g〉,|e〉}, and the molecule is well approximated by a two-level system.

The interaction between a two-level polar molecule and a quantized cavity field with frequency ω_c is described by:^[34]

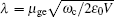
We consider the Hamiltonian can be divided into two parts:

First, we can obtain energy eigenstates of the unperturbed system through the diagonalization of the non-perturbation part Hamiltonian where detuning δ = ω₀ − ω_c, Rabi frequency The corresponding eigenenergies are: |g,0〉 is also a eigenstate of H₀ with eigenenergy −ω_0/2. These energy eigenstates form a orthogonal and normalized completed set:

Since these unperturbed eigenstates are completed, the explicit state |Ψ〉 of H can be expanded in terms of the eigenfunction set as:

Suppose that the system is in one of the eigenstates before being perturbed, which means that zero-order approximated wave function is and zero-order approximated energy is Based on the framework of perturbation theory, analytical approximations for the wave function and the energy of the dressed-state after being perturbed can be performed systematically. The ground-state wave function and energy can be obtained as (all of them are up to the second-order correction):

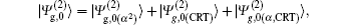
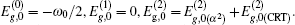
All of the above results can be obtained by straight but complex calculation, and the detailed expression of the ground state wave function |Ψ_g,0〉 is given in Appendix B. Of course, according to a similar procedure, we can also get the wave function of the higher order dressed-state but not all of them are shown here, and only the first-order wave function corrections are shown in Appendix C. In all of these analytical expressions, correspond to the contribution of PDM of polar molecule, correspond to the contribution of CRT, and correspond to the combined contribution of both the PDM and the CRT. Where the first-order wavefunction corrections are proportional to α, and the first-order energy corrections equal zero; while the second-order wavefunctions and energy corrections are proportional to α², and are proportional to α. In particular, when α = 0, all of these results reduce to those of the two-level atom Rabi model case, hence the DSP theory is also a new analytical method to treat the atom Rabi model.

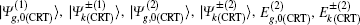
In the following, we will discuss the validity of our approach. The definite meaning of a small H′ is that the matrix element of the perturbation operator between the perturbing state and the unperturbed state should be much smaller than the energy difference between the two states: Thus, the power series of E and |Ψ〉 will convergence quickly, and we only need to calculate the first few terms to obtain quite accurate results. Through calculation, our DSP theory up to the second-order correction is valid in a certain range of both normalized coupling strength f = λ/ω_c and in the resonant case, and the range of validity of α narrows as the f value increases. In addition, we focus on coherent coupling here in this DSP theory, and the involvement of decay of both the cavity field and the molecule will be discussed in our future paper.

In this section we will discuss the effect of PDM on the energy level and population of the system. The energy levels of the system are displayed in Fig. 1. The first column stands for the uncoupled stystem, while the second column stands for the dressed energy levels for the unperturbed system under the RWA, and the third column stands for the dressed energy levels for the perturbed system beyond the RWA. Suppose the system is in one of the eigenstates before being perturbed, for example in the ground state |g,0〉. Under the framework of the RWA, the ground state of the system is always uncoupled from other states and thereby remains unchanged. Yet when the CRTs and PDM are involved in the treatment, the ground state will always overlap with the upper level and the photon in the ground state is no longer in a vacuum state, but now contains molecule–cavity coupling.^[36] Under the first-order perturbation, the PDM leads the coupling between the states |g,0〉 and while the CRT leads the coupling between state |g,0〉 and according to Appendix (B1–B2). Furthermore, under the second-order perturbation, the PDM induces the transition between the states and and while the CRT induces the transition between the states and and according to the appendix. With the increase of the order of the perturbations, there will be coupling between the higher order dressed states.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. The dressed energy level of the system. The black solid arrows correspond to the coupling produced by the rotating wave terms, the blue dashed arrows correspond to the coupling mainly produced by the CRT and the red dotted arrows correspond to the coupling mainly produced by the PDM.

In order to make the transition relation between the energy levels more explicit, we can furthermore expand the dressed energy level in terms of {|e,n〉,|g,n + 1〉}. The population probability of the ground state |g,0〉 and higher energy levels |e,n〉,|g,n + 1〉 (n = 0,1,2,3) against the normalized coupling constant f = λ/ω_c for different α in the resonant case are exhibited in Fig. 2. In the whole paper, we set ω_c = 1 for simplicity. As shown in Fig. 2(a), when the coupling strength becomes greater, the population probability of the ground state |g,0〉 will decrease, and the higher order states’ population probability will increase, yet the populations of the higher order states are much smaller than that of the lower order one according to Figs. 2(b)–2(i). Besides, when α = 0, the CRT leads the couplings between the state |g,0〉 and and as shown in Figs. 2(a), 2(d), 2(e), 2(h), and 2(i), while the PDM furthermore leads the couplings between the state |g,0〉 and and and As |α| increases, the coupling between the dressed states will strengthen.

Fig. 2.

Figure Option ViewDownloadNew Window

Fig. 2. The population probability of different energy levels (a) |g,0〉, (b) |g,1〉, (c) |e,0〉, (d) |g,2〉, (e) |e,1〉, (f) |g,3〉, (g) |e,2〉, (h) |g,4〉, (i) |e,3〉 against the normalized coupling constant f = λ/ωc for different α in the resonant case. Red solid lines represent α = 0, blue dotted lines represent |α| = 0.5, and green dot–dashed lines represent |α| = 1. In panels (e), (h), and (i), the differences among the curves are very small.

Below we will present a detailed discussion on the energy spectrum of the polar molecule cavity QED system for various values of f and α to further demonstrate the validity of our analytical approach. Figure 3 shows the seven lower-lying energy levels as a function of f, α, and detuning δ, respectively. We compare eigenvalues obtained by our DSP theory with those by numerical diagonalization in a truncated finite-dimensional Hilbert space.^[37] It is shown that for the parameter regimes with f < 0.1, |α| < 1, and a wide range of detuning values −1 < δ/ω_c < 1, our analytical energy spectrums are in good agreement with the direct numerical simulation. Therefore, the DSP theory provides an accurate analytical expression to the energy spectrum of the two-level polar molecule cavity QED system in a certain range of both f and α values. Note that in the present experimentally accessible systems the maximum value for the coupling strength is generally realized in the superconducting circuit resonator^[24] and organic microcavity,^[25] which is around f ∼ 0.1. So it should be practically interesting to find a good solution in this coupling regime. As for the case of an ultrastrong coupling regime, we will discuss it in our future work.

Fig. 3.

Figure Option ViewDownloadNew Window

Fig. 3. The seven lower-lying energy levels Eg,0, k = (0,1,2) as a function of f, α, and detuning δ, respectively. (a) δ = 0, |α| = 1; (b) δ = 0, f = 0.01,0.1; (c) |α| = 1, f = 0.05. In panels (a) and (c), blue dot–dashed lines represent the results of our dressed perturbation theory, while red solid lines represent the results of numerical simulation. In panel (b), dot–dashed lines represent the results of dressed perturbation theory, solid lines represent the results of numerical simulation, red and blue lines represent the energy spectrum of f = 0.01, and black and green lines represent the energy spectrum of f = 0.1. For the parameter regimes with f < 0.1, |α| < 1, and a wide range of detuning values −1 < δ/ωc < 1, our analytical energy spectrums are in good agreement with the direct numerical simulation.

In Fig. 3(a), when f = 0, the ground state is nondegenerate and each higher energy level is doubly degenerate. The separation between the levels is ω_c, which is also equal to ω₀ in the resonant case. As f increases, the energies of the ground state E_g,0 and gradually decrease, while the energies of gradually increase within the valid regime f < 0.1. The effect of different atom–photon coupling on the energy spectrum within 0 ≤ |α| ≤ 3 are shown in Fig. 3(b); the larger coupling leads to the smaller valid regime of α, which is coincident with the valid condition of dressed state perturbation theory, and there are small variations of the energies within the valid regime of α. In Fig. 3(c), the energy spectrum exhibits avoided crossings adjacent to δ = 0. The shift of the resonance frequency is a so-called BS shift,^[32] which could also be described by the energy shift of the level transition with the consideration of the CRT in the strong coupling regime.^[24,33] For instance, in Ref. [32], they noted that CRTs yield the second-order corrections in coupling strength to the resonance frequency. Also, in Ref. [34], it is shown that the terms higher than the second order of laser Rabi frequency in the BS shift cannot be neglected for giant-dipole (large permanent dipole difference) molecules under an intense oscillating field. We will discuss the magnitude of it in detail in the following passage.

From the analytical expressions of the energy level Eqs. (10)–(15), we can also find that both the CRT and the PDM result in the energy level shift from the unperturbed energy, and the magnitude of the energy level shift is dependent on the coupling strength λ, the normalized permanent dipole difference α, the cavity field frequency ω_c, the molecule transition frequency ω₀, and the photon number k, where the energy shift induced by the CRT is approximately proportional to the λ², and the energy shift induced by the PDM is proportional to α².

In Fig. 4(a), we plot the respective contributions of the PDM and the CRT in the energy shift of the five lower-lying energy levels E_g, as a function of α² for f = 0.05 in the case of exact resonance δ = 0. For a polar molecule with relatively small |α|, the contribution of the PDM in the energy shift is less than that of the CRT, while for some aromatic molecules frequently used in lasers and nonlinear optics^[38] and organic compounds presenting significant nonlinear optical properties,^[39] the PDM difference between the electronic excited state and ground state can be very large, which is the so-called giant dipole molecule, |α| value which can well exceed 1. Then from Fig. 4(a), the contribution of the PDM in the energy shift can surpass that of the CRT. This conclusion can be also drawn from Fig. 4(b). The BS shift can be also obtained by means of Eqs. (10)–(15). In Fig. 4(b), the smallest BS shift of the transition for the different α as a function of λ² with detuning δ = 0 is plotted. It is shown that the BS shift caused by the CRT is approximately proportional to λ², and those caused by the PDM are dependent on the higher terms of λ. For a giant dipole molecule, the contribution of the PDM can produce a greater BS shift than that of the CRT, especially with the increasing coupling strength λ. The total BS shift caused by the PDM and the CRT with the transition for |α| = 1 as a function of λ² with detuning δ = 0 is shown in Fig. 4(c). For the transition between the higher excited state and the ground state the magnitude of the BS shift becomes larger as k increases, and its sign changes alternatively with ∓.

Fig. 4.

Figure Option ViewDownloadNew Window

Fig. 4. (a) The respective contributions of the PDM and the CRT in the energy shift of the five lower-lying energy levels as a function of α2 for f = 0.05 in the resonant case, where those curves parallel to the abscissa axis represent an energy level shift caused by the CRT. The black lines: and the red lines: and the blue lines: and the green lines: and the magenta lines: and (b) The BS shift of the transition for the different α as a function of λ2 with detuning δ = 0. (c) The total BS shift caused by PDM and CRT with the transition for |α| = 1 as a function of λ2 with detuning δ = 0.

The parameters used for calculation here are within the range of practical molecules. For instance, in the coupling of electronic transitions of SrF^[6,7] and diphenyl molecules [N(CH₃)₂ − C₆H₄ − (C ≡ C)₂ − C₆H₄ − NO₂]^[10] with visible field, we calculate the BS shift of the transition caused by the PDM and CRT, respectively for f = 0.05 in the resonant case, and the results are given in Table 1. With a greater α, the contribution of the PDM can produce a greater BS shift than that caused by the CRT.

Table 1.

Table 1.

Table 1. The BS shift (in unit cm−1) caused by the PDM and CRT in the coupling of electronic transitions of polar molecules with visible field. f = λ/ωc = 0.05 in the resonant case ωc = ω0. . Molecule Transition (μgg,μee,μge (D)) α ω0/cm−1 PDM shift CRT shift SrFa X2Σ − A2Π (3.482, 2.059, 6.227) –0.114 1.52 0.091 0.454 Diphenylb (1-2) (10.67, 16.66, 9.13) 0.328 3.05 1.53 0.91 (1-4) (10.67, 12.99, 3.9) 0.297 3.85 1.57 1.151 (1-7) (10.67, 14.07, 3.37) 0.504 4.89 5.65 1.461 a Refs. [6], [7]. b Ref. [10].

Table 1. The BS shift (in unit cm−1) caused by the PDM and CRT in the coupling of electronic transitions of polar molecules with visible field. f = λ/ωc = 0.05 in the resonant case ωc = ω0. .

In the present paper, we apply the dressed-state perturbation theory beyond the RWA to investigate the interaction between a two-level polar molecule and a quantized cavity field. Analytical expressions have been derived for both the ground state and the excited state energy spectrums and wave functions of the system, where the contribution of permanent dipole moments and the counter-rotating wave term can be shown separately. The validity of our approach is discussed by comparison with the numerical diagonolization method. For the parameter regimes with f < 0.1, |α| < 1, and a wide range of detuning values −1 < δ < 1, our analytical results agree well with the direct numerical simulation. It implies that our presented DSP theory is valid for the current experimental conditions with strong coupling. From the expression of the wave function, we can clearly obtain the population of the different dressed-state energy levels and the transition relations between the energy levels. The respective effects of the PDM and CRT on both the population and energy level of the system are analyzed. Compared with the CRT coupling, the PDM induces the coupling of more dressed states, and as |α| increases, the coupling between the dressed states will strengthen. Furthermore, both the CRT and the PDM result in the energy shift of the dressed states from those of the JC model Hamiltonian, and the energy shift caused by the CRT is approximately proportional to the square of the coupling strength, while the energy shift caused by the PDM is proportional to the square of the normalized permanent dipole difference and is dependent on the higher terms of the coupling strength. For a giant dipole molecule cavity QED, it is expected that the contribution of the permanent dipole moment could produce a greater BS shift than that of the counter-rotating wave term. Moreover, our method can also be extended to the solution of the two-level atom Rabi model Hamiltonian beyond the RWA by setting α = 0.

In addition, much theoretical and experimental attention has been devoted to the effect of the counter-rotating wave terms, which plays an important role in the strong-coupling regime and results in some novel quantum mechanical phenomena, for instance, the modification of the dynamics of population inversion,^[40] preparing a non-classical state,^[41] quantum irreversibility and chaos,^[42] quantum phase transition,^[43] the simulation of the dynamical Casimir effect in a semiconductor microcavity or superconducting circuit QED,^[44] and the production of photons from a vacuum,^[45] etc. Comparing the contribution of the permanent dipole moment with that of the counter-rotating wave terms will lead to beneficial discussion, and we will work on it in a future paper.