Cite this Article
Yu Weihao, Zhao Ruihuang, Deng Fu, Huang Jiayao, Chen Chidao, Yang Xiangbo, Zhao Yanping, Deng Dongmei. Propagation of Airy Gaussian vortex beams in uniaxial crystals. Chinese Physics B, 2016, 25(4): 044201  
Permissions
Propagation of Airy Gaussian vortex beams in uniaxial crystals
Yu Weihao1, Zhao Ruihuang1, Deng Fu1, Huang Jiayao1, Chen Chidao1, Yang Xiangbo1, Zhao Yanping1, Deng Dongmei1, 2, †,
Guangdong Provincial Key Laboratory of Nanophotonic Functional Materials and Devices, South China Normal University, Guangzhou 510631, China
CAS Key Laboratory of Geospace Environment, University of Science and Technology of China, Chinese Academy of Sciences (CAS), Hefei 230026, China

 

† Corresponding author. E-mail: dmdeng@263.net

Project supported by the National Natural Science Foundation of China (Grant Nos. 11374108, 11374107, 10904041, and 11547212), the Foundation of Cultivating Outstanding Young Scholars of Guangdong Province, China, the CAS Key Laboratory of Geospace Environment, University of Science and Technology of China, the National Training Program of Innovation and Entrepreneurship for Undergraduates (Grant No. 2015093), and the Science and Technology Projects of Guangdong Province, China (Grant No. 2013B031800011).

Abstract
Abstract

The propagation dynamics of the Airy Gaussian vortex beams in uniaxial crystals orthogonal to the optical axis has been investigated analytically and numerically. The propagation expression of the beams has been obtained. The propagation features of the Airy Gaussian vortex beams are shown with changes of the distribution factor and the ratio of the extraordinary refractive index to the ordinary refractive index. The correlations between the ratio and the maximum intensity value during the propagation, and its appearing distance have been investigated.

PACS: 42.25.Bs;42.25.–p;
Keyword:Airy Gaussian vortex beams;uniaxial crystals;anisotropic effect;
1. Introduction

In 1979, Berry and Balazs introduced the nonspreading Airy wave packets by solving Schrödinger equation.[1] The packets bring many researchers’ interests due to their unique properties of nonspreading and constant acceleration in free space. In 2007, on the basis of previous studies, Siviloglou et al. obtained finite energy Airy beams by adding a decay factor. They investigated and observed those beams in both one- and two-dimensional configurations theoretically[2] and experimentally,[3] finding that the finite energy Airy beams also preserve quasi-diffraction-free and free acceleration properties. Next year, self-healing properties were investigated by John Broky et al.[4] Then Airy beams were widely investigated in many kinds of materials such as free space,[5–7] right-handed material to left-handed material,[8] bulk nonlinear media,[9–15] and a quadratic-index medium.[16] Nowadays, researches on Airy beams are involved in various fields of military,[17–19] micro–nano technology,[20–23] atmospheric sciences,[24] and so on.

Furthermore, it is an interesting subject to describe the light propagation in the anisotropic media in both theoretical and applied optics.[25,26] In reality, crystals play an important part in the design of optical devices, e.g., polarizers and compensators, because of their ability to affect the polarization state of light.[27] Through uniaxial crystals, the propagation of Airy beams,[28] Airy vortex beams,[29] and Airy Gaussian beams[30] has been investigated.

Airy Gaussian vortex beams (AiGVBs) are obtained from Airy beams multiplied Gaussian factor and vortex factor. It is intriguing for AiGVBs that these beams not only have the unique features of Airy Gaussian beams:[31,32] free acceleration and self-healing, but also have the properties of vortex beams:[33,34] intensity singularities and phase singularities. However, to the best of our knowledge, AiGVBs only have been investigated in the media of right-hand materials and left-hand materials.[34] Therefore, in the rest of the paper, the propagation of AiGVBs in uniaxial crystals is to be investigated.

2. Propagation of Airy Gaussian vortex beams in uniaxial crystals

In the spatial coordinate system, the z axis is taken to be the propagation axis and the x axis is taken to be the optical axis of the uniaxial crystal. The observation plane is taken to be z and the input plane is z = 0. The relative dielectric tensor ε of the uniaxial crystal is set as

where ne and no are the extraordinary and the ordinary refractive indices of the uniaxial crystal. The electric field distribution of the AiGVBs in the input plane z = 0 reads

where Ex(x0, y0,0) and Ey(x0, y0,0), respectively, stand for the initial electric field distribution in the x and y directions; A0 is the amplitude of the beams; Ai(·) is the Airy function; χ0 is a distribution factor which can be non-zero real number (for simplicity, we only value it positive real number in this paper); ax and ay, respectively, stand for decay factors in the x and y directions which make the energy of the beams be finite; w stands for the beam width of Gaussian beams; ((x0 – x1)/χ0w + i(y0 − y1)/χ0w)m is the positive vortex factor, while ((x0 − x2)/χ0w − (y0 − y2)/χ0w)n is the negative one, m and n are orders of their factor, respectively, x1, y1 and x2, y2, respectively, stand for positions from the center of the positive and negative vortex factors. However, for simplicity, in this paper, we only discuss a situation with m = 1, n = 0, and x1 = y1 = x2 = y2 = 0. Hence, the initial electric field distribution of AiGVBs in this paper reads

Under the paraxial approximation, the propagation formulas of the AiGVBs orthogonal to the axis can be obtained by[27,28,35]

where k = 2π/λ is the wave number and λ is the optical wavelength. Substituting Eqs. (1) and (3) into Eqs. (4) and (5), and using Airy integral formulas

the analytical complex field of AiGVBs after propagating a distance z in uniaxial crystals orthogonal to the optical axis can be obtained as

where

As for expressions (11)–(14), where

3. Numerical calculations and analyses

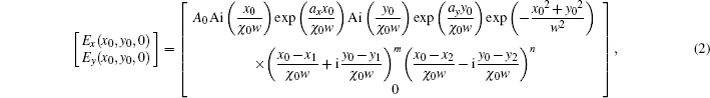
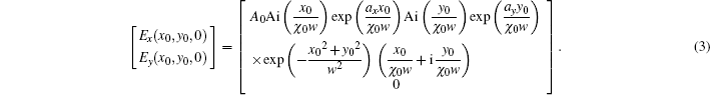
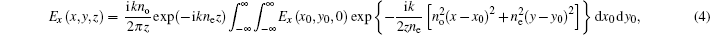
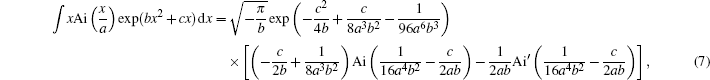
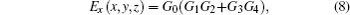
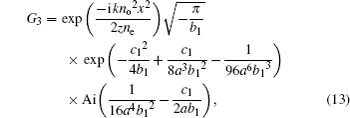
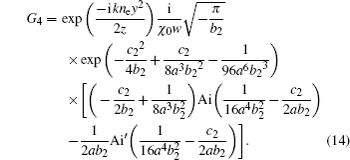
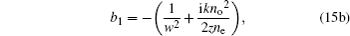
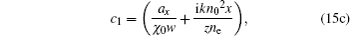
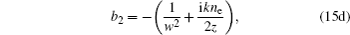
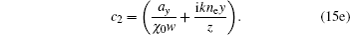
Here we investigate how the changes of χ0 and ne/no affect the propagation of AiGVBs in uniaxial crystals. The beam parameters are chosen as follows: λ = 530 nm, ax = ay = 0.1, the normalized coefficient X0 = λw = 10−4 m, the Rayleigh distance 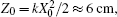and no = 2.616. Hereafter, these parameters will not change.

First, we will consider the case of different χ0. We set no = 3.1392 and intensity I(x,y,z) = |Ex(x,y,z)|2. At each observation plane, we normalize the values of intensity with

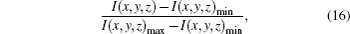
where I(x,y,z) means the value of the intensity at the observation plane z, and I(x,y,z)max or I(x,y,z)min means the maximum or the minimum value of the intensity at that plane.

From Figs. 1 and 2, we can find that if χ0 takes smaller number, the distributions of the intensity and the phase approach the distributions of Airy vortex beams, like Figs. 1(a1) and 2(a1), while if χ0 takes larger number, the distributions approach those of Gaussian vortex beams, like Figs. 1(a3) and 2(a3). The smaller χ0 is, the more largely the Airy factor affects, and on the contrary, the more largely the Gaussian factor affects. The Gaussian factor can strengthen main lobes and weaken side lobes, but the vortex factor can weaken main lobes, like Figs. 1(a1), 1(b1), and 1(c1). In the propagation process, figures 1(a2), 1(b2), and 1(c2) show that AiGVBs heal firstly and each main lobe is rebuilt when z = 8Z0, z = 5Z0, and z = 3Z0, demonstrating that the healing distance decreases as χ0 increases. After healing, main lobes further strengthen and the energy of side lobes converges into main lobes until most energy is concentrated on the main lobes, like Figs. 1(a3), 1(b3), and 1(c3). Then the energy flows along the x and y directions, but the energy flows along the x direction more largely due to ne > no. In further propagation, the energy mostly distributes along the x direction.

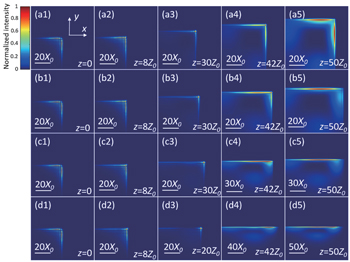
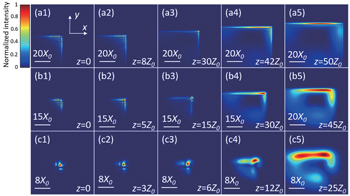Fig. 1. Normalized intensity distribution of AiGVBs propagating in the uniaxial crystals at several observation planes. (a1)–(a5) χ0 = 0.01, (b1)–(b5) χ0 = 0.1, and (c1)–(c5) χ0 = 0.3.
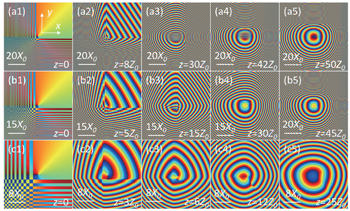Fig. 2. Phase distribution of AiGVBs propagating in the uniaxial crystals at several observation planes. (a1)–(a5) χ0 = 0.01, (b1)–(b5) χ0 = 0.1, (c1)–(c5) χ0 = 0.3.

Then, we investigate the maximum intensity of each observation plane (different z) of the AiGVBs with different χ0 (see Fig. 3). It shows that if χ0 is smaller, the beams approach Airy vortex beams, so the maximum intensity firstly increases as the distance increases, corresponding to the healing process. If χ0 is larger, the effect of the Gaussian factor enhances, causing the beams to diffract rapidly, so the maximum intensity decreases rapidly.

Fig. 3. Maximum intensity of each observation plane (different z) of the AiGVBs with different χ0.

Next, we will investigate how the change of ne/no affects the propagation of AiGVBs in uniaxial crystals. Here, we set χ0 = 0.01 and no = 2.616. The normalized intensity and the phase distributions with different values of ne/no are shown in Figs. 4 and 5.

Fig. 4. Normalized intensity distribution of AiGVBs propagating in the uniaxial crystals at several observation planes. (a1)–(a5) ne/no = 1, (b1)–(b5) ne/no = 1.2, (c1)–(c5) ne/no = 1.5, and (d1)–(d4) ne/no = 2.
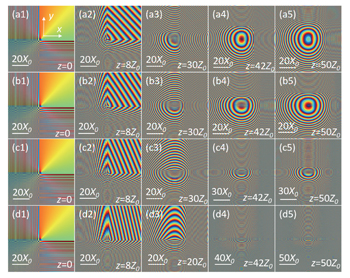Fig. 5. Phase distribution of AiGVBs propagating in the uniaxial crystals at several observation planes. (a1)–(a5) ne/no = 1, (b1)–(b5) ne/no = 1.2, (c1)–(c5) ne/no = 1.5, and (d1)–(d4) ne/no = 2.

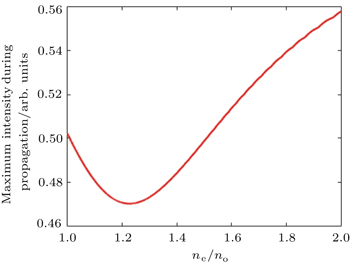
The two figures show that the value of ne/no has a great impact on the distributions of the intensity and the phase. Figures 4(a1)–4(a4) show that if ne = n0, the intensity distribution along the x direction equals that in the y direction. As the value of ne/no decreases, the energy more obviously distributes along the x direction. As for the phase, figure 5 shows that as the value of ne/no decreases, the phase looks more like an ellipse spiral shape.

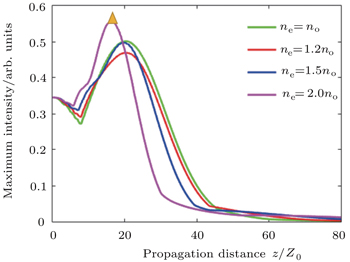We continue to investigate the maximum intensity values of each observation plane (different z) of the AiGVBs with different values of ne/no. Some results are shown in Fig. 6. We find that the maximum intensity value during the propagation and its appearing distance z are not monotonic with the ratio of ne/no. As for what are the maximum intensity value during the propagation and its appearing distance z, for example, in the propagation of the beam with ne = 2.0n0 in Fig. 6, the values on horizontal and vertical coordinates that the point A corresponds to are the maximum value and its appearing distance z. We further investigate, and the results are showed in Figs. 7 and 8.

Fig. 6. Maximum intensity of each observation plane (different z) of the AiGVBs with different values of ne/no.
Fig. 7. Maximum intensity value during propagation with different values of ne/no.
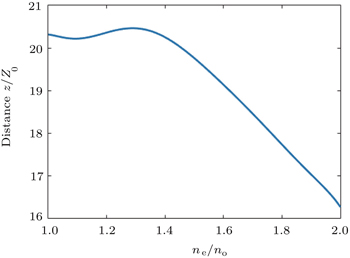Fig. 8. Appearing distance z of the maximum intensity value during propagation with different values of ne/no.

Figure 7 shows that as ne/no increases, the maximum intensity value during the propagation firstly decreases then increases. The minimum intensity appears when ne = 1.23n0. As discussed above, Airy factor makes the energy of the AiGVBs concentrate to the center while the increase of ne/no makes the energy more distribute along with the x direction. Although these two effects both concentrate the energy, to some extent, the direction of concentrating the energy of the two effects is different. The increase of ne/no firstly will weaken the effect of Airy factor of concentrating the energy to the center, so the maximum intensity value during the propagation decreases as ne/no increases firstly. Then, as ne/no increases, the effect of ne/no becomes larger than the effect of Airy factor, so after ne/no = 1.23, the maximum intensity value increases with the increase of ne/no. The correlation between the appearing distance z of the maximum value and ne/no is also not monotonic, too. The general trend is that the appearing distance z of the maximum value firstly decreases, next increases, and then decreases as ne/no increases.

4. Conclusions

The propagation dynamics of the Airy Gaussian vortex beams in uniaxial crystals orthogonal to the optical axis has been investigated analytically and numerically. The propagation expression of the beams has been obtained. The propagation features of the beams with changes of the distribution factor χ0 and the ratio of the extraordinary refractive index ne to the ordinary refractive index no are showed. When χ0 is valued smaller, the distributions of the intensity and the phase approach to the distributions of the Airy vortex beams, and on the contrary, the distributions approach to those of the Gaussian vortex beams. The ratio ne/no affects the distributions of the intensity and the phase, as well as the maximum intensity value of each observation plane, the maximum intensity value during the propagation and its appearing distance. However, the correlations between the ratio and the maximum intensity value during the propagation, between the ratio and the appearing distance are not monotonic.

Reference
1Berry M VBalazs N L 1979 Am. J. Phys. 47 264
2Siviloglou G AChristodoulides D N 2007 Opt. Lett. 32 979
3Siviloglou G ABroky JDogariu AChristodoulides D N2007Phys. Rev. Lett.99
4Broky JSivilogou G ADogariu AChristodoulides D N 2008 Opt. Express 16 12880
5Deng D MGuo Q 2009 New J. Phys. 11 103029
6Ren Z JYing C FFan C JWu Q 2012 Chin. Phys. Lett. 29 124209
7Deng D MDu S LGuo Q 2013 Opt. Commun. 289 6
8Lin H CPu J X 2012 Chin. Phys. 21 054201
9Deng DLi H 2012 Appl. Phys. 106 677
10Zhang Y QBelic M RWu Z KZheng H BLu K QLi Y YZhang Y P 2013 Opt. Lett. 38 4585
11Zhang Y QBelic M RZheng H BChen H XLi C BLi Y YZhang Y P 2014 Opt. Express 22 7160
12Zhou G QChen R PRu G Y 2014 Laser Phys. Lett. 11 105001
13Driben RKonotop V VMeier T 2014 Opt. Lett. 39 5523
14Shen MGao J SGe L J 2015 Sci. Rep. 5 9814
15Chen C DChen BPeng XDeng D M 2015 J. Opt. 17 035504
16Deng D M 2011 Eur. Phys. J. 65 553
17Chong ARenninger W HChristodoulides D NWise F W 2010 Nat. Photon. 4 103
18Abdollahpour DSuntsov SPapazoglou D GTzortzakis S 2010 Phys. Rev. Lett. 105 253901
19Ren Z JWu QZhou W DWu G ZShi Y L2012Acta Phys. Sin.61174207(in Chinese)
20Christodoulides D N 2008 Nat. Photon. 2 652
21Baumgartl JMazilu MDholakia K 2008 Nat. Photon. 2 675
22Zhang PPrakash JZhang ZMills M SEfremidis N KChristodoulieds D NChen Z G 2011 Opt. Lett. 36 2883
23Zhang ZZhang PMills MChen Z GChristodoulides D NLiu J J 2013 Chin. Opt. Lett. 11 033502
24Gu Y LGbur G 2010 Opt. Lett. 35 3456
25Yariv AYeh P1984Optical waves in crystalsNew YorkWiley
26Chen H C1983Theory of electromagnetic wavesNew YorkMcGraw-Hill
27Born MWorf E1999Principles of optics7th edn.OxfordPergamon
28Zhou G QChen R PChu X X 2012 Opt. Express 20 2196
29Deng D MChen C DZhao XLi H G 2013 Appl. Phys. B-Lasers Opt. 110 433
30Zhou M LChen C DPeng XPeng Y LDeng D M 2014 Chin. Phys. 24 124102
31Hang J YLiang Z JFu DengYu W HZhao R HChen BYang X BDeng D M 2015 J. Opt. Soc. Am. 32 2104
32Bandres M AGutierrez-Vega J C 2007 Opt. Express 15 16719
33Chen BChen C DPeng XPeng Y LZhou M LDeng D M 2015 Opt. Express 23 19288
34Chen BChen C DPeng XDeng D M 2015 J. Opt. Soc. Am. 32 173
35Ciattoni APalma C 2003 J. Opt. Soc. Am. 20 2163