Cross sections for the electronic excitation of molecules by electrons impact play an important role in many fundamental areas such as the plasma process, radiation science, astrophysics and planetary atmospheres. Nevertheless, the measurement of reliable cross sections for electronic excitations in molecules remains a difficult challenge for researchers working in this area. Even for the simplest diatomic target, the H₂ molecule, the number of experimental measurements is small. Differential cross sections (DCS) for the excited states are measured by Trajmar et al.,^[1] Weingartshofer et al.,^[2] Hall and Andric,^[3] Khakoo et al.,^[4] Khakoo and Segura,^[5] and Wrkich et al.^[6] On the theoretical side, the calculation of accurate cross sections for such processes is also far from satisfactory. Several close-coupling methods are used in the study of excitation in electron-molecule scattering. Two-state calculations for the state have been carried out by several groups using a variety of ab initio theoretical methods.^[7–12] Parker et al.^[13] reported four-state calculations by using the complex Kohn variational method (KV-4). The R-matrix method was performed by Branchett et al.^[14] at the seven-state level (RM-7). Machado et al.^[15] carried out the four-state calculations by using the method of continued fractions (MCF-4). More recently, the five-state Schwinger multichannel method (SMC-5) study was performed by da Costa et al.^[16]

Momentum-space methods are attractive from two points of view. First, differential cross sections are expressed in terms of the initial and final electron momenta so that the amplitudes involved in the calculation are directly related to the experiment. Second, the electron-molecule system has a single center in momentum space, whereas a tractable coordinate-space representation is multi-centered.^[17] The momentum-space optical method has been applied to elastic electron scattering from molecules.^[18–21] Recently, we developed a multichannel version of this method, and applied it to the calculations of the cross section for excitation in H₂ at the two-state close-coupling level of approximation.^[12] Our momentum-space multichannel optical method (MCO) computational code has now been extended to also account for multichannel interaction among excited states.

The long-range dipole coupling between states of the same spin is stronger than coupling between the singlet and the triplet. It is essential to include dipole coupling in the excited states manifold in order to achieve meaningful excitation cross sections for excitation from the ground state. We have performed calculations on excitation of the first three triplet excited states of ,, and . Comparison of DCSs for electronic excitation to the state of present four-state calculations with previous two-state data reveals how coupling between electronic excited states affects the differential cross sections in detail.

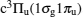
The unobserved channels have an effect on the observed channels. Real excitation of the unobserved channels is known as absorption. It removes flux from the observed channels. Virtual excitation of the unobserved channels is referred to as polarization of the target. In this study, a complex, equivalent-local and ab initio optical potential is used to treat the polarization effect and absorption by ionization continuum. The polarization potential contributes significantly to the scattering problem, particularly for forward scattering at intermediate energies.

In this paper, we report differential cross sections for the electron impact excitation of H₂ molecules. Our study includes the ,, and electronic transitions for impact energies 20 eV and 30 eV at the intermediate energies region where all four channels are open.

The momentum-space multichannel optical method is a multichannel version of the original momentum-space optical method.^[18] Details of the formulation have been given elsewhere,^[12,17] and here we will only present the basic aspects of the theory.

The T-matrix element for scattering from the initial channel |0k〉 to the excited channel |ik′〉 is calculated by solving the following momentum-space Lippmann–Schwinger equations:

The space of target states has been split into two parts. The P-space consists of a finite discrete set of channels. The Q-space is the continuum. The complex polarization potential element is written as

We make the following partial-wave expansion of the potential matrix elements.

It is a set of coupled integral equations, which is solved by matrix inversion after representing the q integration by a quadrature rule.^[17]

In practice as L increases the off-diagonal potential matrix elements decrease and become negligible after a value L₀. For L ≤ L₀ the corresponding set of coupled equations is solved fully. For L > L₀ the potential is essentially spherical and uncoupled integral equations are solved for each L.

The molecular orbital ψ_j is represented by a linear combination of atomic orbitals centered at the nuclear sites R_n. In the present calculation we use s and p orbitals, expressing the p orbitals in the Cartesian representation.

For target molecules in the gas phase, we assume random initial orientations and treat rotational excitation as an adiabatic process. This is equivalent to averaging the differential cross section over molecular orientations. Following the work of Gallup,^[22] we transform our entrance and exit channel momenta k₀ and k_i, which are expressed in the body-fixed frame, into momenta p₀ and p_i in the space-fixed (laboratory) frame. The transformation is affected by the rotation matrices,

The differential cross section is

Our calculations are performed within the framework of fixed-nuclei and Frank-Condon approximations at the equilibrium internuclear distance of 1.4 a₀. The wave functions of the target states ,,, and , consist of single-configuration wave functions in which the molecular orbitals are expanded in the Gaussian basis. The excitation energies for the transitions leading to the ,, and c³Π_u states are 9.98, 11.79, and 11.76 eV, respectively, which have been adopted from the relevant literatures.^[16,23] Coupling between partial waves is observed to become negligible beyond L = 8. On-diagonal matrix elements are included up to L = 30.

The differential cross section is the most sensitive test for theoretical models. The results for electronic excitation out of ground state into the higher levels at incident energies of 20 eV and 30 eV are shown in Figs. 1–6 separately and are compared with the latest experimental measurement^[4–6] and results from various theoretical models.^[14–16]

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Differential cross section for excitation of the state of H2 at the incident energy 20 eV. Theoretical work: Full curve, present; Dash, MCO-2;[12] Dot, RM-7;[14] Dash dot, MCF-4;[15] Dash–dot dot, SMC-5.[16] Experimental: full squares, Khakoo and Segura.[5]

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Differential cross section for excitation of the state of H2 at the incident energy 30 eV. Theoretical work: Full curve, present; Dash, MCO-2;[12] Dash dot, MCF-4;[15] Dash–dot dot, SMC-5.[16] Experimental: full triangle, Khahoo et al.[4]

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Differential cross section for excitation of the state of H2 at the incident energy 20 eV. Theoretical work: Full curve, present; Dot, RM-7;[14] Dash dot, MCF-4;[15] Dash–dot dot, SMC-5.[16] Experimental: bullet, Wrkich et al.[6]

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Differential cross section for excitation of the state of H2 at the incident energy 30 eV. Theoretical work: Full curve, present; Dash dot, MCF-4;[15] Dash–dot dot, SMC-5.[16] Experimental: bullet, Wrkich et al.[6]

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Differential cross section for excitation of the c3Πu state of H2 at the incident energy 20 eV. Theoretical work: Full curve, present; Dot, RM-7;[14] Dash dot, MCF-4;[15] Dash–dot dot, SMC-5.[16] Experimental: bullet, Wrkich et al.[6]

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Differential cross section for excitation of the c3Πu state of H2 at the incident energy 30 eV. Theoretical work: Full curve, present; Dash dot, MCF-4;[15] Dash–dot dot, SMC-5.[16] Experimental: bullet, Wrkich et al.[6]

Figures 1 and 2 show our differential cross sections for the transition at incident energies of 20 eV and 30 eV along with the measurements from Khakoo and Segura^[5] and Khakoo et al.,^[4] respectively. The calculations of RM-7,^[14] MCF-4,^[15] and SMC-5^[16] are also included. To investigate the effect of dipole coupling among the excited states, we also exhibit the previous two-state multichannel optical calculations (MCO-2).^[12] In the present four-state calculation, couplings between triplet electronic excited states are dipole allowed, which are expected to affect the result. For both of the incident energies, the small angle results show significant improvement towards the experimental data in comparison with the two-state calculations of MCO-2.^[12] Our calculated results and those of da Costa et al.^[16] (SMC-5) agree well with the experimental data^[4,5] at forward scattering angles, but underestimate the measurements from 90° to around 120°. Significantly differences can be seen at large angles, where our MCO-4 DCSs lie between those of the RM-7^[14] and the MCF-4^[15] at 20 eV. For the incident energy of 30 eV, the present results show the same minimum position with experimental data at around 110°. The differences at backward scattering angles are probably due to the differences in treatment of the polarization in these models.

In Figs. 3 and 4, we show differential cross sections for the transition from ground state to electronic state. Our DCSs at the incident energies of 20 eV and 30 eV are compared with those of RM-7,^[14] MCF-4,^[15] and SMC-5.^[16] The experimental data from Wrkich et al.^[6] are also included. For the incident energy of 20 eV the agreement of our calculated cross sections respect the experimental data from Wrkich et al.^[6] For small scattering angles our result is more forward peaked than the experimental data, but smaller than those of RM-7,^[14] and MCF-4.^[15] At 30 eV, the DCSs results obtained by the MCF-4^[15] calculations are better compared with measurements from Wrkich et al.^[6] At this energy the present calculations overestimate the experimental data, but agree well with the SMC-5^[16] results.

Differential cross sections for the electronic transition are presented in Figs. 5 and 6 and compared with experimental data from Wrkich et al.^[6] Other theoretical calculations of RM-7,^[14] MCF-4,^[15] and SMC-5^[16] are also included. As can be seen in Fig. 5, our results are in excellent agreement with the experimental measurements from Wrkich et al.^[6] and theoretical results from RM-7.^[14] At 30 eV the present results slightly overestimate the cross sections for angles above 30° than the measured values from Wrkich et al.^[6]

In this paper, we have presented an application of the multichannel optical method in the study of the electronic excitation of H₂ molecules by electron impact. DCSs for transitions leading to the lowest three triplet states of the target are calculated in a four-state level of close-coupling approximation. The discrepancy between the present MCO-4 results and previous MCO-2 results reveals the importance of the inclusion of multichannel effects in the calculation. The agreement between our results and experimental measurements is encouraging. We are interested in applying the MCO method to studies of electron collisions with larger molecules.