In the past two decades, high-order harmonic generation (HHG) has been extensively studied as a powerful tool for generating isolated attosecond pulses (IAP)^[1–5] and a coherent soft x-rays source.^[6] The physical mechanism of the HHG is well established by the three step model:^[7–9] the electron is freed by tunneling through the barrier of the atomic potential, then the ionized electron is accelerated by the laser field and captures energy, finally it may be driven back to the parent ion, emitting high energy photons. Compared with HHG from atoms, the process of harmonic emission from the molecules is much more complicated because of the interferences of different cores and complex molecular structures.

The potential applications of HHG from molecules such as real-time observation, molecular orbital tomographic imaging and reconstruction have attracted a lot of attention.^[10–15] The effect of intramolecular interference was investigated theoretically in and H₂ molecules by numerical solution of the Schrödinger equation or S-matrix method.^[16–18] In 2005, Itatani et al.^[19] realized to control the high order harmonic generation process by changing the alignment of molecules, they also accomplished the highest occupied molecular orbital (HOMO) of the N₂ molecule. With the development of science and technology, a lot of efficient methods have been proposed to provide information about the dynamics of orbital and nuclear.^[20–22] Recently, Guo et al.^[23] predicted that the linear combination of the HOMO and the lower-lying orbital below the HOMO (HOMO-1) can enhance the intensity of the HHG of the N₂ molecule. Pan et al.^[24] generated an isolated 38 as pulse from the oriented molecule CO exposed to a combined field of a few-cycle chirped laser and a unipolar pulse. As we all know, when an atom is exposed to circularly polarized laser fields, the ionized electron can hardly return to the parent ion, which leads to low efficiency of HHG. Much effort has been made to further investigate this phenomenon.^[25–27] It has been shown that a supercontinuum can be obtained by combining a left circularly pulse and a right circularly pulse with a certain delay.^[28] Yuan et al.^[29] achieved a single circularly polarized attosecond pulse by an intense few cycle elliptically polarized laser pulse combined with a terahertz field. Mancuso et al.^[30] observed experimentally the three-dimensional (3D) photoelectron distributions by two-color circularly polarized laser fields, which validated the theoretical strong-field model of HHG.

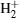
In this paper, we theoretically study the high-order harmonic generation of the N₂ molecule in the two-color circularly polarized laser fields by the strong-field Lewenstein model. We show that a continuous harmonic spectrum is obtained by the two-color circularly polarized laser fields alone, and in the addition of a static field to the x direction, the quantum path control is realized. We perform the time–frequency analysis and the semi-classical three-step model to show the underlying physical mechanism. As a result, an isolated attosecond pulse with a duration of 30 as can be generated directly by the superposition of the supercontinuum harmonics.

The strong-field Lewenstein model has been widely used to investigate the HHG of atoms and molecules.^[7,28,31,32] The transition amplitude for HHG can be calculated by the integral

We investigate the HHG of the N₂ molecule in the two-color circularly polarized laser fields, in which the HOMO constructed by the GAMESS-UK package^[33] is taken as the initial state. The transition amplitudes along the x and y direction can be expressed respectively as

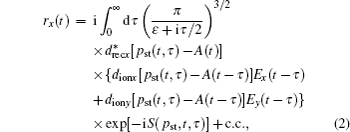
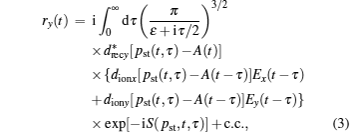
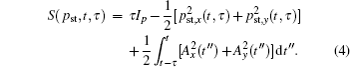
The harmonic spectrum intensity is proportional to the Fourier transformation of the time dependent dipole acceleration

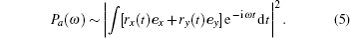
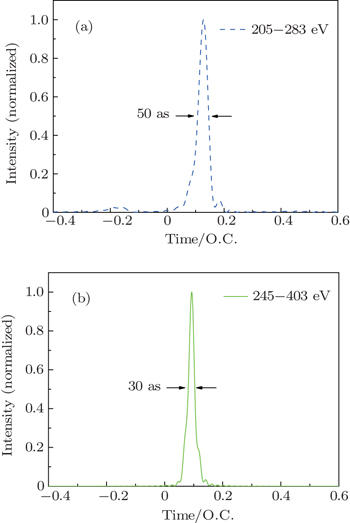
The temporal profile of an attosecond pulse can be obtained by superposing several harmonics in the x and y directions as follows:

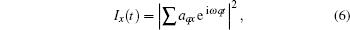
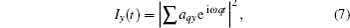
As we know, the electron ionized without an initial transverse velocity in the elliptical polarized laser field will miss the parent ion. A semi-classical three-step model with a proper initial transverse velocity was introduced, and the transverse displacement caused by the external field is compensated by an initial transverse velocity.^[34–36] Thus the semi-classical electron trajectories can be obtained as

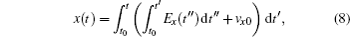
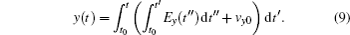
The initial velocities can be calculated as v_x0 = v_|| cos(α₀) + v_⊥ sin(α₀) and v_y0 = − v_|| sin(α₀) + v_⊥ cos(α₀), where v_|| and v_⊥ are the initial parallel velocity and transverse velocity, respectively. Since the electron leaves the molecule by tunneling, the initial velocity parallel to the ionizing field can be set as v_|| = 0. α₀ is the angle between the ionizing field vector and the coordinate axis at the ionization time t₀. The recombination time with a proper finite initial velocity will be obtained by calculating x(t) = 0, y(t) = 0.

We investigate the HHG process of the N₂ molecule in two-color circularly polarized laser fields and the HOMO is taken as the initial state as shown in Fig. 1. Atomic units are used throughout this paper unless otherwise stated. The electric fields of the left circularly polarized laser pulse E_l(t) and right circularly polarized laser pulse E_r(t) have the forms :

Fig. 1.

	Figure Option ViewDownloadNew Window
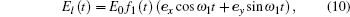
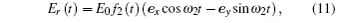
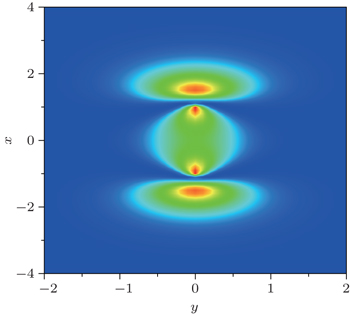	Fig. 1. The highest occupied molecular orbital (HOMO) of the N2 molecule using the GAMESS-UK package.

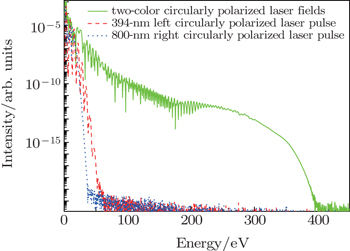
Figure 2(a) shows the electric field of the left circularly polarized laser pulse (green solid line), which shows that the laser field spirals contra-clockwise along the time positive axis. The ionized electrons circularly move away and hardly recombine with the parent core since the electric field force is always tangent along the circumference. The blue dashed line is the projection of left circularly polarized laser pulse on the x–y plane. In this paper, the time (the unit on the x axis) is shown in optical cycle (O.C.) of the left circularly polarized laser pulse (394 nm in wavelength).

Fig. 2.

Figure Option ViewDownloadNew Window

Fig. 2. (a) The electric field of the left circularly polarized laser pulse (green solid line) and the projection on the x–y plane (the blue dashed line); (b) The electric field of the right circularly polarized laser pulse (green solid line) and the projection on the x–y plane (the blue dashed line); (c) The electric field of the two-color circularly polarized laser fields (green solid line) and the projection on the x–y plane (the blue dashed line).

Figure 2(b) shows the electric field of the right circularly polarized laser pulse (green solid line) which circles clockwise spirally (800 nm in wavelength) along the time positive axis. The blue dashed line is the projection of right circularly polarized on the x–y plane.

Fig. 2(c) shows that the two-color circularly polarized laser field (the green solid line) changes are complicated and the projection on the x–y plane (the blue short dotted line) takes the shape of three-lobed distribution. It is clear to see that the electric field amplitude appears three peak values per laser cycle, which means that the ionized electrons can be driven back to the parent ion three times per laser cycle, each time at a different angle.

Figure 3 shows the harmonic spectra of the N₂ molecule generated by the left circularly polarized laser pulse, the right circularly polarized laser pulse and two-color circularly polarized laser fields. It is clear to see that there is almost no harmonic generated by the left or right circularly polarized laser pulse. While in the case of the two-color circularly polarized laser fields, we can see that the plateau of the spectra is extended and a continuous spectrum is generated from 250 eV to 363 eV with a bandwidth of about 113 eV.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Harmonic spectra of the N2 molecule generated in the left circularly polarized laser pulse (red dashed line), the right circularly polarized laser pulse (blue dotted line) and two-color circularly polarized laser fields (green solid line).

To explain the underlying mechanism of the extension of the HHG plateau, we demonstrate the emission time of the harmonics along the x and y directions in terms of the time–frequency analysis as shown in Figs. 4(a) and 4(b). It is shown that in both x and y directions there are five similar emission peaks, but the intensity of the emission peaks in the x direction is stronger than that in the y direction. Taking the emission time of the harmonics along the x direction for example, the maximum kinetic energy of the emission peak located around 0.24 O.C. reaches 363 eV, which corresponds to the cut-off energy of the spectrum. There is only one peak which makes a major contribution to the spectrum above 213 eV and the intensity of the short quantum path is much stronger than that of the long path. The destructive interference is weak, which leads to a continuous spectrum. The other emission peaks make a comparable contribution to the harmonics below 213 eV, which results in modulation structures in the lower harmonic energy region. All the discussions above are in good agreement with the results shown in Fig. 3 (see the green solid line).

Fig. 4.

	Figure Option ViewDownloadNew Window
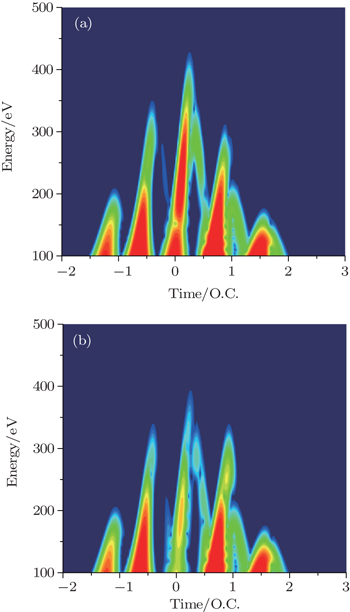	Fig. 4. The time–frequency analysis of the HHG spectrum along (a) x direction and (b) y direction in the two-color circularly polarized laser fields.

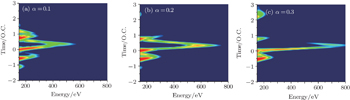
In order to extend the cut-off energy, we add a static electric field to the x direction and the expression is E_static = α E₀, where α is the static parameter. We investigate the HHG by the two-color circularly polarized laser fields combined with the static electric field for α = 0.1, α = 0.2, and α = 0.3. Figure 5 shows that in the lower energy region, the spectrums have little difference for three cases, but in the higher energy region, the plateau of the spectrum is dramatically extended with the increase of α. In the case of α = 0.3, the spectrum becomes very smooth, in which a supercontinnum appears with a bandwidth of 350 eV from 250 eV–600 eV and finally it reaches the cut-off at 730 eV.

Fig. 5.

	Figure Option ViewDownloadNew Window
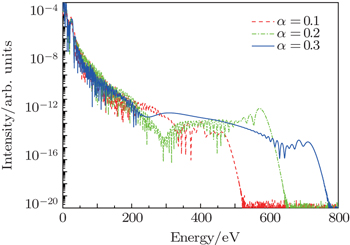	Fig. 5. Harmonic spectrums generated by the two-color circularly polarized laser fields combined with a static electric field for the static parameters α = 0.1, α = 0.2, and α = 0.3, respectively.

As the intensity of the harmonics for the x component is stronger by adding a static field in the x direction, we focus on the HHG process along the x direction. We demonstrate the corresponding time–frequency analysis of the spectrums along the x direction for three cases in Fig. 6(a), 6(b), and 6(c). One can see that only one emission peak is generated at about 0.4 O.C. in the higher energy region for three cases. With the increase of α the maximum energy of the emission peak is increased. For α = 0.3, the maximum energy of the emission peak reaches 730 eV and the long path is almost suppressed, which results in a supercontinumm spectrum in the higher energy region.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. The time–frequency analysis of harmonic spectrums along the x direction generated in two-color circularly polarized laser fields combined with a static field for (a) α = 0.1, (b) α = 0.2, and (c) α = 0.3.

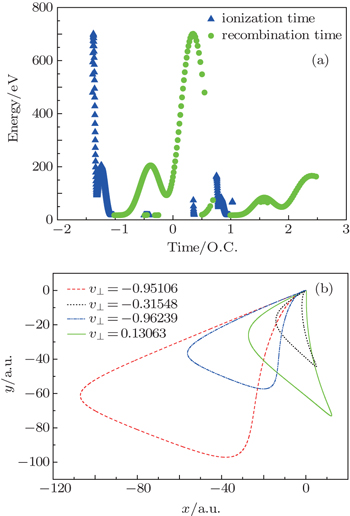
In order to further explain the mechanism of HHG in two-color circularly polarized laser fields combined with a static field for α = 0.3, we demonstrate the semi-classical three-step model with a finite initial transverse velocity, which is shown in Fig. 7(a). Under 230 eV, there are many emission peak bursts, which may lead to destructive interference structures among the spectrum in the lower energy region. The electrons ionized around −1.38 O.C. returned at about 0.33 O.C. with the maximum energy of 730 eV and the short trajectory makes a major contribution to the harmonics above 230 eV. Thus a supercontinuum spectrum can be obtained. These results are in good agreement with the analysis in Fig. 5 and Fig. 6(c).

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. (a) The dependence of the energy on the ionization (solid blue triangles) and emission times (solid green circles) in two-color circularly polarized laser fields combined with a static field for α = 0.3; (b) The electron trajectories with finite initial transverse velocities.

The electron trajectories around −1.35 O.C. with proper initial transverse velocities are shown in Fig. 7(b). It is shown that the electron can return to the parent ion with proper transverse velocities and thereby contribute to the generation of harmonics. Figure 7(b) also shows that the freed electron travels in triangular paths. The electric field of the two-color circularly polarized laser fields appear three peak values per laser cycle as shown in Fig. 2(c), which makes the freed electron may move along the triangular trajectories.

Figure 8 shows the attosecond pulse generated by the two-color circularly polarized laser fields (the blue dashed line shown in Fig. 8(a)) and the two-color circularly polarized laser fields combined with a static electric field for α = 0.3 (the green solid line shown in Fig. 8(b)). In the two-color circularly polarized laser fields, an IAP with the duration of 50 as is obtained by superposing several orders of the harmonics from 205 eV–283 eV, and with the addition of the static electric field, by superposing the harmonics from 245 eV–403 eV, the pulse width of the IAP’s can be reduced to 30 as.

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. The temporal profiles of the attosecond pulses generated by superposing several orders of the harmonics in (a) the two-color circularly polarized laser fields and (b) the combination of two-color circularly polarized laser fields and the static electric field for α = 0.3.

We investigated the HHG and the attosecond pulse generation of the N₂ molecule in two-color circularly polarized laser fields by the strong-field Lewenstein model. We show that a continuous spectrum of 113 eV can be generated by the two-color circularly polarized laser fields. By adding a static electric field to the x direction, the plateau of harmonic spectra is extended and a supercontinuum spectrum is generated. Both the time–frequency analysis and the semi-classical three-step model show that a dominant short quantum path is selected to contribute the harmonics in the higher energy region. By superposing several orders of harmonics in the combination of two-color circularly polarized laser fields and a static electric field, an isolated attosecond pulse with a bandwidth of 30 as is obtained directly.