Cite this Article
Yang Rong, Tang Bin, Gao Tao. Ab initio study on the electronic states and laser cooling of AlCl and AlBr. Chinese Physics B, 2016, 25(4): 043101  
Permissions
Ab initio study on the electronic states and laser cooling of AlCl and AlBr
Yang Rong1, 2, Tang Bin3, Gao Tao2, †,
College of Materials Science and Engineering, Chongqing Jiaotong University, Chongqing 400074, China
Institute of Atomic and Molecular Physics, Sichuan University, Chengdu 610065, China
Institute of Finance & Trade, Chongqing City Management College, Chongqing 401331, China

 

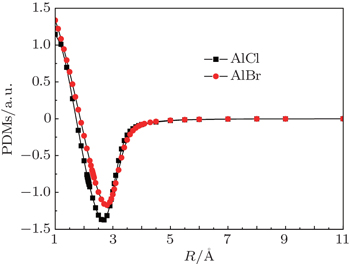
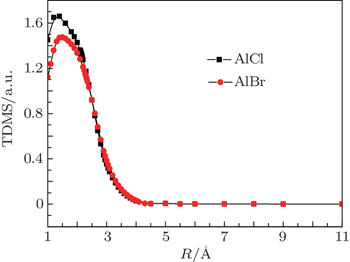
† Corresponding author. E-mail: gaotao@scu.edu.cn

Abstract
Abstract

We investigate whether AlCl and AlBr are promising candidates for laser cooling. We report new ab initio calculations on the ground state X1Σ+ and two low-lying states (A1Π and a3Π) of AlCl and AlBr. The calculated spectroscopic constants show good agreement with available theoretical and experimental results. We also obtain the permanent dipole moments (PDMs) curve at multi-reference configuration interaction (MRCI) level of theory. The transition properties of A1Π and a3Π states are predicted, including the transition dipole moments (TDMs), Franck–Condon factors (FCFs), radiative times and radiative width. The calculated radiative lifetimes are of the order of a nanosecond, implying that they are sufficiently short for rapid laser cooling. Both AlCl and AlBr have highly diagonally distributed FCFs which are crucial requirement for molecular laser cooling. The results demonstrate the feasibility of laser cooling AlCl and AlBr, and we propose laser cooling schemes for AlCl and AlBr.

PACS: 31.15.A–;37.10.Mn;87.80.Cc;
Keyword:AlCl;AlBr;laser cooling;
1. Introduction

Ultracold molecules offer a unique opportunity for studying chemical reactions at the quantum state level. Recently, the laser cooling of diatomic molecules has been demonstrated in the laboratory.[1–3] It is notable that molecule SrF1 has been directly cooled by Doppler and Sisyphus cooling for the first time. Later YO2 and CaF3 have also been experimentally cooled by laser cooling. It would be good to note that similar schemes have now been proposed for molecular ions (eg the molecular hydrogen ions[4] HD+). The researches on the laser cooling in our country are also motivated by all sorts of prospective applications.[5–7] Since there are more than 90 elements in the periodic table, it may form more than 4000 different diatomic molecules. Naturally the search for potential laser cooling candidates is getting people to pay attention. For laser cooling of a molecule, it is very difficult to keep a closed optical pumping cycle with repeated optical spontaneous emissions due to the molecule’s complex internal structure. SrF, YO, and CaF all demonstrate highly-diagonal Franck–Condon factors (FCFs) which suppress decays to unwanted sublevels. So in order to be a possible source for laser cooling, the molecule must meet the first criteria: highly-diagonal FCFs. The highly-diagonal FCFs would limit the number of lasers required to keep the molecule in a closed-loop cooling cycle. A second criteria is that rapid laser cooling calls for shorter lifetimes. SrF, YO, and CaF all have short lifetimes. The calculations of FCFs and lifetimes would help us to identify promising candidates for laser cooling theoretically. Thus, we use ab initio calculations to investigate the possibility of laser cooling AlCl and AlBr in this paper.

In 2004, a brief survey of laser cooling candidates was presented by Di Rosa.[8] The list of candidates included aluminum compounds. The laser cooling of the related diatomics AlH and AlF has been discussed in detail by Wells and Lane.[9] They identified AlH and AlF as suitable laser cooling candidates. Now we would like to choose the two molecules AlCl and AlBr, since they have large emission probability (thus high scattering rates), very low scattering probabilities into off-diagonal bands 0 → 1 and 0 → 2, the desirable 1Π ← 1Σ+ cycling transitions and extremely short excited state lifetimes.

Aluminum monohalides (AlCl and AlBr) are readily produced in the vapor phase by high temperature pyrolysis[10] and from chemiluminescent reactions[11] of Al atoms with the halogens. A high-resolution emission spectrum of AlCl at 20 μm was conducted by Hedderich et al.[12] They have found that the ground state X1Σ+ of AlCl possesses a deep potential. The previous experimental studies of electronic excited states for AlCl consisted mainly of absorption and emission spectra from the first singlet–singlet (i.e. A–X), triplet–triplet (b–a) and triplet–singlet (a–X) systems.[12–18] Theoretical calculations have also been performed for AlCl over the past several decades. For AlCl, the potential curves for the X1Σ+ and A1Π states, and A1Π vibrational lifetimes were given by Langhoff et al.[19] Brites et al.[20] obtained the lifetime of AlCl for the A1Π ν′ = 0 level of 5.9 ns. These authors all agreed that AlCl has highly-diagonal FCFs and short radiative lifetimes. Several experimental and theoretical studies of the AlBr molecule are also available. Bredohl et al.[21] have provided an extensive high-resolution band-by-band analysis of 28 bands of the A–X transition of AlBr. The A1Π –X1Σ+ transition of AlBr was recorded by Fleming et al.[22] using a Bruker IFS 120 HR Fourier transform spectrometer. Their results showed that the 0–0 band was the most intense and the Δν = 0 sequence dominated the observed spectrum. Recent theoretical calculations have been performed for 12 electronic states for AlBr by Hamade et al.[23] The radiative lifetime for the ν′ = 0 level of the A1Π state was computed by Langhoff et al.[19] to be about 8.5 ns for AlBr using averaged complete active space self-consistent field (CASSCF)[24,25] calculations.

As stated above, AlCl and AlBr have been researched systematically. Nevertheless, systematic studies of laser cooling of AlCl and AlBr are not available in the literature. So our work focuses on identifying whether AlCl and AlBr are possible candidates for laser cooling with ab initio calculations. Because AlCl and AlBr both possess 1Π ← 1Σ+ transition, the FCFs, transition dipole moments (TDMs), radiative lifetimes and radiative widths of the A1Π –X1Σ+ transtions of AlCl and AlBr are predicted. Also accurate determinations of the spectroscopic constants, potential energy curves (PECs) and permanent dipole moments (PDMs) of the X1Σ+ and A1Π states of AlCl and AlBr have been given. Additionally, there is a low lying a3Π state between the A1Π and ground states for AlCl and AlBr. The PECs, spectroscopic constants of a3Π state, and the transition properties of the a3Π state to the ground state are also obtained. Finally, we briefly design laser cooling schemes for AlCl and AlBr.

The present paper is organized as follows. In Section 2 we give the details of our calculations. Section 3 presents the results and discussion, outlining laser cooling schemes for AlCl and AlBr. The conclusions are summarized in Section 4.

2. Computational method

All our ab initio calculations are performed using the MOLPRO package.[26] The ground state (X1Σ+) and two low-lying excited states (A1Π and a3Π) for AlCl and AlBr have been conducted with multi-reference configuration interaction (MRCI) plus Davidson corrections[27–29] which is based on CASSCF[24,25] wave functions. For AlBr, the scalar relativistic effects are taken into account using the Douglas–Kroll–Hess[30,31] transformation of the relativistic Hamiltonian. The spectroscopic constants (Re, De, we, weχe, Be, Te) are derived by using Le Roy’s LEVEL 8.0 program.[32] The PDMs and TDMs of AlCl and AlBr are evaluated by taking the expectation and transition values using the MRCI wave functions. Spin–orbit coupling is ignored in our calculations, since the principal transitions under investigation are singlet states.

In our calculations, the basis sets aug-cc-PVQZ[33] are used for Al and Cl. As for Br, we choose the small-core scalar relativistic effective core potential ECP10MDF[34] together with the corresponding valence basis sets.[35] Owing to the limitation of the MOLPRO software package, C2ν point group symmetry has been considered for AlCl and AlBr in all computations, which holds (a1, b1, b2, a2) irreducible representations. For AlCl, eight molecule obitals (MOs) are put into active space, including four a1, two b1, two b2 symmetry MOs (4220), which correspond to the 3s3p shells of the Al atom and 3s3p shells of the Cl atom. The active space of AlBr consists of eight MOs 4a1, 2b1, 2b2, 0a2 (4220) which correspond to Al 3s3p and Br 4s4p.

3. Results
3.1. PECs and spectroscopic constants

Figure 1 shows the PECs of the ground state (X1Σ+) and two low-lying excited states (A1Π and a3Π) of AlCl and AlBr obtained at the MRCI level of theory. We summarize the corresponding spectroscopic constants in Table 1. Previous experimental and theoretical data are listed together.

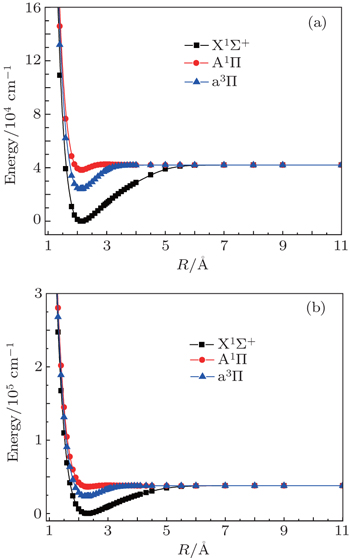Fig. 1. Potential energy curves of the first three electronic states of AlCl (a) and AlBr (b) at the MRCI level of theory.
Table 1.

Calculated spectroscopic constants of X1Σ+, A1Π, and a3Π states of AlCl and AlBr at the MRCI level of theory.

.

For AlCl, our results are close to the experimental data. The percentage error in Re, we, and weχe are 0.70%, 0.69%, and 5.80% for the ground state X1Σ+ of AlCl. Findings for the excited state a3Π of AlCl are similar; the percentage error in Re, we, and weχe are 0.57%, 0.19%, and 19.72% compared with the experimental data.[17] Although the deviation of the weχe seems to be a little large, our calculated values are closer to the experimental data[17,35] than the theoretical results obtained by Brites et al.[20] The percentage error in weχe calculated by Brites et al.[20] are 212.56% and 76.09% for the X1Σ+ and a3Π states of AlCl. The computed ground state dissociation energy De of 5.22 eV compares well with the experimental value of (5.25±0.01) eV.[14,36] Our calculated Te result is only 49 cm−1 larger than the observed data[37] for the A1Π state of AlCl.

We turn now to the discussion of AlBr. Our calculated spectroscopic constants of AlBr are also close to the experimental values, compared with previous theoretical data obtained by Langhoff et al.[19] The calculated Re, we, and Be for X1Σ+ state of AlBr are 2.306 Å, 378.72 cm−1 and 0.1577 cm−1 respectively, which are in good agreement with the experimental data 2.295 Å, 378.11 cm−1, and 0.1592 cm−1. For the A1Π state of AlBr, the percentage error in Te, Re, and we are 1.50%, 0.13%, and 6.22% compared with the experimental data,[22] and for the a3Π states of AlBr, the percentage error in Te, we, and weχe are 1.98%, 0.20%, and 0.29%.

Overall, our computed spectroscopic constants agree well with the experimental data as well as other available theoretical results. We expect that our methods are accurate for the two molecules.

3.2. PDMs and TDMs

Figures 2 and 3 show the PDMs of the X1Σ+ and A1Π states of AlCl and AlBr as functions of the internuclear distance at the MRCI level, respectively. A study of Fig. 2 reveals that at short bond lengths the dipole of each molecule possesses an essentially linear dependence with the increase of the internuclear distance indicative of an ionic molecule. The absolute magnitude reaches a maximum (AlCl: −4.11 a.u. (the unit a.u. is short for atomic unit), AlBr: −3.52 a.u.) and drops thereafter. The dipole falls to zero at around 7 Å for both molecules. As shown in Fig. 3, the PDMs of the A1Π state demonstrate similar behavior as the PDMs of the X1Σ+ state. The peaks of the PDMs are −1.38 a.u. and −1.17 a.u. for AlCl and AlBr, respectively.

Fig. 2. PDMs of X1Σ+ state at the MRCI level for AlCl and AlBr.
Fig. 3. PDMs of A1Π state at the MRCI level for AlCl and AlBr.

The relationship between the TDMs of the A1Π –X1Σ+ transitions and the internuclear distance is depicted in Fig. 4. For AlCl and AlBr, the TDMs show similar behavior. The magnitude gradually increases as internuclear distance R increases, reaches a maximum (AlCl: 1.66 a.u., AlBr: 1.47 a.u.), and drops thereafter.

Fig. 4. TDMs for the transitions from the A1Π state to the X1Σ+ state at MRCI level of AlCl and AlBr.
3.3. Radiative lifetime and radiative width

Rapid laser cooling requires sufficiently short lifetimes, which can provide a significant rate (105 s−1–108 s−1) of optical cycling. The radiative lifetimes and radiative width for the transitions from the A1Π state to the ground state X1Σ+ are collected in Table 2. The other theoretical results[19] are also listed in Table 2 for comparison. Table 2 shows that in all cases the lifetimes increase slowly with the vibrational quantum number. For AlCl, our computed lifetime for the A1Π ν′ = 0 level of 5.04 ns is close to the experimental value of (6.4±2.5) ns determined by Rogowski and Fontijn.[39] For AlBr, our value for the ν′ = 0 level of 8.53 ns also agrees with the theoretical value of 8.5 ns estimated by Langhoff et al.[19]

Table 2.

Estimated radiative lifetimes (in unit ns) and radiative width (in unit cm−1) (in italics) for A1Π → X1Σ+ transitions. Theoretical values obtained by Langhoff et al. in brackets.

.

The radiative lifetimes of the A1Π (ν′) vibrational states are computed to be 5.04 ns–5.76 ns and 8.53 ns–10.83 ns for the first five vibrational levels (ν′ = 0–4) of AlCl and AlBr. So these lifetimes are sufficiently short that AlCl and AlBr meet the criteria as suitable laser cooling candidates. Taking the ν′ = 0 level as an example, the line strengths (Einstein A coefficients) of the A1Π (ν′ = 0) vibrational states for AlCl and AlBr are 1.98×108 s−1 and 1.17×108 s−1, giving lifetimes of 5.04 ns and 8.53 ns (about 1/5 and 2/5 that of the transition in SrF). The radiative widths of the a3Π and A1Π vibrational states are predicted in Table 2 for AlCl and AlBr. In all cases, the radiative widths show a slight decrease with increasing ν′.

3.4. FCFs and proposed laser cooling scheme

The calculated FCFs in AlCl for the transition A1Π → X1Σ+ are tabulated in Table 3. Langhoff et al.[19] did not give FCFs for A1Π → X1Σ+ transition in AlCl. But Einstein coefficients (A) were given (A00 = 1.933×108 s−1, A11 = 1.891×108 s−1, A22 = 1.832×108 s−1, A33 = 1.735×108 s−1) by them. Our calculated Einstein coefficients are the following: A00 = 1.979×108 s−1, A11 = 1.921×108 s−1, A22 = 1.841×108 s−1 and A33 = 1.716×108 s−1. Thus, our results can be compared with the results obtained by Langhoff et al.[19] Of course, our calculated FCFs need to be confirmed by later experimental data. It can be seen that the determined FCFs of AlCl are highly diagonally (f00 = 0.9993, f11 = 0.9960, f22 = 0.9819, f33 = 0.9419). Highly-diagonal FCFs are desirable for laser cooling. The calculated ν′ = 0 → ν = 0 FCF (f00) of 0.9993 (Table 3), is larger than that predicted in SrF (f00 = 0.98), thus it is sufficiently large to be potentially viable for cooling. On the basis of the calculated FCFs, we propose a two color laser cooling scheme. The main cooling transition is the transition A1Π (ν′ = 0) ← X1Σ+ (ν = 0) using wavelength λ00 = 261.2 nm (Fig. 5(a)); the corresponding experimental value[37] is 261.5 nm. Because there is a non-negligible probability of decay to the X1Σ+ (ν = 2) state (≈ 0.07%), a repumping laser can be tied to the ν′ = 1 ← ν = 2 transition with λ21 = 258.6 nm. Decays to the X1Σ+ (ν = 3) state occur with probability ≈ 10−6. Using the repump should result in Nscat = 1/f03 + > 106 photons scattered before higher vibrational levels are populated. The required cooling wavelength is deep into the UVC range (UVC: 280–190 nm), where it is hard to produce continuous wave laser radiation. However, a frequency tripled Ti: sapphire laser should be capable of generating useful quantities of light at the wavelength (261.2 nm). It is also important to note that there is a low lying a3Π state between the two states (A1Π and X1Σ+) for AlCl. The intervening a3Π state could kill the cooling scheme based on the transition A1Π ← X1Σ+, if the a3Π ← A1Π transition depopulates the excited state. So far there has been no experimental observation of the a3Π ← A1Π transition. The rate for the A1Π → a3Π transition should be very small. Also we have computed the FCFs for the a3Π → X1Σ+ transition, in order to see whether the a3Π → X1Σ+ transition is another option for laser cooling.

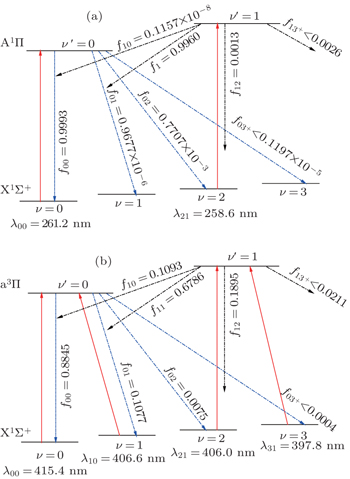Fig. 5. Proposed laser cooling schemes for AlCl using the (a) A1Π (ν′) ← X1Σ+ (ν) and (b) a3Π (ν′) ← X1Σ+ (ν) transitions with the calculated FCFs fν′ν and wavelength λν′ν.
Table 3.

The calculated FCFs fν′ν of AlCl for A1Π (ν′) → X1Σ+ (ν) and a3Π (ν′) → X1Σ+ (ν) transitions. Characteristic base 10 given parenthetically.

.

Table 3 shows that the FCFs for the a3Π → X1Σ+ transition are still highly diagonal. Thus, a four colour laser cooling scheme for AlCl using the a3Π → X1Σ+ transition is shown in Fig. 5(b). The main cycling laser drives the a3Π (ν′ = 0) ← X1Σ+ (ν = 0) transition at length 415.4 nm (visible violet region, the corresponding experimental value is 407.36 nm[18]). The a3Π (ν′ = 0) ← X1Σ+ (ν = 1) transition as the first vibrational repump and the a3Π (ν′ = 1) ← X1Σ+ (ν = 2) transition for the second repump are required to reclaim molecules falling from ν′ = 0 to ν = 1 (FCF = 0.1077) and ν′ = 1 to ν = 2 (FCF = 0.1895). Owing to the non-negligible a3Π (ν′ = 1) to X1Σ+ (ν = 3) transition (FCF = 0.0211), a third repumping laser may be required on that transition. The relatively long lifetimes of the a3Π state can be exploited to reach a much lower Doppler temperature than possible on the A1Π ← X1Σ+ transition. Considering that the 0–0 band of the a3Π → X1Σ+ transition of AlCl at 407.36 nm has been observed by Saksena et al.,[18] AlCl may first be cooled on the strong A1Π ← X1Σ+ transition, then be further cooled on the weak a3Π ← X1Σ+ transition. This is similar to the laser cooling of alkaline earth atoms.

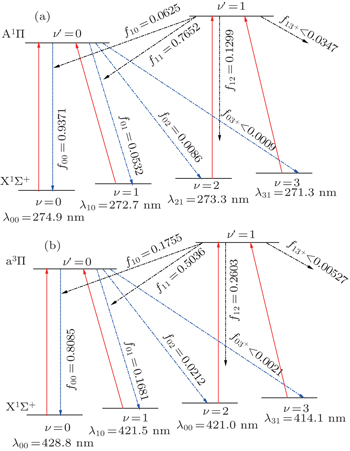Turning to AlBr, the FCFs follow the same trend as that of AlCl (see Table 4). Although there are currently no experimental or theoretical data for FCFs of AlBr for comparison, our calculated wavelengths in Table 4 are close to the corresponding experimental values. The electronic spectrum of A1Π –X1Σ+ and a3Π –X1Σ+ transitions were observed near 280 nm[38] and 420 nm.[38] As in AlCl, there is an a3Π state between A1Π and X1Σ+ states for AlBr. For simplicity, here we only propose laser cooling schemes of AlBr in Fig. 6.

Fig. 6. Proposed laser cooling schemes for AlBr using the (a) A1Π (ν′) ← X1Σ+ (ν) and (b) a3Π (ν′)← X1Σ+ (ν) transitions with the calculated FCFs fν′ν and wavelength λν′ν.
Table 4.

The calculated FCFs fν′ν and wavelength λν′ν of AlBr for A1Π (ν′) → X1Σ+ (ν) and a3Π (ν′) → X1Σ+ (ν) transitions. Characteristic base 10 given parenthetically.

.

On the whole, we have identified AlCl and AlBr as promising laser cooling candidates. Compared with AlBr (f00 = 0.9371), AlCl (f00 = 0.9993) is more promising. Because of the hyperfine structure present in Al diatomics, sub- Doppler sisyphus cooling can take place in AlCl and AlBr just like alkali atoms. For AlCl and AlBr, the A1Π ← X1Σ+ transition may be followed by the weak a3Π ← X1Σ+ transition. The recoil temperature (Trecoil = (h/λ)2/2mkB) is the temperature limitation. AlCl and AlBr have greater mass and cooling wavelengths of lower energy (AlCl: 415.4 nm; AlBr: 428.8 nm) than AlF investigated by Wells and Lane.[9] So the recoil temperature for AlCl and AlBr will be smaller than AlF.

4. Conclusions

We have calculated the X1Σ+, A1Π, and a3Π states of AlCl and AlBr in order to explore the possibility of laser cooling these molecules. First, we investigated the PECs and spectroscopic constants (Re, De, we, weχe, Be, Te). The calculated spectroscopic constants are in good agreement with previous theoretical and experimental data. Second, PDMs and TDMs have been calculated for the X1Σ+ and A1Π states. Finally, we obtained FCFs, radiative lifetimes and radiative widths. The results demonstrate that both molecules have highly diagonally distributed FCFs and short lifetimes. It means that AlCl and AlBr meet the criteria as promising candidates for direct laser cooling. Additionally, we have briefly designed laser cooling schemes for AlCl and AlBr. Since the a3Π → X1Σ+ transition is also strongly diagonal and the lifetimes of the excited a3Π state are relatively long, the A1Π ← X1Σ+ transition may be followed by the weak a3Π ← X1Σ+ transition to obtain a lower Doppler temperature.

Reference
1Shuman E SBarry J FDeMille D 2010 Nature 467 820
2Hummon M TYeo MStuhl B KCollopy A LXia YYe J 2013 Phys. Rev. Lett. 110 143001
3Zhelyazkova VCournol AWall T EMatsushima AHudson J JHinds E ATarbutt M RSauer B E 2014 Phys. Rev. 89 053416
4Shen JBorodin AHansen MSchiller S 2012 Phys. Rev. 85 032519
5Wang Y Z2011Physics40421(in Chinese)
6Xu ZDang W RWang Y Z2008Physics37708(in Chinese)
7Zhou S YLong QZhou S YFu H XWang Y Z2002Physics31481(in Chinese)
8Di Rosa M D 2014 Eur. Phys. J. D 31 395
9Wells NLane I C 2011 Phys. Chem. Chem. Phys. 13 19018
10Dyke J MKirby CMorris AGravenor B W JKlein RRosrnus P 1984 Chem. Phys. 88 289
11Rosenwaks S 1976 J. Chem. Phys. 65 3668
12Hedderich H GDulick MBernath P F 1993 J. Chem. Phys. 99 8363
13Mahanti P C 1934 Z. Phys. 88 550
14Hildenbrand D LTheard L P 1969 J. Chem. Phys. 50 5350
15Mahieu EDubois IBredohl H 1989 J. Mol. Spectrosc. 134 317
16Mahieu EDubois IBredohl H 1989 J. Mol. Spectrosc. 138 264
17Sharma D 1951 Astrophys. 113 210
18Saksena M DDixit V SSingh M 1998 J. Mol. Spectrosc. 187 1
19Langhoff S RBauschlicher C WJrTaylor P R 1988 J. Chem. Phys. 88 5715
20Brites VHammout‘ene DHochlaf M 2008 J. Phys. Chem. 112 13419
21Bredohl HDubois IMahieu EMellen F 1991 J. Mol. Spectrosc. 145 12
22Fleming P EMathews C W 1996 J. Mol. Spectrosc. 175 31
23Hamade YTaher FMonteil Y 2010 Int. J. Quantum Chem. 110 1030
24Werner H JKnowles P J 1985 J. Chem. Phys. 82 5053
25Knowles P JWerner H J 1985 Chem. Phys. Lett. 115 259
26Werner H JKnowles P JManby F RSchutz MCelani PKnizia GKorona TLindh RMitrushenkov ARauhut Get al.2010MolproBirminghamUniversity of Birmingham ALsee http://www.molpro.net.
27Werner H JKnowles P J 1988 J. Chem. Phys. 89 5803
28Knowles P JWerner H J 1988 Chem. Phys. Lett. 145 514
29Langhoff S RDavidson E R 1974 Int. J. Quantum Chem. 8 61
30Douglas NKroll N M 1974 Ann. Phys. 82 89
31Hess B A 1986 Phys. Rev. 33 3742
32Le Roy R J2007LEVEL 8.0: A Computer Program for Solving the Radial Schrödinger Equation for Bound and Quasibound Levels, CPRR-661WaterlooUniversity of Waterloo, ON, Canada
33Woon D EDunning T HJr 1993 J. Chem. Phys. 98 1358
34Peterson K AFiggen DGoll EStoll HDolg M 2003 J. Chem. Phys. 119 11113
35Wyse F CGordy W 1972 J. Chem. Phys. 56 2130
36Ram R SRai S BUpadhya K NRai D K 1982 Phys. Scr. 26 383
37Huber K PHerzberg G1979Molecular Spectra and Molecular StructureNew YorkVan Nostrand Reinhold
38Griffith W BJ RMathews C W 1984 J. Mol. Spectrosc. 104 347
39Rogowski D FFontijn A 1987 Chem. Phys. Lett. 137 219