Cite this Article
Zhang Hai-Long, Zhou Chun, Shi Jian-Hong, Bao Wan-Su. Fidelity between Gaussian mixed states with quantum state quadrature variances. Chinese Physics B, 2016, 25(4): 040304  
Permissions
Fidelity between Gaussian mixed states with quantum state quadrature variances
Zhang Hai-Long1, 2, 3, †, , Zhou Chun1, 2, Shi Jian-Hong1, 2, Bao Wan-Su1, 2
Zhengzhou Information Science and Technology Institute, Zhengzhou 450004, China
Synergetic Innovation Center of Quantum Information and Quantum Physics, University of Science and Technology of China, Hefei 230026, China
Science and Technology on Information Assurance Laboratory, Beijing 100071, China

 

† Corresponding author. E-mail: zhhl049@126.com

Project supported by the National Basic Research Program of China (Grant No. 2013CB338002) and the Foundation of Science and Technology on Information Assurance Laboratory (Grant No. KJ-14-001).

Abstract
Abstract

In this paper, from the original definition of fidelity in a pure state, we first give a well-defined expansion fidelity between two Gaussian mixed states. It is related to the variances of output and input states in quantum information processing. It is convenient to quantify the quantum teleportation (quantum clone) experiment since the variances of the input (output) state are measurable. Furthermore, we also give a conclusion that the fidelity of a pure input state is smaller than the fidelity of a mixed input state in the same quantum information processing.

PACS: 03.67.Lx;03.67.Ac;
Keyword:fidelity;mixed state;quantum clone;quantum information processing;
1. Introduction

Recently, much attention has been devoted to investigating the use of continuous variable quantum information processing (CV-QIP). Continuous-spectrum quantum variables may be easier to manipulate than discrete quantum bits in order to perform various quantum information processes. For the case of Gaussian state of light, e.g., squeezed coherent beams,[1] it can be created by means of linear optical circuits and homodyne detection, which can be used to perform quantum teleportation,[2] quantum error correction,[3] and even a quantum nonlocality test. The similarity or distinguishability of CV quantum states is an important resource in quantum information processing and there are several measures widely used to characterize it, such as trace distance[4] and fidelity.[5–8]

The fidelity is an average value which is often used in CV-QIP.[8] The experiments with a coherent state input have been performed by assuming that the input is a pure state. For such a state, there have been a lot of studies of fidelity as a success criterion, and its value and the classical limit are well understood.[9–14]

In theory, the fidelity between any two mixed states is[6,7]

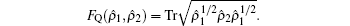
However it is not easy to compute the square root of a density operator. Moreover the input state cannot be always pure but is mixed due to some inevitable losses and imperfection in real experiments, so it is difficult to quantify the similarity between mixed states in experiments. In experiments there is a need for other quantities, which are easier to compute and measure, and the fidelity for CV teleportation of a mixed state input has not been investigated very much so far.

In this paper, based on the original definition of fidelity, we first give a well-defined universal fidelity between two Gaussian mixed states. It is related to the variances of output and input states in quantum information processing. We can use it to quantify the quantum teleportation (quantum clone) experiment conveniently since the variances of input (output) state are measurable. Furthermore, we also give a conclusion that the fidelity of a pure input state is smaller than the fidelity of a mixed input state in the same quantum information processing, which means it is harder to preserve the quantum character of a pure state than a mixed state.

2. Fidelity between Gaussian mixed states

The fidelity for a pure input state,[8]

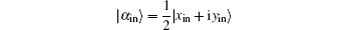
with xin (yin) the expectation value of the amplitude (phase) quadrature, is defined by Schumacher F = 〈αin|ρout|αin〉, where ρout is the density operator of the output state, and the fidelity is equivalently expressed with the Wigner function[15] by

where Win(α) and Wout(α) are the Wigner functions of the input and output states, respectively.

In this paper the states we considered are Gaussian states, which are at the heart of quantum information processing with continuous variables. They can also be generated and manipulated experimentally in a variety of physical systems, ranging from light fields to atomic ensembles.

A state of a continuous variable system is called Gaussian if its Wigner function, or equivalently its characteristic function, is Gaussian. If the input is a Gaussian state, we can denote the input state Wigner function as

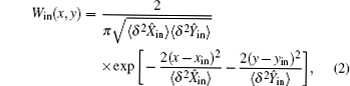
where xin and yin are the displacement (also named the expectation value in theory) of the input state in the phase space and 〈δ2X̂in〉 and 〈δ2Ŷin〉 are the quadrature component variances of the input state.

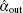
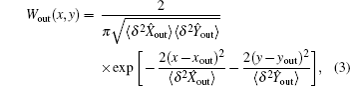
In the CV-QIP, the Gaussian character of the input state does not need be altered. Even when a Gaussian state suffers from some losses in the CV-QIP and becomes a mixed state, the state is just transformed into another Gaussian state. So we can also denote the Wigner function as

where xout (yout) and 〈δ2X̂out〉 (〈δ2Ŷout〉) have the same meaning with Eq. (2).

If the input is prepared in a pure state, the fidelity is calculated[6,7] by Eq. (1),

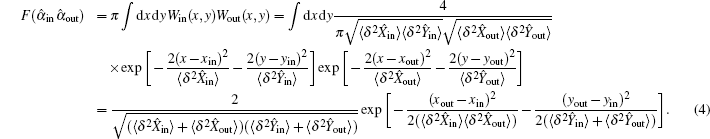
The displacement xin (yin) of an input state can be easily reconstructed at the output station by setting the gains of classical channels to unity, i.e., xout = xin, yout = yin, where the fidelity is peaked,

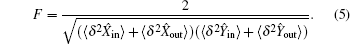
It only depends on the variances of the input state and output state, which are just what we measured in the CV-QIP experiment.

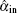
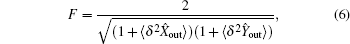
When the input state is a pure coherent state, it means 〈δ2X̂in〉 = 〈δ2Ŷin〉 = 1, equation (5) changes as

Furusawa et al.[14] used this expression to investigate the fidelity of continuous-variable quantum teleportation for a pure coherent state.

However, the input state cannot always be a pure state but is a mixed state due to some inevitable losses and imperfection in real experiments. For example, squeezed states used in successful experiments of quantum teleportation or the generation of entanglement are commonly generated by using an optical parametric oscillator[14,18–22] or a Kerr medium.[23] In these experiments, each squeezed state suffers from some inevitable losses, mainly in its generation process, having excess noise in the antisqueezing component. Such squeezed states are not pure, but mixed states. So we cannot directly qualify the similarity between the input and output state.

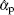
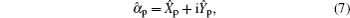
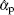
Here we can assume the ideal input is a Gaussian pure state. The subscript ‘p’ means pure. Without loss of generality, the ideal input state can be expressed as

which is expressed in terms of the amplitude X̂p and the phase Ŷp quadrature with the canonical commutation relation [X̂p,X̂p] = 2i, and 〈δ2Âp〉 are the quadrature component variances with  = X̂ = Ŷ. xp and yp are the expectation values of the X̂p and Ŷp. Since is a pure state, we have 〈δ2X̂p〉·〈δ2Ŷp〉 = 1.

Due to some inevitable noise coupled in the ideal input state in the state preparation process, the ideal input state is transformed into the real prepared input state . It is usually a mixed state. The prepared input state can also be expressed as

Note that 〈δ2Âin〉 are the quadrature variances with  = X̂ or Ŷ. xin and yin are the expectation values of X̂in and Ŷin. Since the prepared input is a mixed state, we have

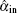
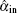
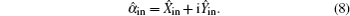
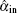
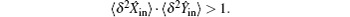
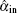
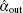
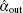
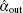
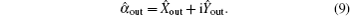
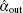
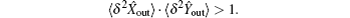
Due to the no-cloning theorem, the state transport process inevitably induces noise in comparison with the input state . The outputs of the state transport process are also a Gaussian mixed state. In fact, the additional noise of the output state is a penalty during the state transport process. The output state can also be expressed as

Note that xout and yout are the expectation values of X̂out and Ŷout. Since the output state is a mixed state, we have

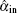
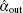
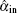
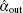
Since the prepared input state and the output state are both mixed states, how can we qualify the similarity between and .

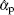
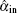
First, because the ideal input is a pure state, we can calculate the fidelity between and by Eq. (4),

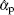
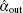
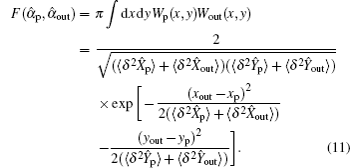
Similarly, we can also calculate the fidelity between and

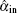
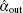
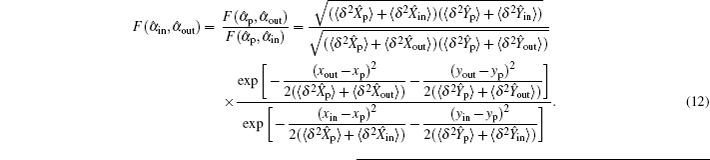
A well-defined fidelity must qualify the similarity between quantum states. In mathematics, the value of the fidelity must belong to [0,1]. So the fidelity between mixed states and is defined as

Considering two ideal cases, firstly, when

and

the fidelity

secondly, when

and

the fidelity

So it is a well-defined fidelity which can qualify the similarity between mixed states. It can be seen that the fidelity depends not only on the variances of two states but also on the displacement subtraction. In the quantum clone (quantum teleportation) experiment,[18–20,24] the displacement xin (yin) of an input state can be easily reconstructed at the output station by setting the gains of classical channels to unity, i.e., xout = xin, yout = yin. Since is a hypothetical input, we can assume xp = xin = xout, yp = yin = yout, and the fidelity is strongly peaked and changed into

There is a similar idea of Schrödinger’s-cat states in quantum teleportation by Furusawa.[24] Considering two ideal cases, first, when

and

the fidelity F = 1; second, when 〈δ2X̂out〉 ≫ 〈δ2X̂in〉 and 〈δ2Ŷout〉 ≫ 〈δ2Ŷin〉, the fidelity F = 0. It only depends on the variances of the input state and output state, which are just what we measured in the experiment. It is very useful to qualify the Gaussian state quantum teleportation (quantum clone) experiment.

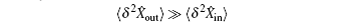
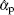
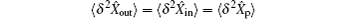
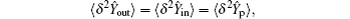
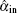
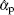
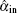
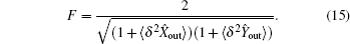
When the prepared input state is a pure state, its means , equation (13) agrees with Eq. (5). When the ideal state is a coherent state, i.e., 〈δ2X̂p〉 = 〈δ2Ŷp〉 = 1, equation (13) is changed into

However, all experiments[14,18–20,25] with a coherent state input have been performed by assuming that the prepared input state is a pure coherent state. It means 〈δ2X̂in〉 = 〈δ2Ŷin〉 = 1. So equation (14) has become simpler

It agrees with the fidelity given by Furusawa.[14] Equation (15) is very useful in experiments because the fidelity can be calculated directly by the variances of the output state. However, it is only reasonable when the input state is a coherent state. If the input state is a nonclassical state, such as a squeeze state, the fidelity does not work well.[26,27]

The real squeezed input state 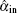suffers from some inevitable losses, mainly in its generation process, having excess noise in the antisqueezing component. Such squeezed states are not pure, but mixed states. This mixed squeezed state is regarded as a squeezed thermal state. Its variances are written as follows:

where 〈δ2X̂p〉 = 〈δ2Ŷp〉 = 1 and coth (2β)/4 is the variance of an initial thermal state. β is the inverse temperature 1/2kBT, where kB is the Boltzmann constant and T is temperature. Accordingly a squeezed thermal state is no longer the minimum-uncertainty state 〈δ2X̂in〉·〈δ2Ŷin〉 > 1. If such a squeezed thermal state is generated as an input of a quantum clone (or quantum teleportation), we can obtain the fidelity by Eq. (13).

3. Fidelity with different inputs

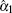
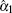
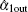
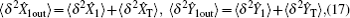
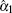
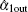
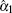
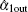
Considering the ideal pure state and the mixed state as the input in the same quantum transport process respectively, with such an input state can we obtain higher fidelity than the other? When the input state is a pure state , the variances of output state is

where 〈δ2X̂1〉 (〈δ2X̂1out〉) and 〈δ2Ŷ1〉 (〈δ2Ŷ1out〉) are the quadrature component variances of the pure input state and output state . 〈δ2X̂T〉 (〈δ2ŶT〉) is inevitable noise induced by the quantum transport process. This inevitable noise is the same for all input states during the same quantum transport process. This is up to the character of the quantum transport process. In unity gains, we do not care about the mean value between the input and output state. We can obtain the fidelity of the pure input state and output state by Eq. (5),

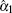
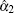
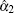
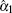
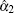
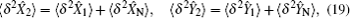
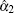
However, in experiments the prepared input state is not always an ideal pure state . It may be a mixed state which named more or less. To compare the fidelity fairly, we assumed the variances of this mixed state are akin to the variances of this pure state in phase space. So we can express the variances of as

where 〈δ2X̂N〉 (〈δ2ŶN〉) is additional noise on the mixed state during the prepared process.

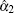
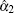
Similarly, when the input state is a mixed state in the same quantum transport process, the variances of the output state are

We can also obtain the fidelity of a mixed state input and output state by Eq. (13).

So we can obtain an inequality by simple calculation

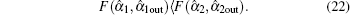
It means the more quantum character the input state has, the lower fidelity we can obtain. That is to say, as the input state varies during the same quantum transport process, it is harder to preserve the quantum character of a pure input state than a mixed input state. This conclusion is suitable for the quantum teleportation (quantum clone).

4. Conclusion

Based on the original definition of fidelity, we give a universal fidelity between two Gaussian mixed states with quantum state quadrature variances. It is convenient to quantify the quantum teleportation (quantum clone) experiment since the variances of the quadrature components of the input and output states are measurable. Furthermore, we also give a conclusion that the fidelity of a pure input state is smaller than the fidelity of a mixed input state in the CV-QIP due to the fragility of the pure state.

Reference
1Wan Z LFan H YWang Z 2015 Chin. Phys. 24 0120301
2Zhang G PZheng K MLiu S YHu L Y 2014 Chin. Phys. 23 050301
3Wu SLiang L MLi C Z 2007 Chin. Phys. 16 1229
4Peters N AWei T CPaul G K 2004 Phys. Rev. 70 052309
5Schumacher B 1995 Phys. Rev. 51 2738
6Jozsa R 1994 J. Mod. Opt. 41 2315
7Uhlmann A 1976 Rep. Math. Phys. 9 273
8Schumacher B 1996 Phys. Rev. 54 2614
9Braunstein S LFuchs C AKimble H J 2000 J. Mod. Opt. 47 267
10Braunstein S LFuchs C AKimble H JLoock P V 2001 Phys. Rev. 64 022321
11Hammerer KWolf M MPolzik E SCirac J I 2005 Phys. Rev. Lett. 94 150503
12Ban M 2004 Phys. Rev. 69 054304
13Grosshans FGrangier P 2001 Phys. Rev. 64 010301
14Furusawa ASrensen J LBraunstein S LFuchs C AKimble H JPolzik E S 1998 Science 282 706
15Aharonov YAlbert D 1981 Phys. Rev. 24 359
16Grangier PGrosshans F2001e-print quant-ph/0010107
17Zhang H LLiang W DLiu KZhang J XGao J R 2012 J. Phys. B: At. Mol. Opt. Phys. 45 115501
18Bowen W PTreps NBuchler B CSchnabel RRalph T CBachor H A 2003 Phys. Rev. 67 032302
19Zhang T CGoh K WChou C WLodahl PKimble H J 2003 Phys. Rev. 67 033802
20Zhai Z HLi Y MWang S KGuo JZhang T CGao J R2005Acta Phys. Sin.542710(in Chinese)
21Takei NYonezawa HAoki TFurusawa A 2005 Phys. Rev. Lett. 94 220502
22Jia X JSu X LPan QGao J RXie C DPeng K C 2004 Phys. Rev. Lett. 93 250503
23Glöckl OLorenz SMarquardt CHeersink JBrownnutt MSilberhorn CPan QLoock P VKorolkova NLeuchs G 2003 Phys. Rev. 68 012319
24Lee NBenichi HTakeno YTakeda SWebb JHuntington EFurusawa A 2011 Science 332 330
25Andersen U LJosse VLeuchs G 2005 Phys. Rev. Lett. 94 240503
26Takei NAoki TKoike SYoshino KWakui KYonezawa HHiraoka TMizuno JTakeoka MBan MFurusawa A 2005 Phys. Rev. 72 042304
27Mista LFilip RFurusawa A 2010 Phys. Rev. 82 012322