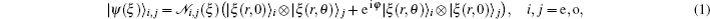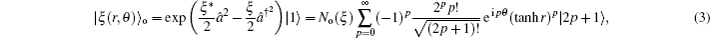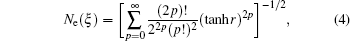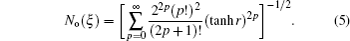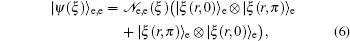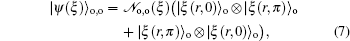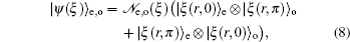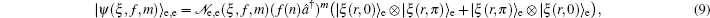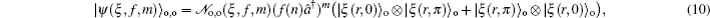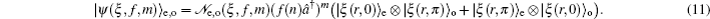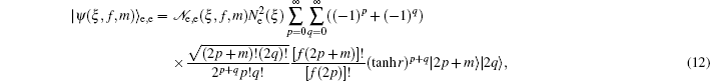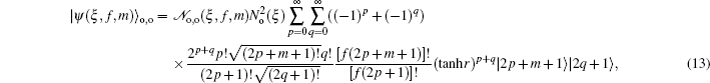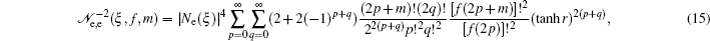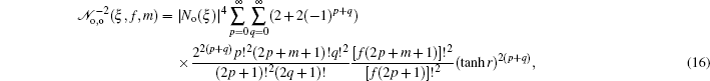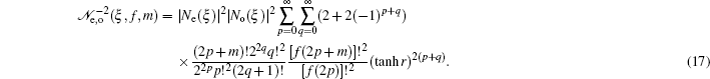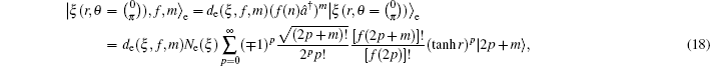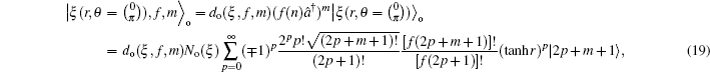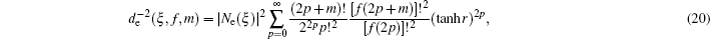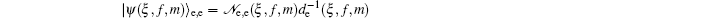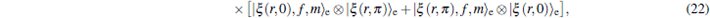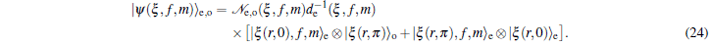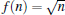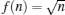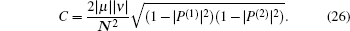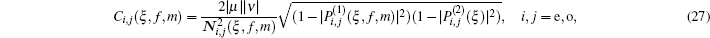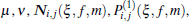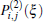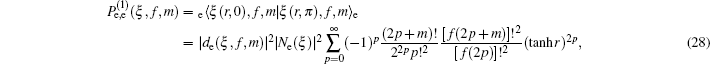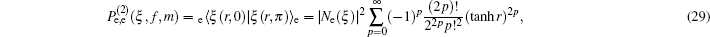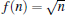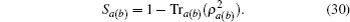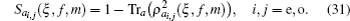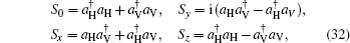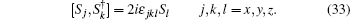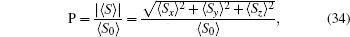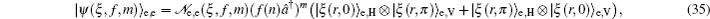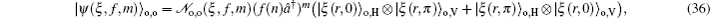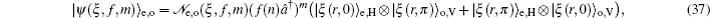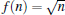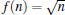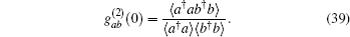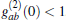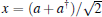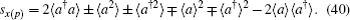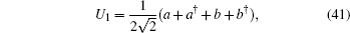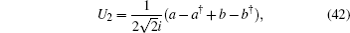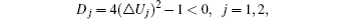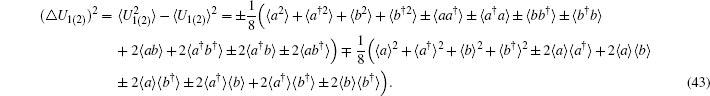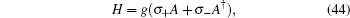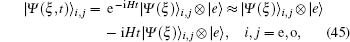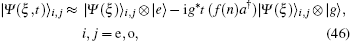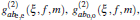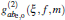Cite this Article
Karimi A, Tavassoly M K. Deformed photon-added entangled squeezed vacuum and one-photon states: Entanglement, polarization, and nonclassical properties. Chinese Physics B, 2016, 25(4): 040303  
Permissions
Deformed photon-added entangled squeezed vacuum and one-photon states: Entanglement, polarization, and nonclassical properties
Karimi A1, 3, †, , Tavassoly M K1, 2, ‡,
Atomic and Molecular Group, Faculty of Physics, Yazd University, Yazd, Iran
The Laboratory of Quantum Information Processing, Yazd University, Yazd, Iran
Physics Group, Islamic Azad University of Abadeh, Fars, Iran

 

† Corresponding author. E-mail: amirkarimi.phy@stu.yazd.ac.ir

‡ Corresponding author. E-mail: mktavassoly@yazd.ac.ir

Abstract
Abstract

In this paper, after a brief review on the entangled squeezed states, we produce a new class of the continuous-variable-type entangled states, namely, deformed photon-added entangled squeezed states. These states are obtained via the iterated action of the f-deformed creation operator A = f (n)a† on the entangled squeezed states. In the continuation, by studying the criteria such as the degree of entanglement, quantum polarization as well as sub-Poissonian photon statistics, the two-mode correlation function, one-mode and two-mode squeezing, we investigate the nonclassical behaviors of the introduced states in detail by choosing a particular f-deformation function. It is revealed that the above-mentioned physical properties can be affected and so may be tuned by justifying the excitation number, after choosing a nonlinearity function. Finally, to generate the introduced states, we propose a theoretical scheme using the nonlinear Jaynes–Cummings model.

PACS: 03.67.Bg;42.50.Dv;42.50.–p
Keyword:squeezed states;deformed photon-added entangled states;entanglement;quantum polarization
1. Introduction

In recent decades, entanglement[1] is known as a favorite characteristic that distinguishes quantum mechanics from classical mechanics. The concept of entanglement plays an important role in the fields of quantum information processing including quantum teleportation,[2] cryptography,[3] and computation,[4] both theoretically and experimentally. Recently, various types of entangled coherent states as one of the entangled continuous-variable-type states have been discussed and different schemes to generate such states have been introduced.[5–9] In this regard, a new class of nonlinear excited entangled coherent states have been introduced and generated by us[10] based on the f-deformed coherent states.[11]

The increasing interest in achieving new quantum states with different nonclassical behaviors motivates researchers to introduce other types of entangled continuous-variable-type states, namely “entangled squeezed states”, and to propose many schemes to generate these states.[12,13] The entangled squeezed states have been produced by using a squeezed state instead of a coherent state in “entangled coherent states”.[14–16] The squeezed states were first formulated mathematically by Stoler[17,18] and then have been observed experimentally by Slusher et al.[19] In some of their applications one may refer to high quality optical communication,[20,21] interferometric technique to detect very weak forces[22] such as gravitational wave detection,[23] optical wave-guide tap,[24] optical sensors[25], computing,[26] and so on.

In addition to entanglement, quantum polarization has also attracted a great deal of attention in recent years due to its key role in many experiments and demonstrations in quantum optics.[27–35] In 1852, Stokes, in his seminal work, first discussed the concept of light polarization. The polarization of light is referred to as the property where the tip of the electric field vector describes an ellipse in the plane transverse to the propagating direction at a fixed space point.[36] In this regard, a polarized light can be used as an excellent information carrier which retains coded information relatively intact on propagation.

On the other hand, Glauber coherent states were introduced in 1963,[37] the photon-added coherent states were introduced by Agarwal and Tara in 1991[38] and then they were generated experimentally by Zavatta et al. in 2005.[39] In this regard, recently the deformed photon-added coherent states were introduced by one of us and their nonclassical properties were considered.[40] Keeping in mind the three steps in the latter-mentioned research procedure, and the fact that we have recently introduced and generated the photon-added entangled squeezed states and studied their properties in Ref. [41], in this paper we aim to introduce a new class of entangled quantum states, namely the deformed photon-added entangled squeezed states. It is worth mentioning that for the squeezed states we will consider the vacuum and the one-photon squeezed states (see Eqs. (2) and (3) of the paper). The introduced states can be obtained via the iterated action (m times) of the f-deformed creation operator A† = f (n)a† on the first mode of the entangled squeezed states. Next, some of the nonclassical properties of the produced states such as entanglement, quantum polarization, sub-Poissonian photon statistics, correlation function and one-mode quadrature squeezing are studied by choosing a particular nonlinearity function, numerically. Moreover, a simple scheme based on the atom-field interaction using the generalized (nonlinear) Jaynes–Cummings model[42,43] for the generation of the introduced entangled states is proposed. In particular, the investigation about the influence of the photon number excitation on the entanglement, polarization and other nonclassicality features of the introduced states motivates us to pay attention to the present contribution. At last, for more physical realization of this study we illustrate a simple theoretical implementation for the generation of the outlined states by using the nonlinear Jaynes–Cummings model.

The paper is organized as follows. In the next section, we present the explicit form of entangled squeezed states. In Section 3, we introduce deformed photon-added entangled squeezed states. Next, we pay attention to the entanglement and quantum polarization of the introduced states, in Sections 4 and 5, respectively. Section 6 deals with a few other nonclassicality features in detail. A theoretical scheme for the generation of the introduced states has been proposed in Section 7 and finally, we present a summary and concluding remarks in Section 8.

2. Entangled squeezed states: a brief review

At first, based on the introduced entangled coherent states in the literatures[9] we have recently defined the two-mode entangled squeezed states generally in the following form[40]

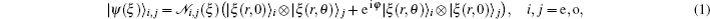
where 𝒩i,j(ξ) is the normalization coefficient. The subscripts e and o in Eq. (1) refer to even and odd squeezed states, namely squeezed vacuum and squeezed one-photon states, respectively[44]

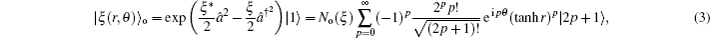
where â and ↠are the bosonic annihilation and creation operators, respectively and ξ = reiθ is a complex parameter. The normalization coefficients Ne(ξ) and No(ξ) may be obtained as:

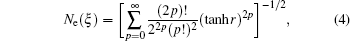
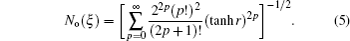
As is seen, various entangled squeezed states can be obtained by choosing different values of phase differences between the two modes of the field θ and between the two components of the entangled squeezed states φ. In this paper, by setting the phase differences θ = π and φ = 0, we introduce three different entangled squeezed states (even–even, odd–odd, and even–odd) as follows:

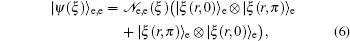
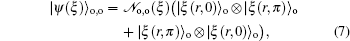
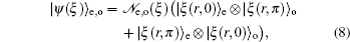
where |ξ(r,0)〉e and |ξ(r,π)〉e (|ξ(r,0)〉o and |ξ(r,π)〉o) have been introduced in Eq. (2) (Eq. (3)). Clearly, 𝒩e,e(ξ), 𝒩o,o(ξ), and 𝒩e,o(ξ) are appropriate normalization factors which can be easily determined.

It is worth mentioning that the first and second modes in the two-mode entangled squeezed states given by Eq. (1) will be denoted with modes a and b, respectively.

3. Deformed photon-added entangled squeezed states

Now, we introduce the deformed photon-added entangled squeezed states that may be produced by the iterated action of the deformed creation operator f (n)a† on the first mode of the two-mode entangled squeezed states in Eq. (1). So, we can define three distinct classes of deformed photon-added entangled squeezed states corresponding to the presented entangled squeezed states in Eqs. (6), (7), and (8) in the following forms:

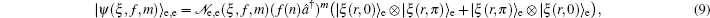
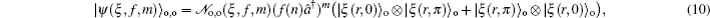
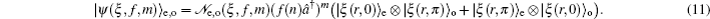
Using the even and odd squeezed state in Eqs. (2) and (3), the number bases representations of the above introduced states can be derived as:

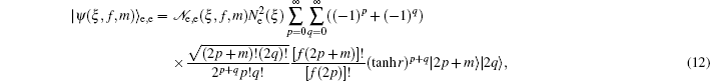
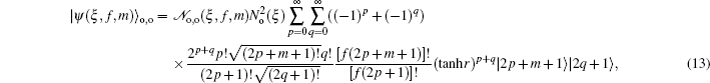
where the normalization constants can be deduced as follows:

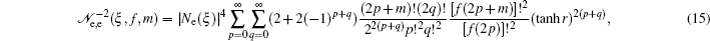
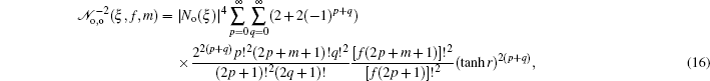
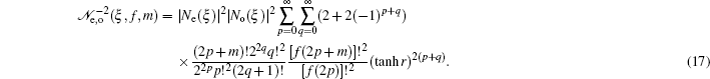
In order to obtain the explicit form of the introduced states in Eqs. (9)–(11), at first we respectively define the photon-added even and odd squeezed states by making use of Eqs. (2) and (3) with θ = 0, π, as follows:

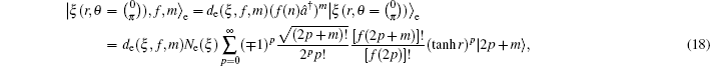
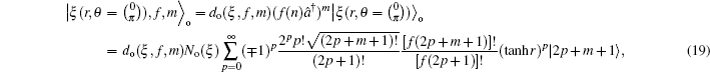
where the normalization coefficients de(ξ, f, m) and do(ξ, f, m) are determined as follows:

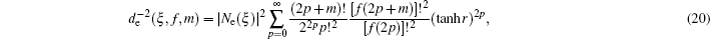
where the coefficients Ne(ξ) and No(ξ) have been obtained in Eqs. (4) and (5), respectively. By using Eqs. (18) and (19), we can respectively rewrite Eqs. (9), (10), and (11) in the following forms:

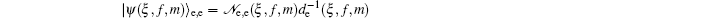
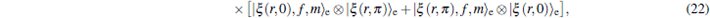
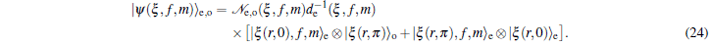
By setting f (n) = 1 in Eqs. (22)–(24) one is led to the photon-added entangled squeezed states which recently have been introduced by us and their nonclassical properties have been studied.[41] Clearly, various classes of deformed photon-added entangled squeezed states can be achieved by choosing the well-known nonlinearity functions f (n) corresponding to different nonlinear quantum systems with various nonclassicality features and different physical properties.

In this contribution, as a physical realization of the presented formalism, we will choose the nonlinearity function 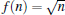which is frequently used by the authors who have worked in the framework of the nonlinear regime of atom-field interactions.[40,45,46] This function also arises in a natural way in the Hamiltonian illustrating the interaction with intensity-dependent coupling between a two-level atom and an electromagnetic radiation field.[46–48] In particular, Fink et al. have explored a natural way in which this nonlinearity function will appear in physical systems.[49] Henceforth, we are ready to produce the introduced entangled states corresponding to this particular nonlinearity function and investigate their physical behavior.

4. Degree of entanglement of the introduced states

In this section we evaluate the amount of entanglement of the deformed photon-added entangled squeezed states by studying two measures, i.e., ‘concurrence’ and ‘linear entropy’. In this way, we will consider the entanglement of the introduced entangled states to photon excitations for the particular nonlinearity function .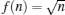

4.1. Concurrence

To measure the degree of quantum entanglement of any two-mode entangled states we can use the concurrence which is generally defined for discrete-variable entangled states as:[50] C = |〈Ψ|σy ⊗ σy|Ψ*〉|, where |Ψ*〉 is the complex conjugate of |Ψ〉. The value of this criterion gets 1 for a maximally entangled state. As is clear from Eqs. (22), (23), and (24), the deformed photon-added entangled squeezed states are two component entangled states. In order to consider the concurrence of our introduced continuous-variable-type entangled states, one can suppose a general bipartite entangled state in the following form:

where |η〉 and |ξ〉 (|γ〉 and |δ〉) are normalized states of subsystem a (subsystem b) with complex numbers μ and ν. The normalization coefficient is given by: N2 = |μ|2 + |ν|2 + 2Re(μ*ν P(1) P(2)*) where P(1) = 〈η|ξ〉 and P(2) = 〈δ|γ〉.

By transforming the continuous-variable-type components to the discrete orthogonal bases and by making use of the Schmidt decomposition,[51,52] the concurrence of the introduced entangled continuous-variable-type states in Eqs. (22)–(24) has been given in the following form[50,53,54]

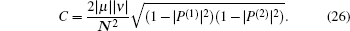
By comparing our introduced states (Eqs. (22)–(24)) in the previous section with the general state in Eq. (25) we find that they are in a similar pattern. Therefore, with the help of Eqs. (25) and (26) we can calculate the concurrence of the three deformed photon-added entangled squeezed states (9), (10), and (11) as:

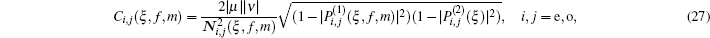
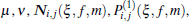
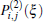
where by comparing the relations (25) with Eqs. (22), (23), and (24), the parameters and distinguished. As an example, for the calculation of Ce,e(ξ, f, m), i.e., the concurrence of the deformed photon-added even-even entangled squeezed states in Eq. (9) by using Eq. (22), we see that μ = 1, ν = 1, and finally,

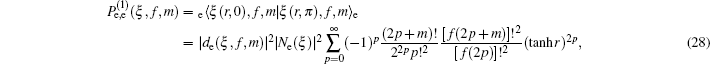
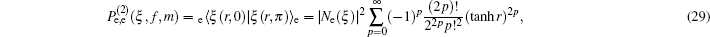
in which Ne(ξ), 𝒩e,e(ξ, f, m), and de(ξ, f, m) have been introduced in Eqs. (4), (15), and (20), respectively. By inserting all these quantities in Eq. (27), one is led to Ce,e(ξ, f, m).

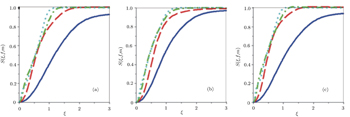
After performing all the necessary calculations, we have plotted the concurrence of the deformed photon-added entangled squeezed states versus |ξ | for the nonlinearity function 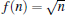in Fig. 1 for different numbers of photon excitations, m.

Fig. 1. The concurrence Ce,e(ξ, f, m), Co,o(ξ, f, m), and Ce,o(ξ, f, m) of the deformed photon-added entangled squeezed states versus |ξ | for the different photon excitations m = 0 (solid), m = 1 (dash), m = 3 (dash–dot), and m = 5 (dot) in panels (a), (b), and (c), respectively.

It can be seen from Figs. 1(a), 1(b), and 1(c) that Ce,e(ξ, f, m), Co,o(ξ, f, m), and Ce,o(ξ, f, m), the concurrence of the even–even, odd–odd, and even–odd deformed photon-added entangled squeezed states corresponding to |ψ(ξ, f, m)〉e,e, |ψ(ξ, f, m)〉o,o, and |ψ(ξ, f, m)〉e,o, have generally the same behavior. After starting from zero, they grow up by increasing |ξ | for all of the photon number excitations, m, and finally tend to 1 in the region of a strong field. Also, the rate of growing the concurrence by increasing the number of photon excitations, m is more rapid in the region of a weak field.

4.2. Linear entropy

As another measure of entanglement, we calculate the linear entropy of the introduced entangled states which is defined for a bipartite state in the following form[55–57]

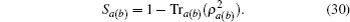
In this relation, ρa(b) is the reduced density operator of the density operator ρab = |ψ〉ab ab〈ψ| where |ψ〉ab is one of the entangled squeezed states introduced in Eqs. (22), (23), and (24) with a,b = e,o. Finally, by using Eq. (30) the linear entropies Sai,j(ξ, f, m) of the first mode, a of the introduced states are obtained as:

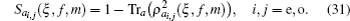
We plotted the linear entropies of the deformed photon-added entangled squeezed states versus |ξ | in Fig. 2 for different numbers of photon excitations, m.

Fig. 2. The linear entropy Sae,e(ξ, f, m), Sao,o(ξ, f, m), and Sae,o(ξ, f, m) of the deformed photon-added entangled squeezed states versus |ξ | for the different photon excitations m = 0 (solid), m = 1 (dash), m = 3 (dash–dot), and m = 5 (dot) in panels (a), (b), and (c), respectively.

As is clear from this figure, the linear entropies Sai,j(ξ, f, m) of the introduced states for each of the entangled states (even–even, odd–odd, and even–odd) have qualitatively the same behaviour as the concurrence.

5. Quantum polarization

In this section, we study the quantum polarization of the deformed photon-added entangled squeezed states by evaluating the Stokes operators. These operators are introduced in the following form[58]

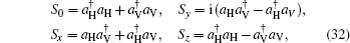
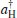
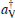
in which aH and (aV and ) are the annihilation and creation operators corresponding to the horizontal (vertical) component of any two-mode quantum state. Interestingly, the latter operators satisfy the commutation relations of the well-known SU(2) group:

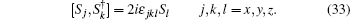
By making use of the above-mentioned Stokes operators, the quantity of quantum polarization is defined in the following form[59]

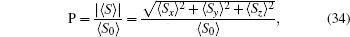
which its value varies between 0 (complete unpolarized states) and 1 (complete polarized states).

To study the quantum polarization of the introduced entangled states in (9)–(11), we present these states respectively in the new forms as:

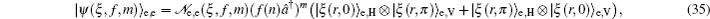
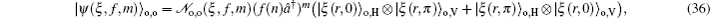
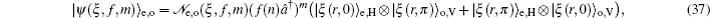
in which the subscripts H and V are referred to as horizontal and vertical components of the introduced states, respectively. By these explanations, we suppose here the first and second modes of the field respectively in the horizontal and vertical polarization.

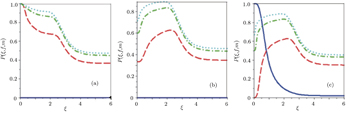
After doing all the necessary calculations (not shown here), we have plotted the quantum polarization of the deformed photon-added entangled squeezed states versus |ξ | by choosing the nonlinearity function 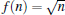for a different number of photon excitations m in Fig. 3.

Fig. 3. The quantum polarization Pe,e(ξ, f, m), Po,o(ξ, f, m), and Pe,o(ξ, f, m) of the deformed photon-added entangled squeezed states versus |ξ | for the different photon excitations m = 0 (solid), m = 1 (dash), m = 3 (dash–dot), and m = 5 (dot) in panels (a), (b), and (c), respectively.

As is observed from this figure, the even–even and odd–odd entangled squeezed states (m = 0) are complete unpolarized states, while the even–odd entangled squeezed state (m = 0) is a complete polarized state in the region of weak fields. Its polarization starts from 1 and suddenly decreases by increasing r and finally tends to 0.

The polarization of the even–even deformed photon-added entangled squeezed states (Fig. 3(a)) for all of the photon excitations, m starts from 1 and after two decrements in the medium region of fields remains fixed about P = 0.5. The amount of two decrements decreases by increasing the number of photon excitations, m.

In the cases of the odd-odd and even–odd deformed photon-added entangled squeezed states (Figs. 3(b) and 3(c)) similar behaviors are visible. Their polarizations start from nonzero values, increase and then decrease in the mean region of the field and finally remain fixed about P = 0.5. The initial nonzero values of polarization increase by increasing the number of photon excitations, m. Moreover, the initial values of polarization of the odd–odd deformed photon-added entangled squeezed states (Fig. 3(b)) exceed that of the deformed photon-added even–odd entangled squeezed states (Fig. 3(c)).

6. Other nonclassical properties of the introduced states

In this section, we intend to evaluate some other nonclassical features of the introduced states in Section 3. To achieve this purpose, we pay attention to a few important nonclassicality criteria such as “sub-Poissonian statistics”, “second-order correlation function”, “one-mode squeezing”, and “two-mode squeezing”.

6.1. Quantum statistics

To investigate the quantum statistics of any quantum state, as is usual, we consider the Mandel parameter[60] which is defined for each mode as

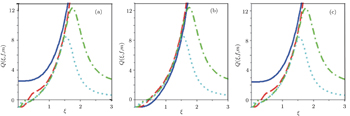
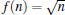
The super- and sub-Poissonian photon statistics correspond respectively to Qi > 0 and Qi < 0.[61] The negativity of Q indicates the nonclassicality of the state.[61] We have plotted the Mandel parameters of the first mode, a, of the deformed photon-added entangled squeezed states versus |ξ | for a particular nonlinearity function in Fig. 4 for different numbers of photon excitations, m. As is clear from this figure, the sub-Poissonian photon statistics appear in all three cases of the even–even, odd–odd, and even–odd deformed photon-added entangled squeezed states (|ψ(ξ, f, m)〉e,e, |ψ(ξ, f, m)〉o,o, and |ψ(ξ, f, m)〉e,o) for all of the numbers of photon excitations and over all of the regions of the field except the region of medium intensities of the field. This region becomes narrower by increasing the number of photon excitations. Also, only in the odd–odd entangled squeezed state, |ψ(ξ,0)〉o,o, the sub-Poissonian photon statistics are seen in the region of the weak field, while the even–even and even–odd entangled squeezed states, |ψ(ξ,0)〉e,e and |ψ(ξ,0)〉e,o, have no sub-Poissonian photon statistics.

Fig. 4. The Mandel parameter Qae,e(ξ, f, m), Qao,o(ξ, f, m), and Qae,o(ξ, f, m) of the deformed photon-added entangled squeezed states versus |ξ | for the different photon excitations m = 0 (solid), m = 1 (dash), m = 3 (dash–dot), and m = 5 (dot) in panels (a), (b), and (c), respectively.
6.2. Two-mode correlation degree

In this subsection, we consider the second-order correlation degree of the two modes of the introduced states by calculating the second-order cross-correlation function which has been defined as[62]

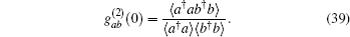
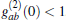
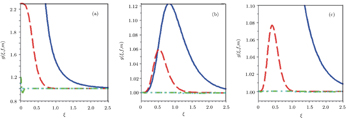
A state is nonclassical, if .[63] We have plotted the second-order correlation function between the two modes of the deformed photon-added entangled squeezed states versus |ξ | for different numbers of photon excitations in Fig. 5. It can be seen that only the even–even deformed photon-added entangled squeezed states for m > 1 show this nonclassicality sign in the region of the weak field.

Fig. 5. The second-order correlation function and of the deformed photon-added entangled squeezed states versus |ξ | for different photon excitations m = 0 (solid), m = 1 (dash), m = 3 (dash–dot), and m = 5 (dot) in panels (a), (b), and (c), respectively.
6.3. Squeezing properties
6.3.1. One-mode squeezing

In order to calculate the quadratures squeezing of the introduced entangled states, we consider two Hermitian operators 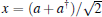and with commutation relation [x,p] = i. Accordingly, the following parameters for quadrature squeezing in x and p may be defined as sxj = 2(Δxj)2 − 1, (xj = x,p) or equivalently

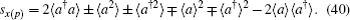
A state is squeezed in xj = x or p if it satisfies the inequality −1 < sxj < 0.

In order to observe the squeezing in one of the field quadratures corresponding to one of the two modes of the deformed photon-added entangled squeezed states, we have plotted the x- and p-squeezing parameters for the first mode (a) of the introduced states versus |ξ |. By plotting the figures we observed that no squeezing occurs for the introduced entangled squeezed states for all of the photon number excitations (the figure not shown here).

6.3.2. Two-mode squeezing

As another indicator to analyze the quantum fluctuations of any two-mode entangled state, two hermitian parameters are defined as follows:[64]

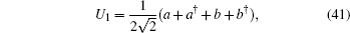
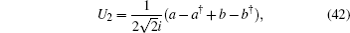
which satisfy the commutation relation [U1, U2] = i/2. The following parameters for two-mode squeezing in U1 and U2 can be defined as

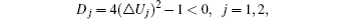
where

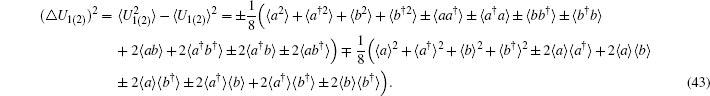
In this case, also no two-mode quadrature squeezing was found for the introduced entangled states (the figure not shown here).

7. Generation of the deformed photon-added entangled states

After constructing and studying some of the nonclassical properties of the “deformed photon-added entangled squeezed states” in the previous sections, now we propose a theoretical scheme to generate such states in experiment. In what follows, we present a theoretical scheme based on a proposal for the interaction of a two-level atom with a two-mode quantized field.

The atom emits a photon by making a transition from the excited state |e〉 to the ground state |g〉. Based on the nonlinear Jaynes–Cummings model of atom-field interaction,[42,43,65–67] the Hamiltonian of the atom–field system in the RWA and resonant condition is given by:[42]

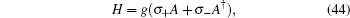
where g is the atom–field coupling constant, σ+ = |e〉〈g| and σ− = |g〉〈e| are the Pauli atomic operators and A = af(n) and A† = f (n)a† are the deformed annihilation and creation operators, respectively. Clearly, it can be observed that we deal with a generalization of the Hamiltonian in the standard JCM Hamiltonian H = g(σ+a + σ− a†) which is related to the resonant interaction between a two-level atom with a single-mode quantized field in the dipole approximation and with the rotating wave approximation. By referring to the literature which is concerned with intensity-dependent (nonlinear) JCM,[68–77] it can be clearly found that in the above Hamiltonian (44) the atom–field coupling constant is simply transformed to the intensity-dependent coupling (i.e., g = gf (n)).

By assuming that the atom is initially in the excited state |e〉 and the field in each of the introduced entangled squeezed states in Eqs. (6)–(8), the state of the atom–field system after the time t, in the case of the weak coupling constant g, can be obtained as follows:

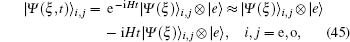
which is valid for gt ≪ 1 (recall that two generation schemes for the entangled squeezed states introduced in Eqs. (6)–(8) have been proposed in Refs. [12] and [13]). By using (44), we can rewrite (45) in the following form:

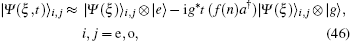
which clearly indicates that, if one detects the atom in the ground state |g〉, the state of the field is collapsed to the deformed photon-added entangled squeezed states |Ψ(ξ,f,1)〉i,j in Eqs. (9), (10), and (11) with m = 1.

Using the above scheme, the introduced deformed photon-added entangled squeezed states in Eqs. (9)–(11) can be generated by passing m(>1) successive atoms through the cavity and detecting all of them in the ground state |g〉. In another way, by supposing the multi-photon medium (for a two-photon medium see Ref. [78]) which has been introduced in the literature as:[66,69,79–83]

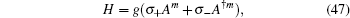
the multi-photon deformed photon-added entangled squeezed states for arbitrary values of m, can be generated. In a similar manner which we followed in Eq. (45), for the latter case one arrives at

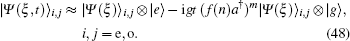
By detecting the atom in the ground state |g〉 in the interaction process expressed via Eq. (48) one immediately arrives at the introduced deformed photon-added entangled squeezed states in the paper.

8. Summary and conclusion

In this paper, at first we had a brief review on general types of two-mode entangled quantum states namely “even–even, odd–odd, and even–odd entangled squeezed states” (|ψ(ξ)〉i,j, i,j = e,o) which are constructed by replacing the coherent states in the previously introduced entangled coherent states[9] with the (even and odd) squeezed states. Then, we introduced the corresponding “deformed photon-added entangled squeezed states” |ψ(ξ, f, m)〉i,j via the iterated action of the deformed creation operator f (n)a† on the first mode of each of the two-mode entangled squeezed states. In the continuation, after deriving the explicit forms of the introduced states in the number states, we studied the amount of entanglement and quantum polarization of the entangled states, numerically. Also, we discussed some of the nonclassicality criteria such as: the Mandel parameter, second-order correlation function, one-mode and two-mode quadrature squeezing. In particular, we investigated the influence of the photon number excitation on the considered criteria. Finally, we presented a theoretical scheme to generate the introduced states. The obtained numerical results are briefly shown as follows.

Reference
1Horodecki RHorodecki PHorodecki MHorodecki K 2009 Rev. Mod. Phys. 81 865
2Bennett C HBrassard GCréeau CJozsa RPeres AWootters W K 1993 Phys. Rev. Lett. 70 1895
3Ekert A 1991 Phys. Rev. Lett. 67 661
4Barenco ADutch DEkert AJozsa R 1995 Phys. Rev. Lett. 74 4083
5Bužek VBarranco A VKnight P L 1992 Phys. Rev. 45 6570
6Donodov V VMalkin I AMan’ko V I 1974 Physica 72 597
7Yurke BStoler D 1986 Phys. Rev. Lett. 57 13
8Sanders B C 1992 Phys. Rev. 45 6811
9Yurke BStoler D 1987 Phys. Rev. 35 4846
10Karimi ATavassoly M K 2015 Phys. Scr. 90 015101
11de Matos Filho R LVogel W 1996 Phys. Rev. 54 4560
12Zhang Z MYang JYu Y F 2007 Chin. Phys. Lett. 24 352
13Kuanga L MZeng A HKuang Z H 2003 Phys. Lett. 319 24
14Barnett S MKnight P L 1985 J. Opt. Soc. Am. 2 467
15Barnett S MKnight P L 1987 J. Mod. Opt. 34 841
16Hong-yi F 1990 Phys. Rev. 41 1526
17Stoler D1970Phys. Rev. D13217
18Stoler D 1971 Phys. Rev. 4 1935
19Slusher R EHollberg L WYurke BMertz J CValleySlusher J F 1985 Phys. Rev. Lett. 55 2409
20Wang JSui QWang C 1995 Quantum Semiclass. Opt. 7 917
21Zhao L HYang Z YZhang Z JHou X2000Acta Photon. Sin.29193
22Hou YMeng J DTian L KHu Y FWan YYang Z Y2001Acta Photon. Sin.301194
23Ming C SXu D GAn Y Y2002Acta Photon. Sin.31412
24Shapiro J H 1980 Opt. Lett. 5 351
25Righini G CTajani ACutolo A2009An Introduction to Optoelectronic SensorsSingaporeWorld Scientific
26Caves C M 1981 Phys. Rev. 23 1693
27Bennett C HBessette FBrassard GSalvail LSmolin J A1992J. Cryptology53
28Muller ABreguet JGisin N 1993 Europhys. Lett. 23 383
29Kwiat P GMattle KWeinfurter HZeilinger ASergienko A VShih Y 1995 Phys. Rev. Lett. 75 4337
30Mattle KWeinfurter HKwiat P GZeilinger A 1996 Phys. Rev. Lett. 76 4656
31Bouwmeester DPan J WMattle KEibl MWeinfurter HZeilinger A 1997 Nature 390 575
32Luis A 2002 Phys. Rev. 66 013806
33Barbieri MDe Martini FDi Nepi GMataloni PDe Ariano G MMacchiavello C 2003 Phys. Rev. Lett. 91 227901
34Luis A 2005 Phys. Rev. 71 063815
35Luis A 2007 Phys. Rev. 75 053806
36Stokes G G1852Trans. Cambridge Philos. Soc.9399
37Glauber J 1963 Phys. Rev. 131 2766
38Agarwal G STara K 1991 Phys. Rev. 43 492
39Zavatta AViciani SBellini M 2005 Phys. Rev. 72 023820
40Safaeian OTavassoly M K 2011 J. Phys. A: Math. Theor. 44 225301
41Dibakar ETavassoly M Kkarimi A 2015 Phys. Scr. 90 085102
42Jaynes E TCummings F W 1963 Proc. IEEE 51 89
43Cummings F W 1965 Phys. Rev. 140 1051
44Gerry C CKnight P L2005Introductory Quantum OpticsCambridgeCambridge University Press
45Buck BSukumar C V 1981 Phys. Lett. 81 132
46Agarwal G SSingh S 1982 Phys. Rev. 25 3195
47Huang CTang LKong FFang JZhou M 2006 Physica 368 25
48Sukumar C VBuck B 1984 J. Phys. A: Math. Gen. 17 877
49Fink J MGoppl MBaur MBianchetti RLeek P JBlais AWallraff A 2008 Nature 454 315
50Hill SWootters W K 1997 Phys. Rev. Lett. 78 5022
51Mann ASanders B CMunro W J 1995 Phys. Rev. 51 989
52Rungta PBuzék VCaves C MHillery MMilburn G J 2001 Phys. Rev. 64 042315
53Kuang L MZhou L 2003 Phys. Rev. 68 043606
54Wang X G 2002 J. Phys. A: Math. Gen. 35 165
55Bennett C HBernstein H JPopescu SSchumacher B 1996 Phys. Rev. 53 2046
56Agarwal G SBiswas A 2005 J. Opt. B: Quantum Semiclass. Opt. 7 350
57Miry S RTavassoly M K 2012 J. Phys. B: At. Mol. Opt. Phys. 45 175502
58Collett E 1970 Am. J. Phys. 38 563
59Brosseau C1998Fundamentals of Polarized Light: A Statistical Optics ApproachNew YorkWiley
60Mandel L 1979 Opt. Lett. 4 205
61Davidovich L 1996 Rev. Mod. Phys. 68 127
62Paul H 1982 Rev. Mod. Phys. 54 1061
63Song T QFan H Y 2002 J. Phys. A: Math. Gen. 35 1071
64Loudon RKnight P L 1987 J. Mod. Opt. 34 709
65Baghshahi H RTavassoly M KBehjat A 2014 Chin. Phys. 23 074203
66Baghshahi H RTavassoly M KBehjat A 2014 Commun. Theor. Phys. 62 430
67Baghshahi H RTavassoly M K 2015 Eur. Phys. J. Plus 130 37
68Buck BSukumar C V 1981 Phys. Lett. 81 132
69Sukumar C VBuck B 1981 Phys. Lett. 83 211
70Buek V 1989 Phys. Rev. 39 3196
71Singh SudhaReimond Ooi C HAmrita 2012 Phys. Rev. 86 023810
72Gora PJedrzejek C 1992 Phys. Rev. 45 6816
73Klimov A BChumakov S M2009A Group-Theoretical Approach to Quantum OpticsCambridgeCambridge University Press
74Rastegarzadeh MTavassoly M K 2015 Phys. Scr. 90 025103
75Naderi M HSoltanolkotabi MRoknizadeh R 2005 Eur. Phys. J. 32 397
76Yadollahi FTavassoly M K 2011 Opt. Commun. 284 608
77Yadollahi FTavassoly M K 2012 Int. J. Mod. Phys. 26 1250027
78Davidovich LRaimond J MBrune MHaroche S 1987 Phys. Rev. 36 3771
79Sing S 1982 Phys. Rev. 25 3206
80Font J LFernádez-Soler J JVilaseca RGauthier D J 2005 Phys. Rev. 72 063810
81Shore B WKnight P L 1993 J. Mod. Opt. 40 1195
82Baghshahi H RTavassoly M KBehjat A 2014 Chin. Phys. 23 074203
83Baghshahi H RTavassoly M KBehjat A 2014 Commun. Theor. Phys. 62 430