† Corresponding author. E-mail:
The Shannon information entropy is investigated within the nonrelativistic framework. The Kratzer potential is considered as the interaction and the problem is solved in a quasi-exact analytical manner to discuss the ground and first excited states. Some interesting features of the information entropy densities as well as the probability densities are demonstrated. The Bialynicki–Birula–Mycielski inequality is also tested and found to hold for these cases.
Interest in the study of wave equations of quantum mechanics has been considerably renewed due to their notable applications in measurement and information technologies. In particular, the entropic uncertainty relations, which provide alternatives to the ordinary Heisenberg uncertainty relation, have been investigated.[1–39] Within the proposed entropies, the Shannon entropy possesses interesting features and is quite an appealing theoretical framework.[1–3] The BBM entropic uncertainty relation, named after Beckner, Bialynicki–Birula, and Mycielski (see, Ref. [4]) is given by
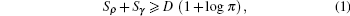

The Shannon entropy has been studied for some quantum systems with exact analytical solutions. Sun et al.[42] applied Shannon information entropies to a position-dependent mass Schrödinger problem with a hyperbolic well. They calculated the position and momentum information entropies for six low-lying states. Some interesting features of the information entropy densities were demonstrated and the BBM inequality was also tested.[42] Yáñez-Navarro et al. have studied quantum information entropies for position-dependent-mass Schrödinger problems and have demonstrated the behaviors of the position and momentum information entropies. They showed the negative Shannon entropy exits for the probability densities that are highly localized and proved that the mass barrier determines the stability of the system.[43] Rudnicki et al. studied the Shannon entropy-based uncertainty relation for D-dimensional central potentials and found that the resulting lower bound does not depend on the specific form of the potential since it only depends on the hyperangular quantum numbers.[44] Song et al. studied the Shannon information entropy for an infinite circular well and tested the validity of the BBM inequality.[45] Sun et al. studied the Shannon information entropy for a hyperbolic double-well potential and calculated the position and momentum information entropies for the lowest-lying states n = 1,2. They also observed that the position information entropy decreases with an increase in the potential strength but the momentum entropy is contrary to the position entropy. They checked the validity of BBM inequality as well.[46] The particle in a symmetrical squared tangent potential and its Shannon information entropy were well analyzed in Ref. [47]. Massen applied Shannon information entropies in position and momentum space to various s–p and s–d shell nuclei using a correlated one-body density matrix and proposed a method to determine the correlation.[48] Lin et al. used Shannon entropy to probe the nature of correlation effects. In addition, they considered the concept in connection with helium-like systems including positronium negative ion, hydrogen negative ion, helium and lithium positive ion.[49] Dehesa et al. explicitly obtained the information entropy for a harmonic oscillator and the hydrogen atom in D dimensions. They showed how these entropies are related to entropies involving polynomials.[50] Dehesa et al. studied the spreading of the quantum-mechanical probability cloud for the ground-state of the Morse and modified Pöschl-Teller potentials by means of global and local information-theoretic measures.[51]
On the other hand the Kratzer potential is amongst the most attractive physical potentials as it contains an inverse square term besides the common Coulomb term which has well accounted for some observed phenomena in atomic, molecular and chemical physics.[52–58] Before focusing on our work, we wish to address the interesting papers[59–68] which discuss various aspects of the field.
The present article is organized as follows. In the next section, we give the quasi-exact solutions of the nonrelativistic Kratzer potential. In the third section, we first derive the wave functions in momentum space via the Fourier transform and then report the position and momentum information entropy densities, ρs (
For an arbitrary external potential V(r), the Schrödinger equation in spherical coordinates is written as
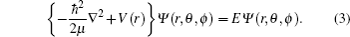

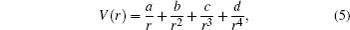
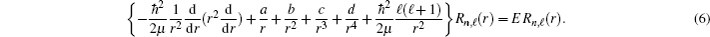
The transformation
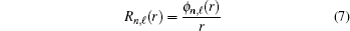
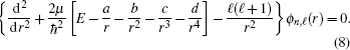

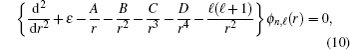

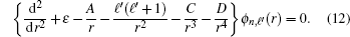
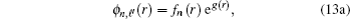
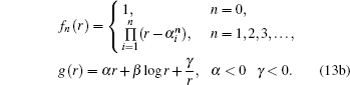
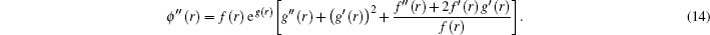

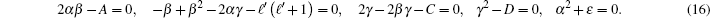
Therefore, we find restrictions on potential parameters as

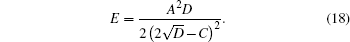
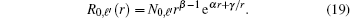



The position and momentum space information entropies for three-dimensional potentials can be calculated using Eq. (
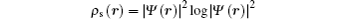
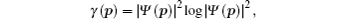
Owing to the difficulty in calculating wave functions in momentum space, we only consider the lowest states n = 1. For simplicity, we study the n = 1 case in more detail. For the Fourier transform of n = 1 we only list the main results in Table
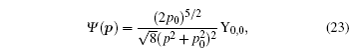
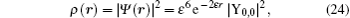

| Table 1. Information entropies of the n = 1 eigenstates for ℓ′ = 0. . |
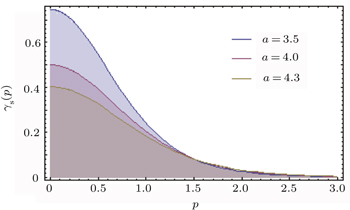
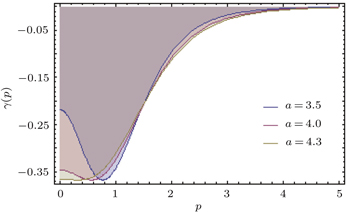
In Figs.
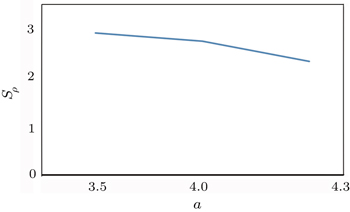
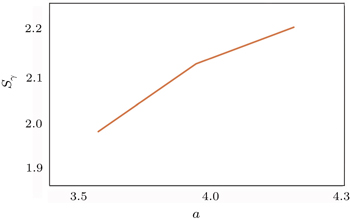
In Table
We present the Shannon entropy for the position and momentum eigenstates of the Schrödinger equation with the Kratzer potential. The position Sρ and momentum Sγ information entropies are calculated for n = 1. Particularly, the Sρ entropy for the lowest state is derived analytically, and also some numerical calculations for Sγ are presented. We find that the position information entropy Sρ decreases with the increase of parameter a, but the behavior of Sγ is contrary to that of the Sρ. The influence of parameter a on the stability of the system is shown in detail. Some interesting features of the information entropy densities, ρs (
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 | |
| 47 | |
| 48 | |
| 49 | |
| 50 | |
| 51 | |
| 52 | |
| 53 | |
| 54 | |
| 55 | |
| 56 | |
| 57 | |
| 58 | |
| 59 | |
| 60 | |
| 61 | |
| 62 | |
| 63 | |
| 64 | |
| 65 | |
| 66 | |
| 67 | |
| 68 | |
| 69 | |
| 70 | |
| 71 |